記事監修：小田井　英陽
（一般社団法人日本官能評価学会理事、東京バイオテクノロジー専門学校講師）

• PLS回帰とは？
• PLS回帰を実行するためのデータセット
• PLS回帰を実行する手順
• 出力結果の解釈
• 分析結果のまとめ
• まとめ
• 参考文献
• XLSTAT の無料トライアル

PLS回帰とは？

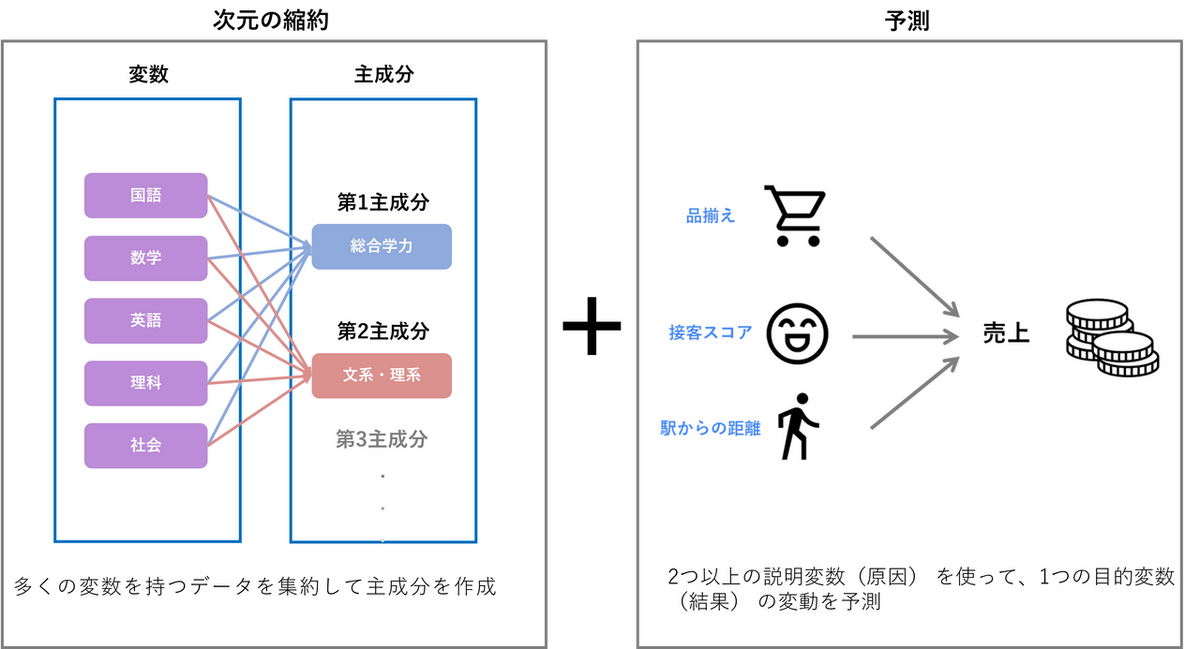
PLS（Partial Least Squares：部分的最小二乗）回帰は、回帰分析の一種であり、主成分分析（PCA）のような「次元の縮約」と、重回帰分析のような「予測」の特性を組み合わせた統計手法です。PCA とPLS が異なるのは、潜在変数の作り方で、PCA は説明変数だけを考慮するのに対して、PLS は説明変数と目的変数の両方を考慮するため、回帰手法として優れています。また、PLS は通常の重回帰分析と比較して、主に4つの大きな強みがあります。

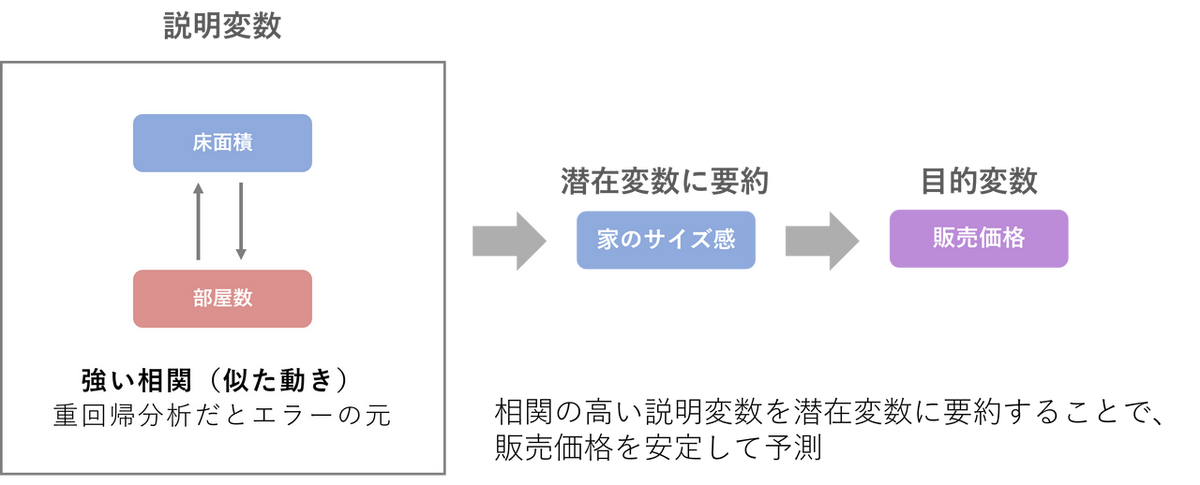
1. 「似たような変数（多重共線性）」に強い

通常の重回帰分析では、説明変数間に強い相関（多重共線性）があると計算が不安定になります。例えば、「家のスペック（説明変数）から販売価格（目的変数）を予測する」ケースを考えてみましょう。説明変数に「床面積」と「部屋数」がある場合、これらは通常、家が大きければ部屋数も増えるため、データとして非常に似た動きをします（強い相関）。重回帰分析では、このように似たような変数が複数あると、それぞれが独立した要因としてうまく機能せず、予測モデルが破綻してしまいます。PLS回帰では、上記のような相関の高い変数群を「家のサイズ感」のような成分（潜在変数）に要約してから分析するため、相関が高い変数が多くても安定したモデルを作成することができます。

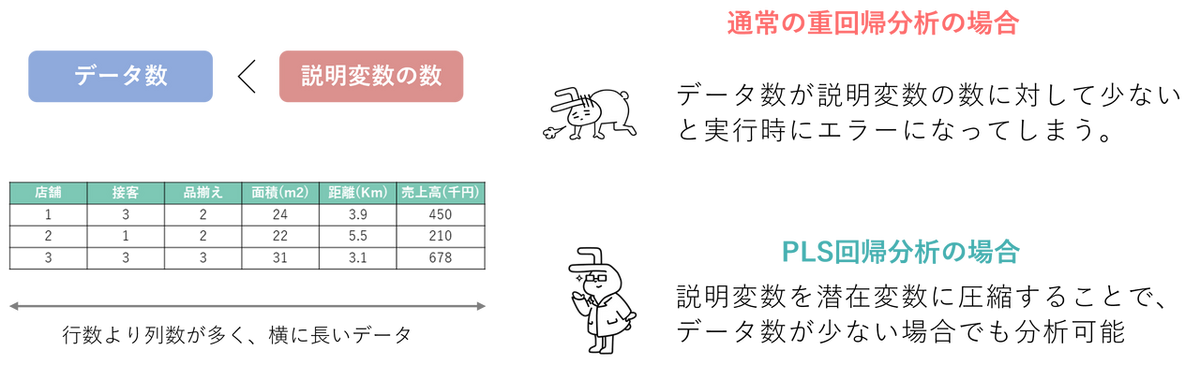
2. 「観測数（サンプル）より変数の数が多い」データでも分析できる

通常の重回帰分析は、数学的な仕組み上、「データの数（行）」よりも「変数の数（列）」の方が多いと計算ができません（エラーになります）。 しかし、PLS回帰は変数を少数の「成分」に要約してから計算するため、下記の横長の表のように、サンプル数に比べて説明変数の数が極端に多い場合でも問題なく分析が可能です。 

3. 「複数の目的変数」を一度に分析できる

通常の重回帰分析は、一度に扱える目的変数は1つだけです。一方、PLS回帰は目的変数の数に応じて、以下2つのアルゴリズムで柔軟に計算を行えます。

PLS1 回帰（目的変数が1つの場合）: 
通常の回帰分析と同様に、1つの目的変数を予測するためのモデルを作成します。

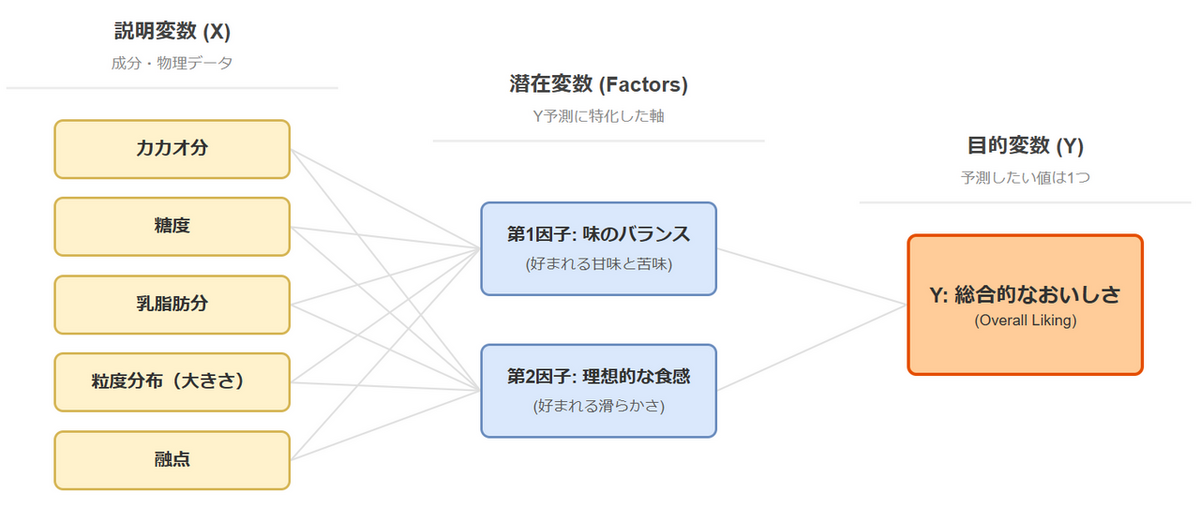
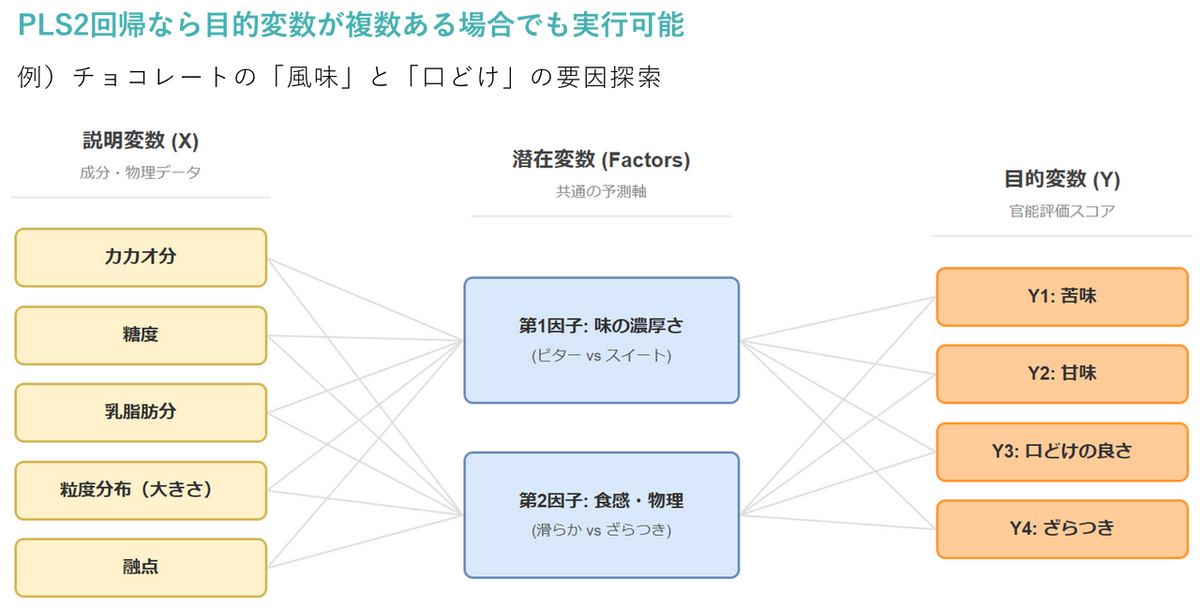
PLS2 回帰（目的変数が複数の場合）：
複数の目的変数を同時に説明できる「共通の成分」を抽出します。個別の目的変数ごとのモデルを作るのではなく、「目的変数全体の相関構造」を捉えることができるのが特徴です。

なお、XLSTAT では、選択したデータの列数に応じて自動的にPLS1/PLS2 が切り替わるため、ユーザーが意識して設定する必要はありません。

4. 判別分析もできる

後述するように、従属変数の尺度によって、回帰分析もしくは判別分析が選択できます。

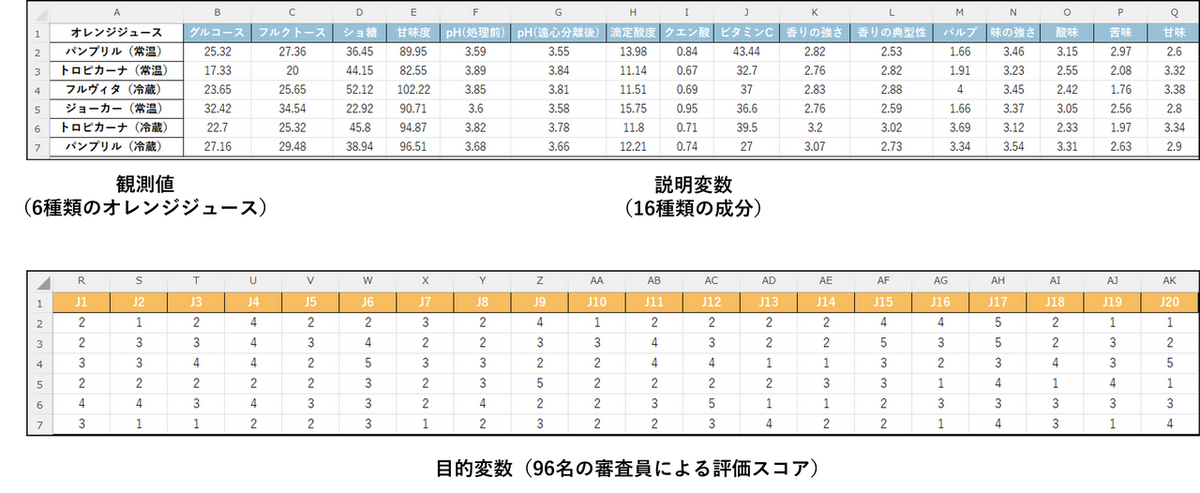
PLS回帰を実行するためのデータセット

このページでは、Tenenhaus et al. (2005) の研究で使用された「オレンジジュースのデータセット」を使用します。このデータではサンプル数が6つに対し、説明変数が16個あり、通常の重回帰分析では実行できませんが、PLS回帰なら分析が可能です。

• データ形式： 
  行にオレンジジュース（サンプル）、列に変数を配置したテーブル形式
  
  
• Ａ列：オレンジジュース
  6種類のオレンジジュース名（パンプリル、トロピカーナ等の常温・冷蔵製品）
  
  
• Ｂ列～Ｑ列：
  16種類の物理・化学的特性値（グルコース、pH、酸味、ビタミンC など）。今回はこのデータを「X /説明変数」として設定する。
  
  
• R列～DI列：
  96人の審査員によるおいしさの評価スコア（5段階）。この96列をまとめて「Ｙ/従属変数（目的変数）」として設定します。

今回はこのデータに対してPLS回帰を実行し、オレンジジュースの成分から、96人の審査員によるおいしさの評価を予測・分析します。

サンプルデータのダウンロードはこちらから

sample-data-for-PLS-regression.xlsm

PLS回帰を実行する手順

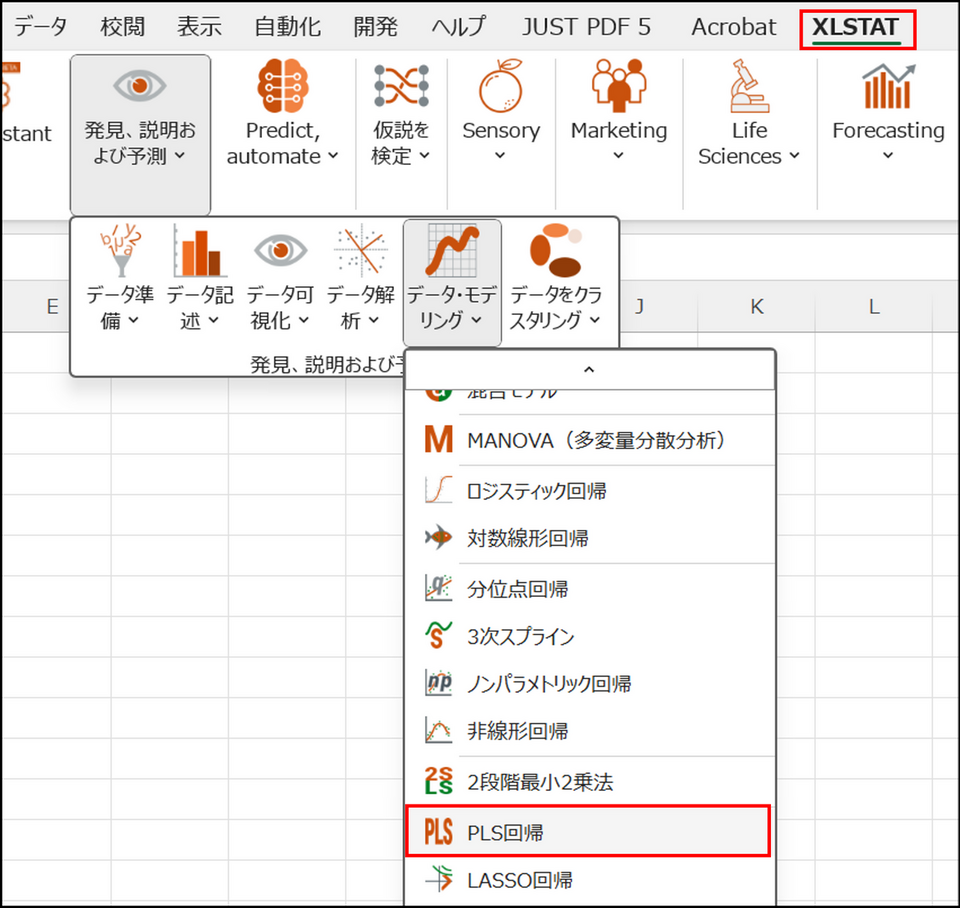
1. XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [PLS回帰] を選択します。

   

2. ダイアログボックスが表示されたら、以下のようにデータを選択します。

   

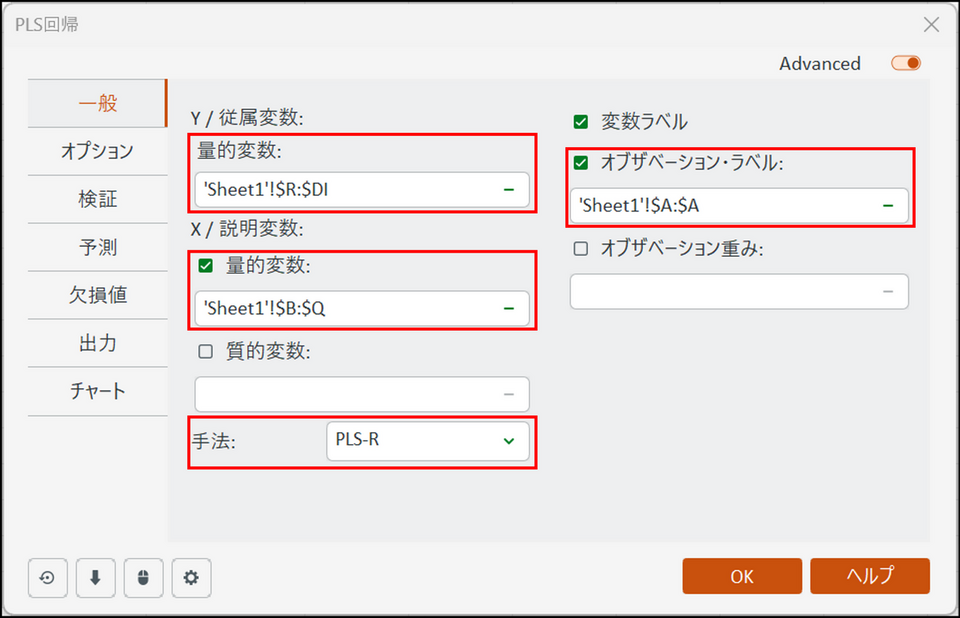
   • Y / 従属変数：96人の審査員の評価データ（R 列〜CS 列）を選択します。
   • X / 説明変数：量的変数にチェックを入れ、16種類の物理・化学的な測定項目（B 列〜Q 列）を選択します。
   • オブザベーション・ラベル：A 列にあるオレンジジュースの銘柄を選択します。
   • 手法：デフォルトの「PLS-R」を選択します。（通常、Y / 従属変数の嗜好点は連続尺度と考え、Regression（回帰）を選択します。従属変数が名義尺度の場合は（PLS-DA　Discriminate　Analysis）を選択し判別分析を実行します。）

3. [オプション] タブに切り替え、モデルの作り方と検証方法を指定します。

   

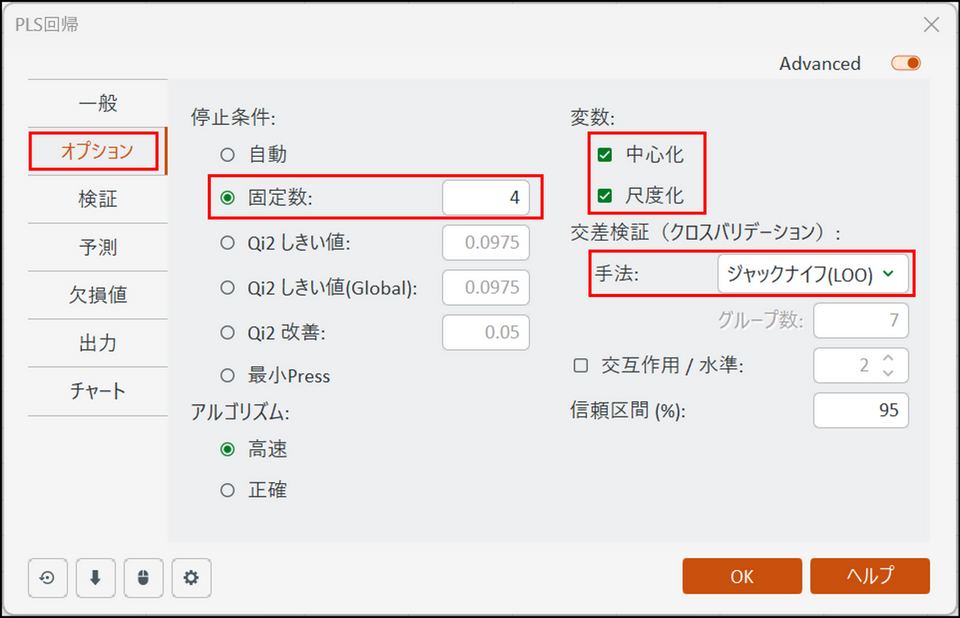
   • 停止条件：[固定数] を選択し、「4」と入力します。
     「停止条件」とは、PLS回帰モデルを作成する際に、「成分（Comp）をいくつまで抽出して計算を終了するか」を決めるためのルールのことです。PLS回帰は、元のデータを「第1成分」「第2成分」「第3成分」…と、重要度の高い順に成分を作成していきます。しかし、成分を増やしすぎると、データのノイズ（意味のない細かい変動）まで取り込んでしまい、モデルの精度が落ちてしまいます。そこで、どこかのタイミングで計算を止める必要があり、そのルールを決めるのがこの項目です。今回は、オレンジジュースの味のデータを4つの成分に要約するように設定しておきます。

   ---

   • 交差検証（クロスバリデーション）：[ジャックナイフ(LOO)] を選択します。
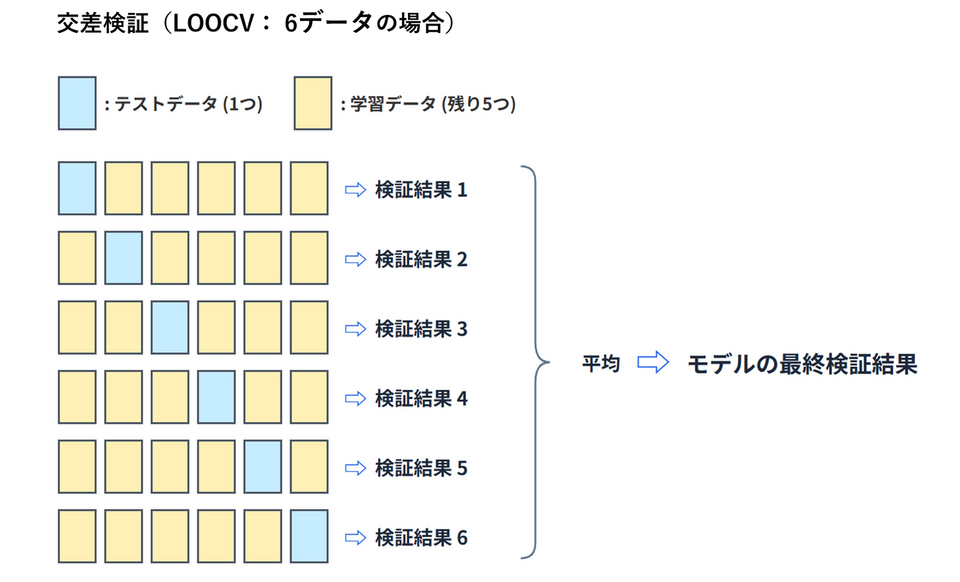
     「交差検証」とは作成したモデルが「たまたま手元のデータに合っているだけ」なのか、「新しいデータでも通用する」のかをチェックするテストのことです。 具体的には手持ちのデータを「学習用（モデルを作るためのデータ）」と「テスト用（モデルの正解率を確かめるためのデータ）」に何度も分け直して検証を繰り返します。通常、データを一度だけ分割して評価を行うと、たまたま「簡単なデータ」がテスト用に選ばれたり、逆に「難しいデータ」ばかりが集まったりして、モデルの本当の実力を見誤るリスクがあります。そこで交差検証では、データを複数のグループに分割し、「テスト役」を順番に交代させながら全てのグループでテストを行います。最終的にそれら全てのテスト結果を平均することで、データの偏りによる偶然性を排除し、モデルが未知のデータに対してどれくらい通用するかを正確に見極めることができます。「ジャックナイフ (LOO)」は、「1つ抜き交差検証（Leave-One-Out Cross-Validation: LOOCV）」とも呼ばれ、データ数が極端に少ない場合に有効な手法です。この手法では「手持ちのデータから1つだけをテスト用に抜き出し、残りの全てを学習用に使う」という手順を、すべてのデータが一度ずつテスト用になるまで繰り返します。今回のデータセットには6種類のジュース（6行のデータ）があるため、「5種類のジュースで学習して、残りの1種でテストする」という作業を、対象を変えながら6回行います。

   

   ---

   • [変数]：[中心化] と [尺度化] にチェックを入れます。
     
     
   • [交互作用]：説明変数間の交互作用も考慮に入れたいときは選択します。（通常2次）ただし、計算時間は増えます。

4. [出力] タブに切り替え、以下のように設定します。

   

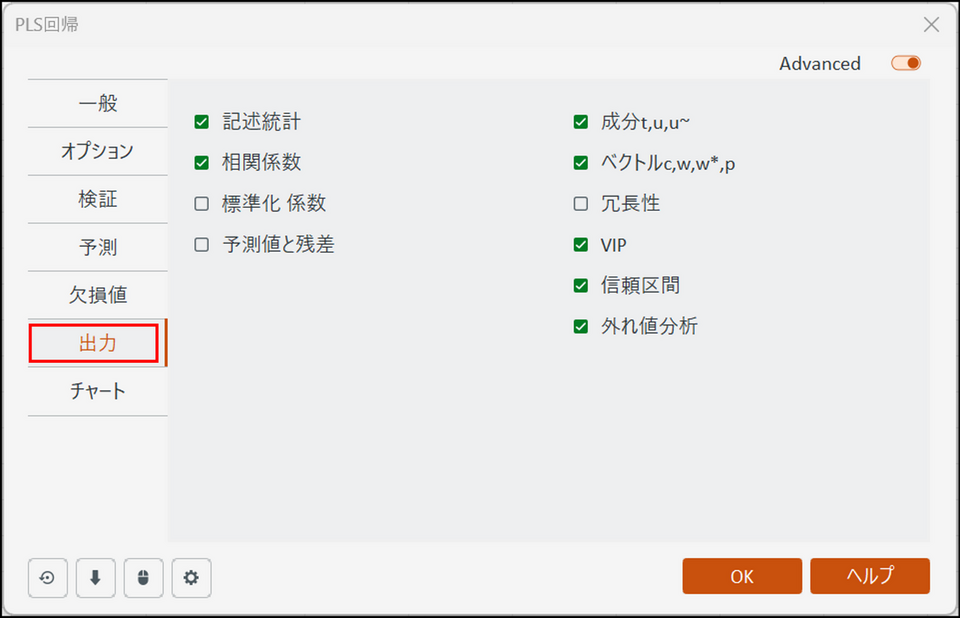
   今回のように目的変数が非常に多い場合、デフォルト設定のまま実行すると膨大なレポートとグラフが出力され、処理が重くなるため、全体の傾向を効率よく把握したい場合には、[予測値と残差] と[標準化 係数] 項目のチェックは外しておくことをおすすめします。

5. [チャート] タブに切り替え、以下のように設定します。

   

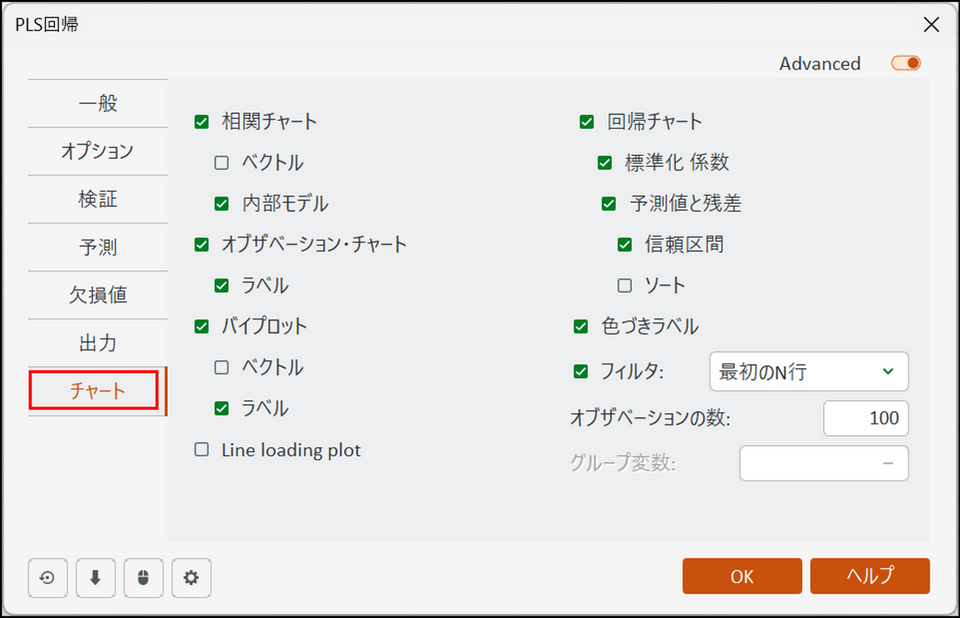
6. [OK] をクリックすると計算が始まり、結果が別シート（PLS-R）に出力されます。「軸の選択」画面が表示された場合は、デフォルトのまま [完了] をクリックしてください。

   

出力結果の解釈

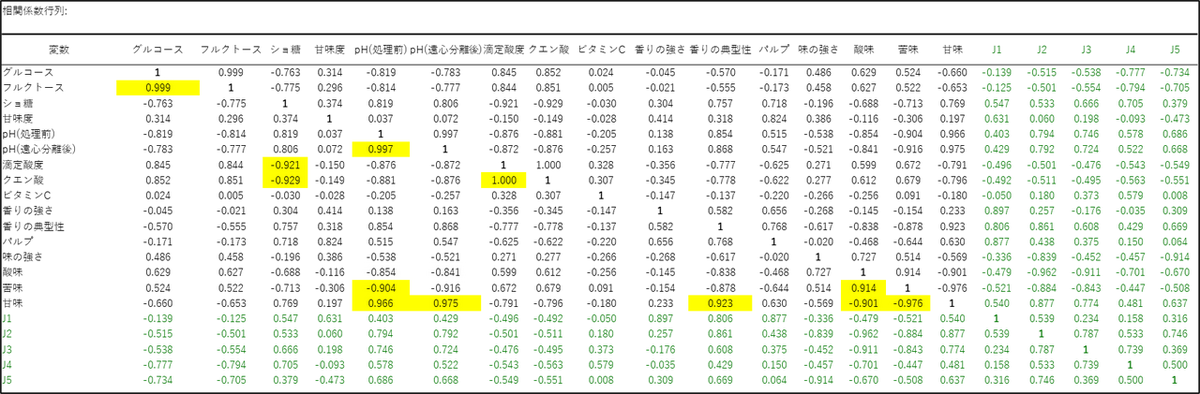
相関係数行列

元の変数同士の関係性を確認する表です（-1.0〜1.0 で表示）。目的変数（従属変数）は緑色、定量的予測変数は黒色で表示されます。下記画像は一部抜粋し、説明変数同士の相関係数の絶対値が0.9 を超えるセルをハイライトしています。

この表からは、データ内に強い関係性（相関）を持つ変数が多数含まれていることが読み取れます。まず、多重共線性（強い相関） が疑われる組み合わせがいくつか確認できます。「グルコース」と「フルクトース」の相関が 0.999 と非常に高いほか、「pH」と「酸味」、「ショ糖」と「滴定酸度」など、オレンジジュースの物理・化学的特性の間にも強い相関が見られます。これらは通常の回帰分析ではエラーの元となりますが、PLS回帰ではこれらをまとめて「成分」として扱えるため、分析の強みが活きるデータと言えます。また、「甘味」と「苦味」の相関は -0.976 であり、強いトレードオフの関係（甘いジュースは苦くない）が見て取れます。一方で「ビタミンC」は他のどの変数とも相関が低く、独自の動きをしていることがわかります。

モデル品質

作成されたモデルの「成績表」です。表内の「Comp」とは Component（成分） の略で、バラバラだった元の変数を要約した「新しい合成変数」のことです。統計学的には「潜在変数」とも呼ばれますが、このページでは同じ意味として扱います。

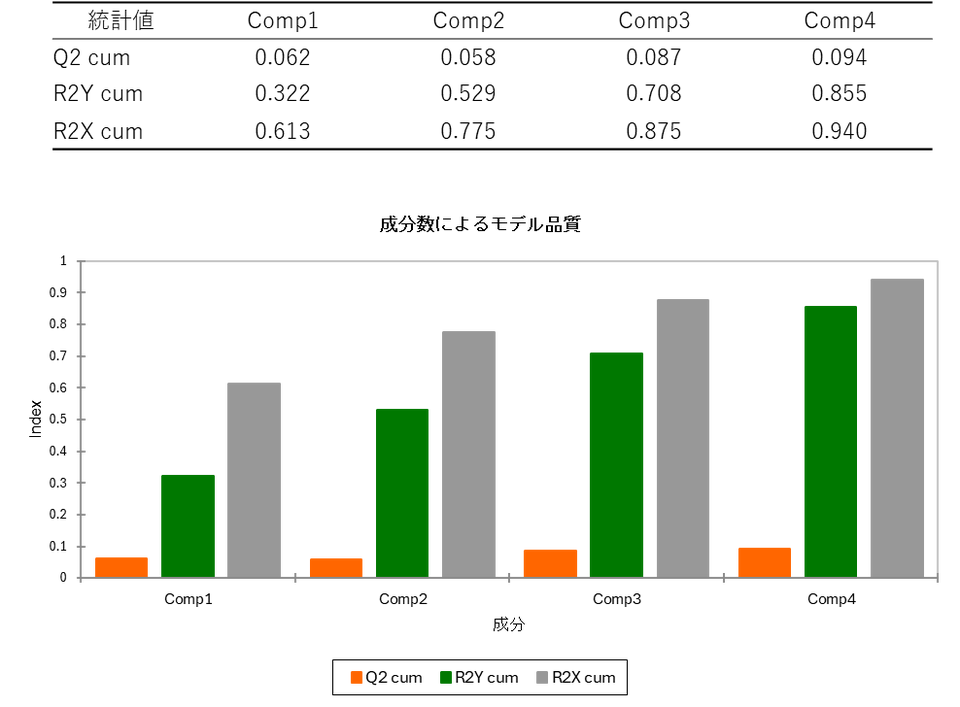
表では成分（Comp）を1つ、2つと増やしていったときに、モデルの性能がどのように変化するかを示しています。各指標の意味は以下の通りです。

Q2 cum（累積Q2）：

この指標は、最初の数個の成分が、モデル全体の「予測品質」にどれだけ寄与しているかを測るものです。指標の計算には、PRESS 統計量（算出には交差検証が必要）と、成分が1つ少ないモデルにおける誤差平方和（SSE）が用いられます。このQ2 指標が最大となるポイントを探すことは、「最も安定したモデル」を見つけることと等しい意味を持ちます。

R2Y cum（累積R2Y）：

この指標は、「目的変数（従属変数）」と抽出された成分との間の決定係数の合計です。したがって、これは抽出された成分（comp）が、モデルの「目的変数（従属変数）」をどれだけ説明できているかという説明力の尺度となります。

R2X cum（累積R2X）：

この指標は、「説明変数」と抽出された成分との間の決定係数の合計です。したがって、これは抽出された成分（comp）が、モデルの「説明変数」をどれだけ説明できているかという説明力の尺度となります。

R2X cum とR2Y cum を見ると、Comp4（4成分）の時点で1に近く、非常に高い数値を示しています。これはPLS回帰モデルが説明変数と目的変数（従属変数）の両方を効果的に要約していることを意味しています。一方で、予測力（Q2 cum）はComp4 でも 0.094 と低く留まっています。このことから今回作成されたモデルは、「過去のデータの説明（分析）には使えるが、未来の予測には向かない」という解釈になります。

成分tとu~による変数の相関係数行列

この表は各成分（t1〜t4）と元の変数との相関係数を示しています。なお、XLSTAT の表示上、使われる場所によって名前が使い分けられていますが、t と Comp どちらも「成分（潜在変数）」のことを指しています。

まず第1成分（t1）の列に注目すると、「pH」や「甘味」が高い正の相関を示す一方で、「酸味」や「苦味」は高い負の相関を示しています。このことから、第1成分はジュースの「甘さと酸っぱさのバランス」という、最も主要な味の軸を表していることが分かります。次に第2成分（t2）の列を見ると、「甘味度」や「パルプ（=果肉量・繊維量）」が高い正の相関を示しています。これは、単純な味のバランスとは異なる、ジュースの「濃厚さ」や「ボディ感」を表す軸であると解釈できます。興味深いのが第3成分（t3）です。ここでは「ビタミンC」だけが突出して高い相関を示し、他の変数はほとんど関係していません。つまり、ビタミンC は味の主軸（t1, t2）とは独立して変動する、独自の要素であることが読み取れます。

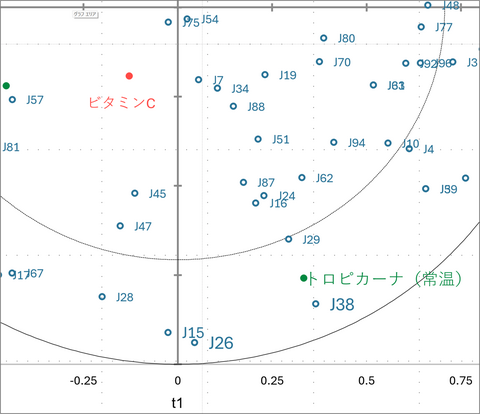
相関マップ

相関マップは、第1成分（t1：横軸）と第2成分（t2：縦軸）によって張られる空間上での、説明変数（オレンジジュースの物理・化学的特性）（X）と審査員（Y）の関係を可視化しています。

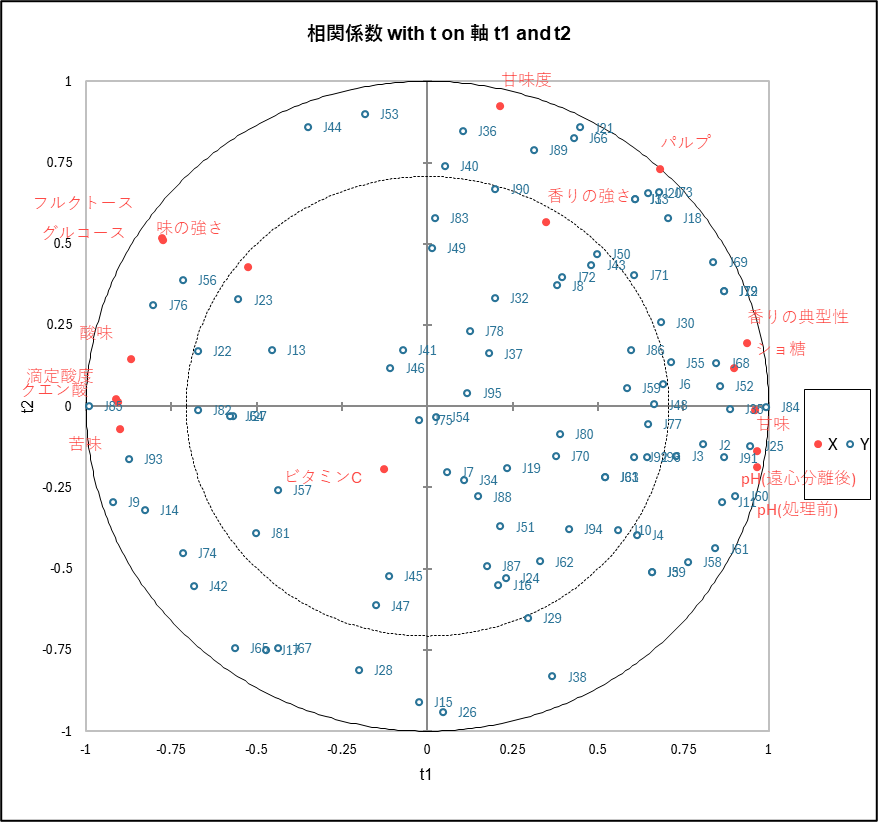
まず、測定データ（赤い点）の位置関係を見ると、右側には「甘味」「pH」が、左側には「酸味」「滴定酸度」が集まっています。これにより、横軸（t1）は「成分tとu~による変数の相関係数行列」での解釈通り「甘味 vs 酸味」のバランスを表していることが視覚的にも確認できます。

次に審査員（青い点）を見ると、右側にいる審査員は「甘味」の近くにいるため甘党、左側にいる審査員は「酸味」の近くにいるため酸味を好む傾向があることがわかります。また、青い点が特定の場所に固まらず円全体に散らばっていることは、好みが多様であることを視覚的に証明しており、先ほどのQ2 cum（予測品質）が低かった理由を裏付けています。

w ベクトル, w* ベクトル, c ベクトル

これらのベクトル表は「説明変数（X）と目的変数（Y）の関係性、および各変数がモデル（成分）にどのように寄与しているか」を示したものです。

w ベクトル と w* ベクトル

この表は、分析によって抽出された「成分（第1成分、第2成分…）」が、具体的にどのような特徴を表しているかを数値で示しています。絶対値が大きいほど、その成分に対する寄与度が大きいことを意味します。なお、w ベクトルは、個々のPLS 成分を計算するための直接的な寄与度であるのに対し、w* ベクトルは変数の相関関係を考慮して変換された最終的な寄与度です。解釈には通常、後者のw* ベクトルが使われます。後述するマップでも、この値が座標として使用されます。

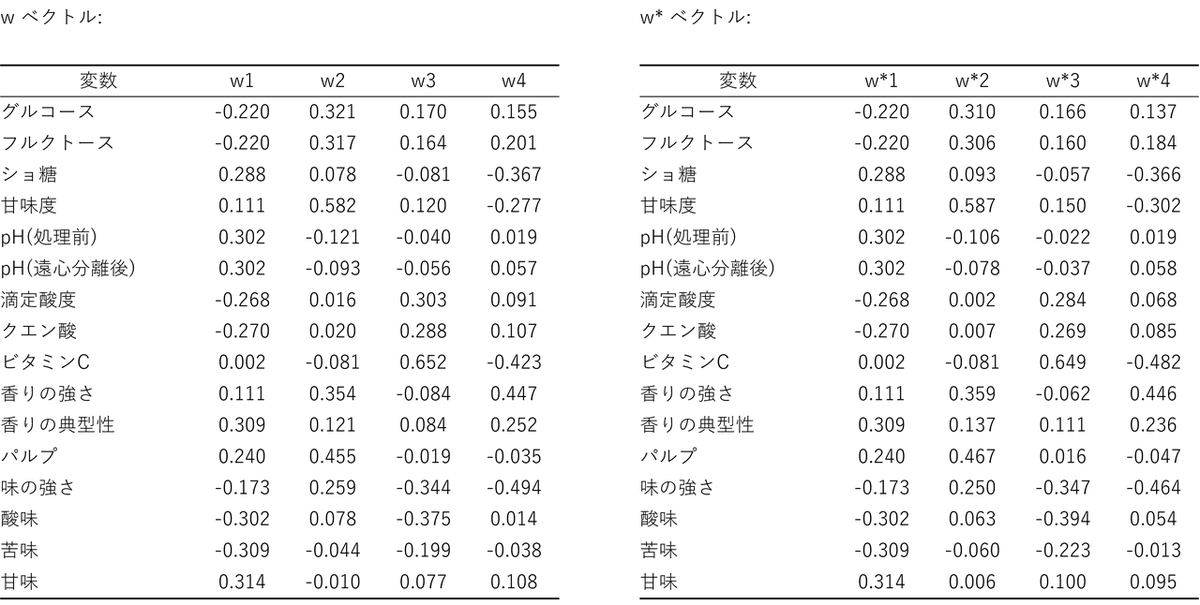
各列の数値は「二乗してすべて足し合わせると合計が 1 になる」ように調整されています。今回のデータには変数が16個あるため、もし全ての変数が平等に影響し合っているならば、その数値は「1 ÷ 16 の平方根」、つまり 「0.25」 になります。したがって、この 0.25 という平均ラインを明確に超えている 「0.3 前後（またはそれ以上）」の数値を持つ変数は、その成分の特徴を決定づける変数であると判断できます。この基準を踏まえて、主要な第1成分と第2成分を見ていきましょう。

• 第1成分（w*1）：
  最も主要な軸であるこの成分の数値を見ると、負の方向には「苦味（-0.309）」「酸味（-0.302）」「クエン酸（-0.270）」といった刺激に関する変数が基準値（0.25）を超える高い寄与度で並んでいます。対照的に、正の方向には「甘味（0.314）」「pH（0.302）」「ショ糖（0.288）」が 0.3 前後の高い数値で拮抗しています。つまり、第1成分のスコアが低いほど酸味や苦味が強く、高いほど甘くマイルドであるという、味の好みを分ける最も大きな要因がここに表れています。このことから第1成分は、製品の味の基本骨格である 「酸味・刺激」対「甘味・マイルドさ」のバランス を表していると解釈できます。
  

• 第2成分（w*2）：
  ここで基準値を大きく超えて突出しているのは、「甘味度（0.587）」「パルプ（0.467）」「香りの強さ（0.359）」です。特に甘味度の寄与度は0.6 に迫る勢いで、この成分の核心と言えます。また、第1成分では負の方向に寄与していた「グルコース」などが、ここではプラス側で「甘味度」「パルプ」「香りの強さ」と同じ方向に現れている点も特徴的です。これらの変数がまとまって高い寄与度を示していることから、第2成分は、味の種類そのものではなく、ジュースの「濃厚さ・ボディ感」を表す軸と解釈できます。

c ベクトル

この数値は、抽出された成分と、各審査員の評価がどれくらい連動しているかを示しています。読み方の基本ルールは w* と同じで、数値の「プラス・マイナス」が好みの方向を、「絶対値の大きさ」がそのこだわりの強さを表します。

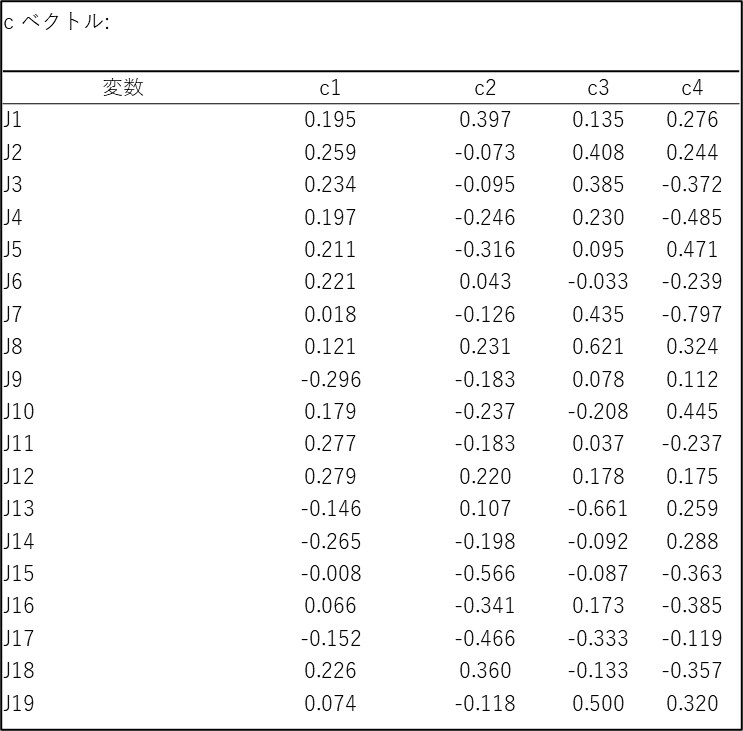
上記W* ベクトルの解釈で、第1成分（横軸）は「酸味・刺激（マイナス）」対「甘味・マイルド（プラス）」、第2成分（縦軸）は「濃厚・ボディ感」を表す軸であると定義されました。この定義を、今回の c ベクトル表に当てはめると、審査員を以下のような「嗜好グループ」に分類することができます。

まず 第1成分（c1） の列に注目すると、審査員が「酸味派」か「甘味派」かが分かります。例えば、J9（-0.296） や J85（-0.318）、J93（-0.280） といった評価者は、負の方向に大きな数値を持っています。第1成分のマイナス側は「酸味・苦味」なので、この審査員は「酸味や刺激のある味を好む（酸味が高いと評価が上がる）グループ」であると言えます。

一方で、J25（0.303） や J60（0.289）、J84（0.318） はプラスの高い数値を示しています。第1成分のプラス側は「甘味・pH」でしたので、彼らは「マイルドで甘い味を好むグループ」です。このように、c1 の符号を見るだけで、その人が酸味を求めているか、甘味を求めているかが判別できます。

次に 第2成分（c2） の列を見ると、ジュースの「飲みごたえ」に対する好みが分かります。ここで顕著なのが、J21（0.533）、J36（0.527）、J53（0.559）、J66（0.513） といった審査員たちです。彼らは0.5 を超える非常に高いプラスの数値を示しています。第2成分のプラス側は「パルプ・甘味度・香り」という「濃厚さ」を表すものでした。つまり、彼らは「果肉感があり、濃厚で香りが強いリッチなタイプのオレンジジュースを好むグループ」と解釈できます。

逆に、J15（-0.566） や J26（-0.584） 、J38（-0.52）のように強いマイナスを示す人たちは、濃厚さが評価にマイナスに働く、つまり「サラッとした飲み口や、すっきりしたタイプを好むグループ」であると推測できます。

ベクトル表の後には「w* ベクトル表」と「c ベクトル表」の数値を、そのまま座標としてプロットしたマップが表示されます。

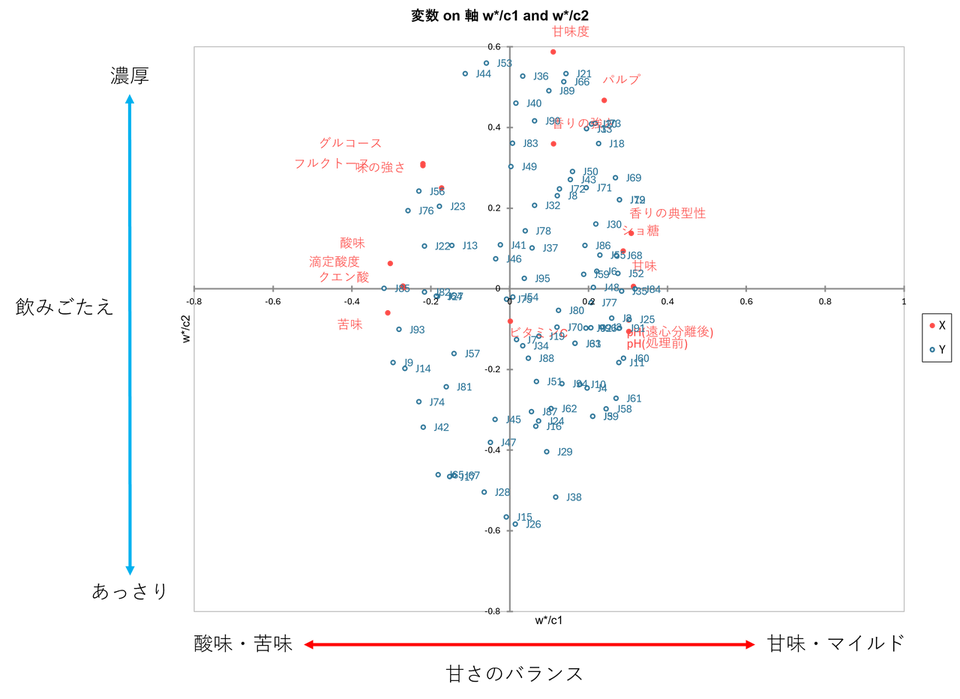
※結果を解釈しやすくするため、画像には軸の説明（「酸味・苦味⇔甘味・マイルド」「濃厚⇔あっさり」）を加えています。

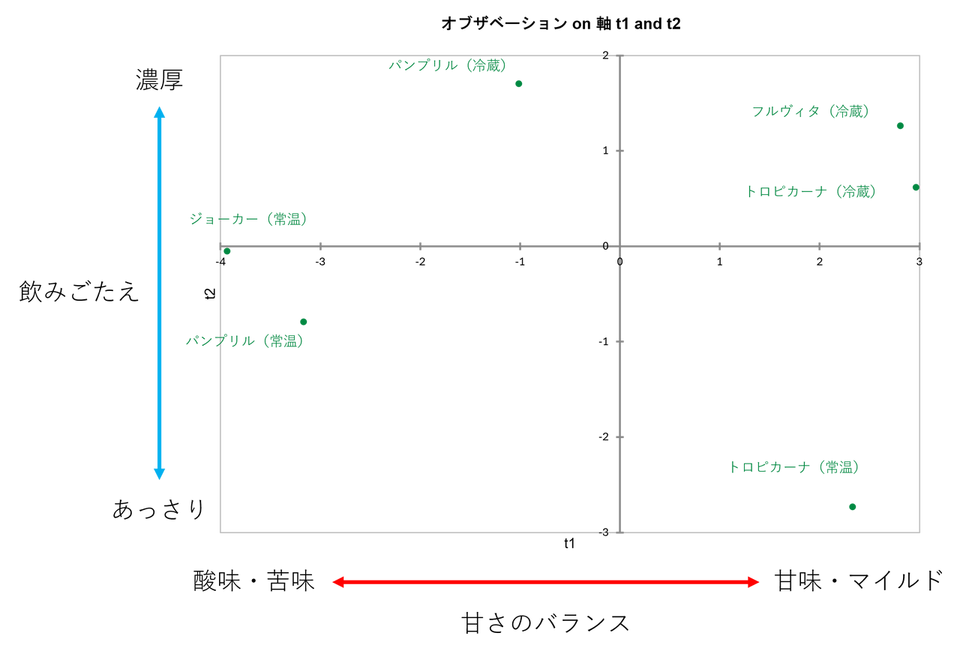
得点 on t

この表は、分析対象となった6種類のジュースが、抽出された成分軸の上でどのような位置付けにあるか、つまり「それぞれの製品がどのような個性を持っているか」を数値で示したものです。

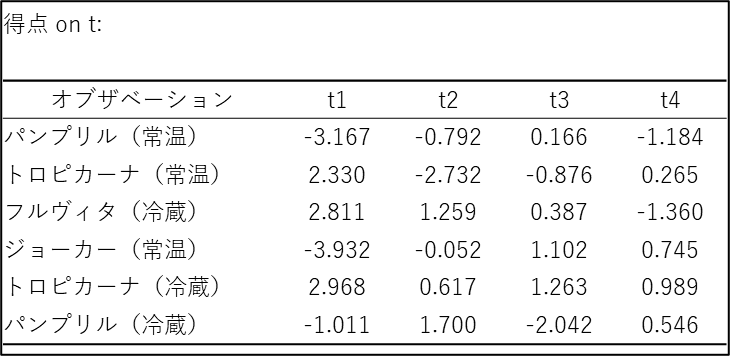
これまでの分析で、第1成分（t1）は「酸味・刺激」対「甘味・マイルド」、第2成分（t2）は「濃厚・ボディ感」対「あっさり」を表す軸であると定義されました。この定義という「ものさし」を使って、各製品の数値を読み解くと、それぞれの味のプロフィールが明確に浮かび上がります。

まず、第1成分（t1：甘味バランス） の列を見ると、製品ごとの味の骨格がはっきりと分かれています。 ここで際立って低い数値（マイナス）を示しているのが 「ジョーカー（常温）」の -3.932 と 「パンプリル（常温）」の -3.167 です。これらは酸味や苦味といった刺激的な特徴を持っており、大人向けの製品であると推測できます。 対照的に、高い数値（プラス）を示しているのが 「トロピカーナ（冷蔵）」の 2.968 や 「フルヴィタ（冷蔵）」の 2.811 です。これらは酸味が抑えられ、甘くマイルドで飲みやすい設計のジュースであることが分かります。

次に、第2成分（t2：飲みごたえ） の列を見ると、口当たりの違いが見えてきます。 プラスの方向に高い数値を示しているのは 「パンプリル（冷蔵）」の 1.700 や 「フルヴィタ（冷蔵）」の 1.259 です。これらは果肉感（パルプ）やとろみのある、濃厚でリッチなボディ感を持っています。 一方で、極端なマイナス値を示しているのが 「トロピカーナ（常温）」の -2.732 です。これは非常にあっさりとしていて、サラッとした飲み口のライトなタイプであることを意味します。

興味深いのは、同じブランド内での比較です。例えば「パンプリル」を見ると、常温版は「酸味が非常に強い（t1: -3.1）」のに対し、冷蔵版は「酸味は控えめ（t1: -1.0）で、濃厚さ（t2: 1.7）がある」というように、温度帯や商品ラインによって全く異なる味作りがなされていることが、この数値から読み取れます。同様に「トロピカーナ」も、常温版は「あっさり（t2: -2.7）」ですが、冷蔵版は「標準的な濃度（t2: 0.6）」と、明確な差別化が図られています。

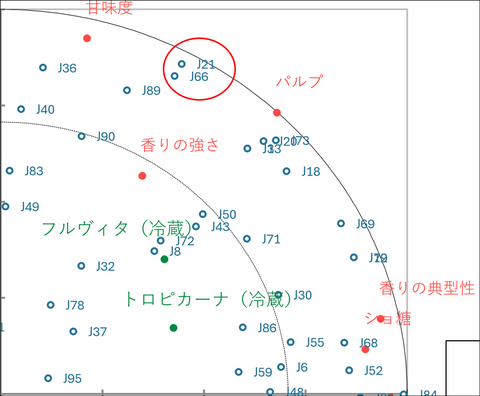
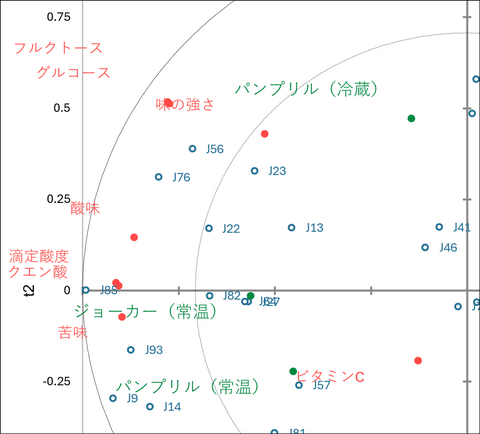
表のあとには「得点 on t」の数値をそのまま座標としてプロットしたマップが表示され、競合製品との位置関係や、表で確認したブランドごとの味の特徴を視覚的に把握することができます。

バイプロット

ここまでに登場した「成分」「説明変数（赤）」「目的変数（青）」「製品（緑）」のすべての関係性を一枚のマップで可視化しています。

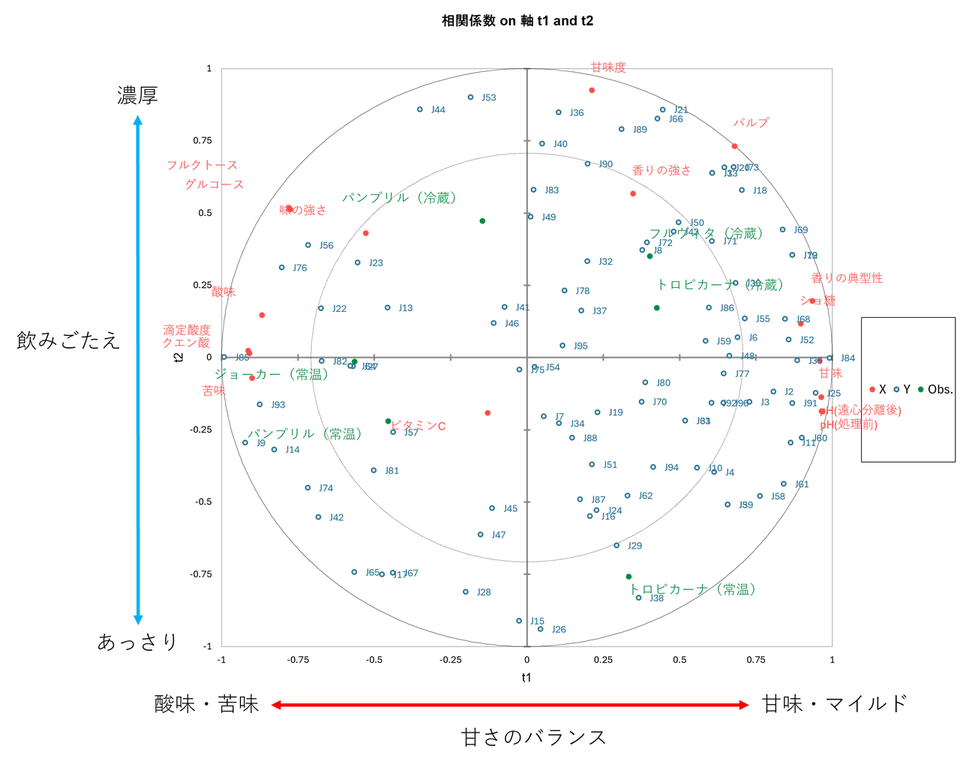
マップの右上には、赤点の「パルプ」「甘味度」があり、すぐ近くに緑点の「フルヴィタ（冷蔵）」「トロピカーナ（冷蔵）」が位置しています。さらに、その周囲をJ21やJ66などの青点（評価者）が取り囲んでいます。これは、「フルヴィタやトロピカーナ（冷蔵）はパルプや甘味度が強く、その特徴を好む評価者たちがこのエリアに集結している」ということを示しています。

対照的に、マップの左側には赤点の「酸味」「苦味」があり、同じ方向に緑点の「ジョーカー（常温）」や「パンプリル（常温）」が位置しています。ここにもJ9やJ93などの青点が重なっており、「酸味の強いこれらの製品は、酸味を好む特定の評価者層に支えられている」ことが分かります。

そして、マップの下側には緑点の「トロピカーナ（常温）」が位置しています。興味深いことに、この方向には強い意味を持つ赤点（肯定的な成分）があまり見当たりません。強いて言えば第2成分（濃厚さ）のマイナス方向なので、「濃厚さがない（あっさりしている）」という特徴とリンクしており、その周囲に位置する評価者（J38、J26など）は、特定の成分の強さではなく、この「軽さ」を支持している層であると解釈できます。

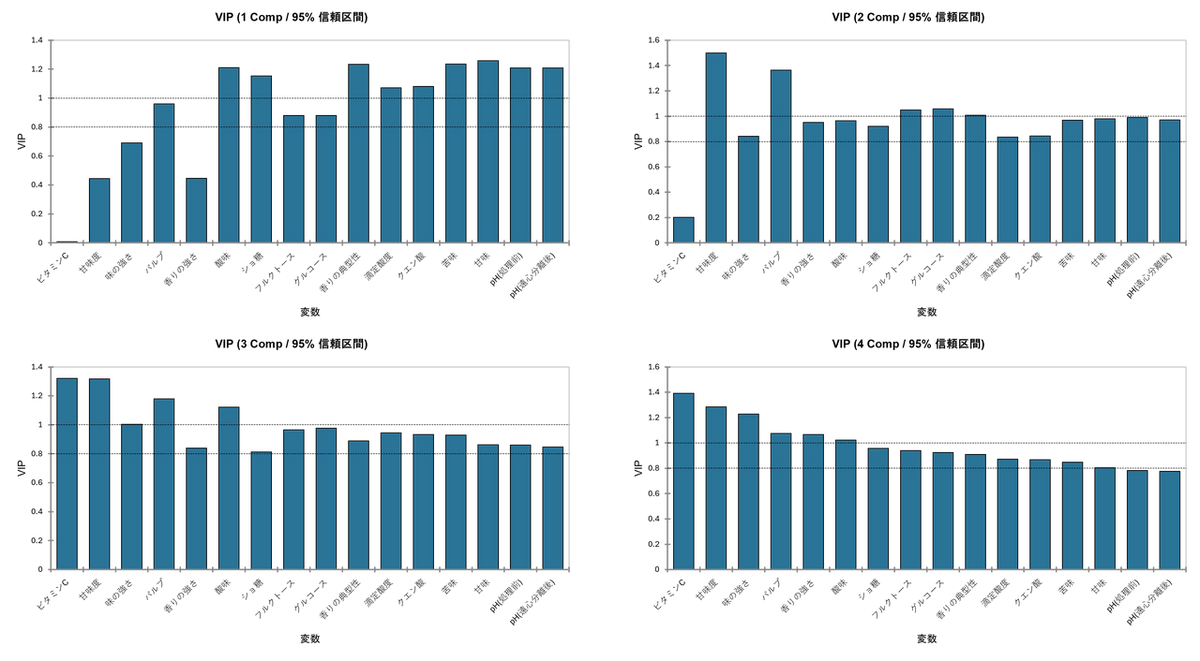
VIPチャート

VIP（Variable Importance in the Projection）とは、これまで見てきた「重み（w*）」や「成分」といった細かな情報をすべて統合し、最終的に「どの変数が製品の違いを説明するのに最も役に立ったか」を単一のスコアでランク付けしたものです。

このグラフを見る上で、最も重要な判断基準となる「ボーダーライン」があります。グラフにも点線で引かれていますが、一般的にVIP の値が 「1.0」を超えている変数は「非常に重要」、「0.8」を下回る変数は「影響力が低い（重要でない）」と判断されます。

この基準に従ってデータの推移を見ていくと、分析モデルがどのように変数の重要性を認識していったかが分かります。まず、最も基本的なモデルである「VIP(1 Comp)」のグラフを見ると、「甘味」「苦味」「酸味」「pH」 といった味の基本骨格に関わる変数が軒並み「1.0」を超えています。これは、第1成分（酸味vs甘味）がジュースの個性を決める最大の要因であったことと完全に一致しており、これらの変数がまず最初に「最重要」として認識されたことを示しています。

次に、成分を2つに増やした「VIP(2 Comp)」を見ると、評価が一変する変数があります。特に注目すべきは 「甘味度」 と 「パルプ」 です。これらはVIP(1) の段階では重要視されていませんでしたが、VIP(2) になった途端にスコアが急上昇し、「1.0」を大きく超えてきました。これは、第2成分（濃厚さ・ボディ感）という視点が加わったことで、「この変数は濃厚さを語る上で外せない重要な要素だ」と再評価されたことを意味します。

さらに興味深いのが 「ビタミンC」 の動きです。VIP(1) やVIP(2) の段階ではスコアはほぼゼロに近く、重要ではないと見なされていました。しかし、「VIP(3 Comp)」以降の表を見ると、スコアがいきなり 1.3 以上へと跳ね上がっています。これは先ほどの分析で「第3成分はビタミンC 特化の軸である」と確認した通り、成分を3つまで増やして初めて、ビタミンC という隠れた個性が重要性を持って浮かび上がってきたことを証明しています。

最終的な「VIP(4 Comp)」の表は、これら全ての成分を考慮した「最終成績表」です。ここでは、ビタミンC、甘味度、パルプ、そして酸味や苦味といった多くの変数が「1.0」を超えており、これら全ての要素が複雑に絡み合ってジュースの個性を形成していることが分かります。逆に、これだけ成分を重ねても「0.8」前後に留まっている変数（例えば「滴定酸度」や「クエン酸」など）は、他の変数（酸味など）で代用が可能であり、あえて単独で注目する必要性はないと結論づけることができます。

モデル・パラメータ

この表は、個々の説明変数がそれぞれどの程度、結果（各審査員の評価）に影響を与えているのかを示しています。

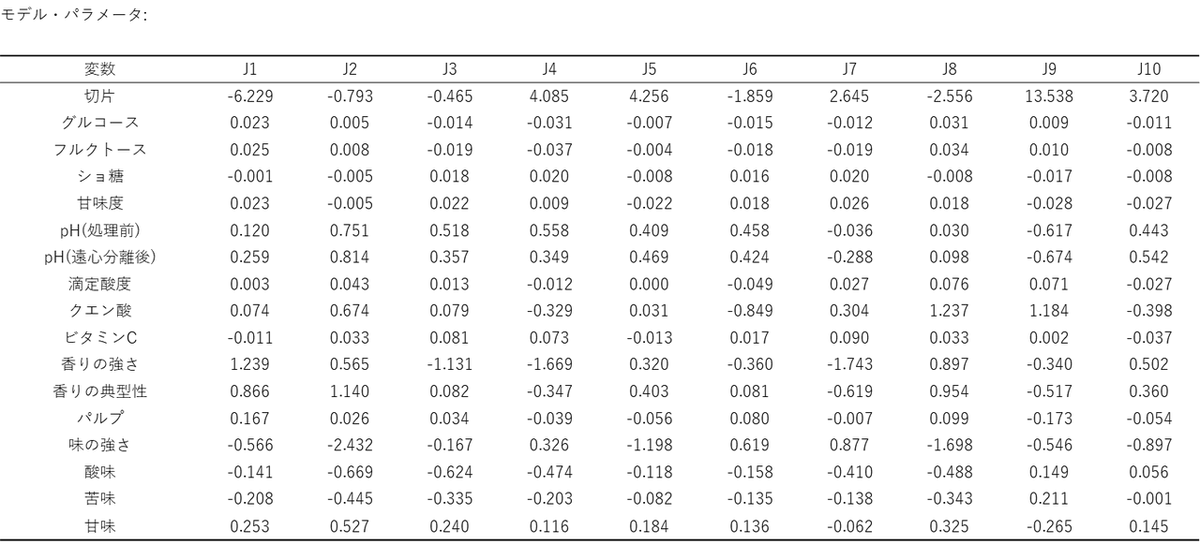
表の見方

• 数値の符号（＋/－）： 
  プラスなら「増やすと評価が上がる」、マイナスなら「増やすと評価が下がる」ことを意味します。
  
  
• 数値の大きさ：
  影響の度合いです。数値が大きいほど、少しの変更で評価が大きく変動します。

「酸味好き」であることが分かっている評価者 J9 の列を見ると、クエン酸が「1.184」、pH（処理前）が「-0.617」 となっています。これは、クエン酸を添加し、pH を下げる（酸性を強める）ことが評価向上に直結することを示しています。例えば、クエン酸の数値を 0.5 単位増やした場合、J9 の評価は「1.184×0.5 =約0.6ポイント」上昇すると予測できます。

分析結果のまとめ

今回の分析結果を総括すると、以下の結論が導き出されます。

まず、モデルの予測精度（Q2）が決して高くはないことや、相関マップ上で審査員の評価位置が特定の場所に集中せず全体に分散している事実から、消費者の好みは極めて多様であることが統計的に示されました。これは、万人に共通する単一の「正解の味」は存在せず、一つの製品ですべての消費者を満足させることは困難であることを意味しています。

その一方で、おいしさを左右する要素については明確な手がかりが得られました。VIP チャートの分析により、「ビタミンC」「甘味度」「味の強さ」の3項目は、多くの審査員の評価に強く影響を与える共通の重要因子であることが特定されました。対照的に、「pH」の数値そのものはおいしさに対する直接的な影響力が低いことも判明しています。

これらの知見を踏まえると、今後の製品開発においては、全員に向けた平均的な製品を目指すのではなく、相関マップで可視化された好みの傾向に基づき、「甘味を重視する層」や「酸味を重視する層」といったターゲットごとのセグメンテーションを行うことが推奨されます。それぞれの好みに特化した製品開発を行うことこそが、結果として市場全体の満足度を高めるための有効な戦略であると言えます。

なお、チュートリアルデータでは、各評価者毎に回帰を行っていますが、実際は、全パネルやパネルクラスターの嗜好点の平均を回帰することも多く行われます。

まとめ

PLS回帰は、一般的な回帰分析では扱いが難しい「多重共線性（変数間の強い相関）」の問題に対処でき、サンプル数が変数の数より少ない場合でも安定したモデルを構築できる点が特徴です。そのため、限られた製品数に対して多数の成分データや評価項目が存在する今回のような官能評価の現場において、非常に有効な手法となります。XLSTAT を活用すれば、こうした高度な多変量解析を使い慣れたExcel 上で直感的に実行することが可能です。複雑な計算結果も、成分の意味を紐解くベクトル表や、製品のポジショニングを示すマップとして視覚的に出力されるため、統計の専門知識がなくとも「どの成分が重要か」「誰をターゲットにすべきか」といった具体的な戦略をスムーズに読み取ることができます。データに基づいた確かな意思決定を支援するツールとして、ぜひXLSTAT をご活用ください。

記事監修：小田井　英陽
（一般社団法人日本官能評価学会理事、東京バイオテクノロジー専門学校講師）

参考文献

• XLSTAT: Partial Least Squares PLS regression tutorial in Excel
  https://community.lumivero.com/s/article/6636-partial-least-squares-pls-regression-excel?langua
  ge=en_US

• Tenenhaus M, Pagès J, Ambroisine L, Guinot C. PLS methodology to study relationships between hedonic judgements and product characteristics. Food Qual Prefer 2005; 16: 315–25, https://doi.org/10.1016/j.foodqual.2004.05.013.

XLSTAT の無料トライアル

トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介したPLS回帰はStandard と Advanced のライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。