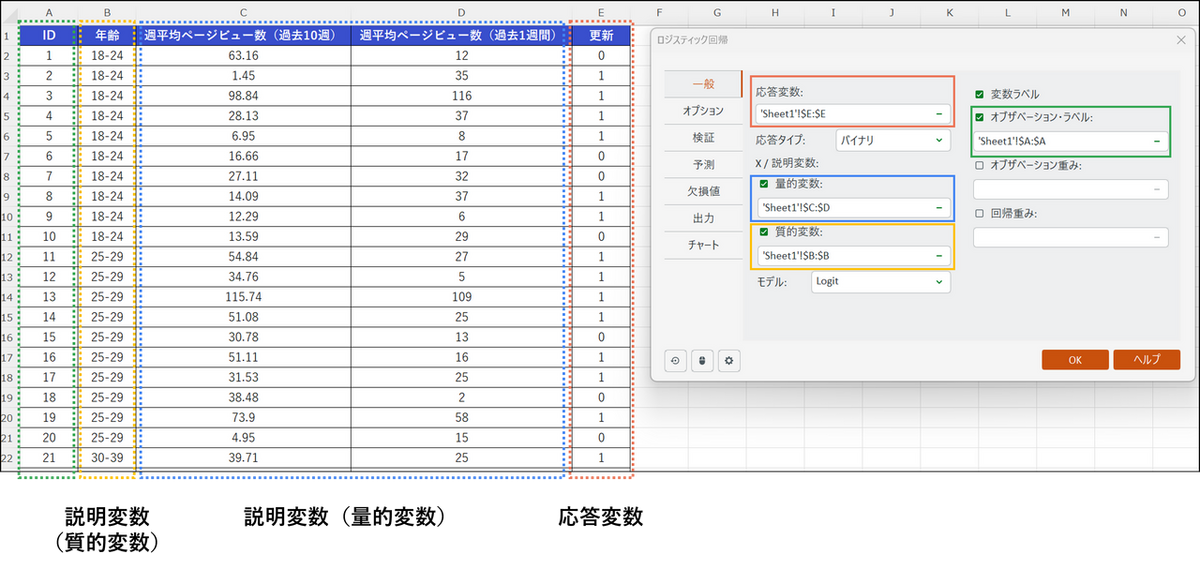
XLSTAT によるロジスティック回帰:利用状況から契約の更新有無を予測しよう
- ロジスティック回帰とは?
- 重回帰分析とロジスティック回帰分析の主な違い
- オッズとオッズ比
- ロジスティック回帰を実行するためのデータセット
- XLSTAT でロジスティック回帰を実行する手順
- ロジスティック回帰の結果の解釈
- まとめ
- 参考文献
- XLSTAT の無料トライアル
ロジスティック回帰とは?
ロジスティック回帰とは、ある出来事が起こる確率を予測し、その結果が「Yes/No」「購入/非購入」といった2つのカテゴリのどちらに分類されるかを判断するための統計手法です。例えば、「顧客が商品を買うか、買わないか」「このメールは迷惑メールか、そうでないか」といったビジネス上の課題や、「年齢、性別、閲覧履歴」といったデータから「顧客がサービスの契約を更新するかどうか」を予測したい場合に非常に有効な手法です。
重回帰分析とロジスティック回帰分析の主な違い
データ分析でよく使われる重回帰分析とロジスティック回帰分析は、どちらも複数の要因から結果を予測する点で似ていますが、その目的と仕組みに明確な違いがあります。
最も大きな違いは、何を予測したいかという点にあります。重回帰分析が予測するのは、売上高、気温、テストの点数といった連続する数値です。結果は特定の範囲内で自由に値をとることができます。一方で、ロジスティック回帰分析が予測するのは、「購入/非購入」、「合格/不合格」、「当選/落選」といったカテゴリに分類される結果です。
この目的の違いから、モデルの形も異なります。重回帰分析は、要因と結果が直線的な関係にあると仮定し、予測値を直接計算します(例:「広告費が1万円増えると、売上が5万円増える」)。これに対し、ロジスティック回帰分析は、要因と「確率」がS 字型の曲線関係にあると仮定します。これは、確率が0%以下や100%以上にならないようにするためです。モデルは直接カテゴリを予測するのではなく、まず「あるカテゴリに属する確率」を計算し、その確率に基づいて最終的な分類を行います(例:「広告をクリックする確率は75%なので、『クリックする』と予測する」)。
要約すると、数値を予測したいなら重回帰分析、結果がどのグループに属するかを確率的に予測したいならロジスティック回帰分析、と使い分けます。
| 重回帰分析 | ロジスティック回帰分析 | |
| 目的変数 | 連続値 (例:売上、気温、テストの点数) |
カテゴリ変数 (例:購入/非購入、合格/不合格) |
| モデルの形 | 直線 | S 字曲線(シグモイド関数) |
| 予測値 | 数値そのもの (例:売上は10万円になる) |
確率 (例:購入する確率は75%) |
オッズとオッズ比
ロジスティック回帰の結果を深く理解するには、「オッズ」と「オッズ比」という考え方が重要です。ここでは、その意味を一つずつ見ていきましょう。
オッズ
オッズとは、ある出来事の「起こりやすさ」そのものを示す数値です。まずは、馴染みのある「確率」から考えてみましょう。確率は、全体の中で「あるイベントが起こる割合」のことです。例えば、ここに喫煙者100人がいて、そのうち20人が病気になったとします。この場合、病気になる「確率」は20%(0.2)です。これに対して、オッズは少し視点が異なり、「病気になった人(20人)」と「病気にならなかった人(80人)」を直接比べます。計算はとてもシンプルで、「イベントが起こった数 ÷ イベントが起こらなかった数」で求めることができます。
オッズ=20人÷80人=0.25
この「0.25」がオッズです。これは「病気にならなかった人と比べて、病気になることは0.25倍起こりやすい」という意味になります。もしオッズが「1」なら「起こる数」と「起こらない数」が同じ、オッズが「4」なら「起こらない場合に比べて4倍起こりやすい」ということで、数値が大きいほど、そのイベントが起こりやすいと直感的に理解できます。
オッズ比
オッズ比とは、その名の通り「2つのグループのオッズを比べた(割り算した)値」のことです。これを使うと、「A グループはB グループに比べて、あるイベントがどれくらい起こりやすいのか?」を明確に示すことができます。先ほどの喫煙者の例に加えて、非喫煙者のデータも見てみましょう。
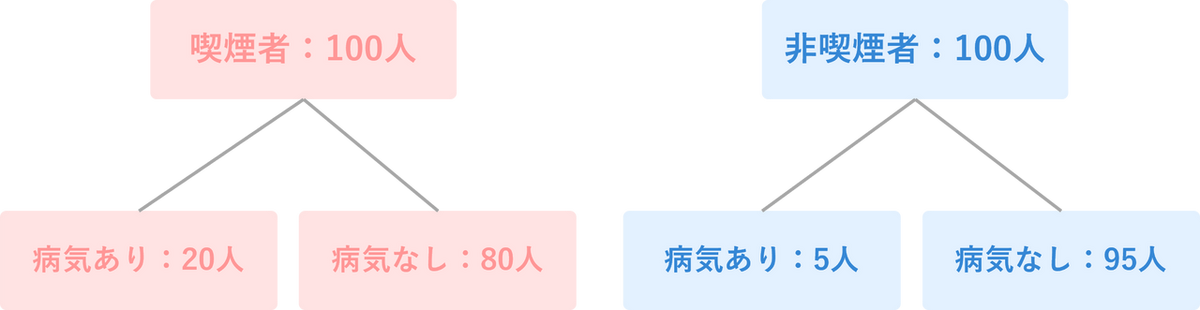
- 喫煙者グループ(100人): 病気になった人 20人、ならなかった人 80人
- 非喫煙者グループ(100人): 病気になった人 5人、ならなかった人 95人
まず、それぞれのグループのオッズを計算します。
- 喫煙者のオッズ: 20÷80=0.25
- 非喫煙者のオッズ: 5÷95≒0.053
次に、この2つのオッズを割り算して、オッズ比を求めます。

この「4.7」という数値がオッズ比です。これは「非喫煙者に比べて、喫煙者は病気になるオッズ(起こりやすさ)が約4.7倍も高い」と解釈できます。このように、オッズ比は2つのグループのリスクを比較するのに非常に便利な指標です。
ロジスティック回帰におけるオッズ比について
ロジスティック回帰分析では、ある要因が1単位増える(または、ある条件に当てはまる)と、結果が起こるオッズ(起こりやすさ)が何倍になるかをこのオッズ比で評価します。先ほどの例で言えば、年齢など他の条件の影響を調整した上で、ロジスティック回帰分析を行うと、「喫煙」という要因のオッズ比が「4.7」と計算されたりします。これは、「喫煙という習慣が、病気の起こりやすさを4.7倍にしている」という影響度を示しているのです。
このオッズ比が:
- 1より大きい場合:
その要因は、結果が起こりやすくなる「促進要因」です。(例:喫煙のオッズ比が4.7) - 1より小さい場合:
その要因は、結果が起こりにくくなる「抑制要因」です。(例:もし運動習慣のオッズ比が0.6なら、運動すると病気になるオッズが0.6倍、つまり40%低下する) - ちょうど1の場合:
その要因は、結果の起こりやすさに影響しないことを意味します。
このようにオッズ比を見ることで、「どの要因が、どれくらい結果に影響しているのか」を直感的に理解することができます。
ロジスティック回帰を実行するためのデータセット
今回は、あるオンラインサービスのユーザーデータ(60名分)を使用します。
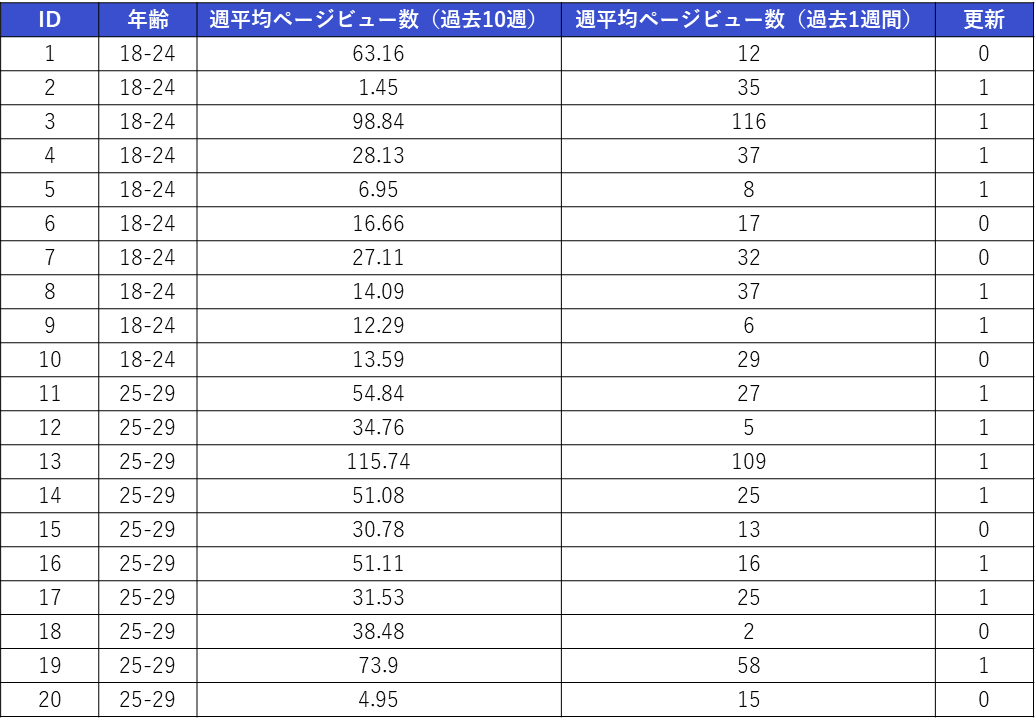
- 目的変数:
- 更新:ユーザーがサービスを更新したかどうか(1 = 更新, 0 = 更新しない)
- 説明変数:
- 年齢:ユーザーの年齢層(カテゴリー変数)
- 週平均ページビュー数(過去10週):過去10週間の週あたり平均ページビュー数(量的変数)
- 週平均ページビュー数(過去1週間):直近1週間の週あたり平均ページビュー数(量的変数)
このデータに対してロジスティック回帰分析を実行し、サービスの利用状況から、ユーザーがサービスの契約を「更新」するかどうかを予測するモデルを作成してみます。
サンプルデータのダウンロードはこちらから
dataset-for-logistic-regression.xlsmXLSTAT でロジスティック回帰を実行する手順
-
XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [ロジスティック回帰] を選択します。
-
ダイアログボックスが開いたら、[一般] タブで以下の設定を行います。
- 従属変数(応答変数):
予測したい変数。今回は「更新」のデータ列を選択します。 - 応答タイプ:[バイナリ] を選択します。
- 説明変数:
- [量的変数] にチェックを入れ、「週平均ページビュー数(過去10週)」 と「週平均ページビュー数(過去1週間)」の2列を選択します。
- [質的変数] にチェックを入れ、「年齢」の列を選択します。
- モデル:[Logit] を選択します。
- オブザベーション・ラベル(任意):
今回はチェックを入れ、「ID」列を選択します。 - 変数ラベル:
見出しの行も選択しているため、チェックを入れます。
- 従属変数(応答変数):
-
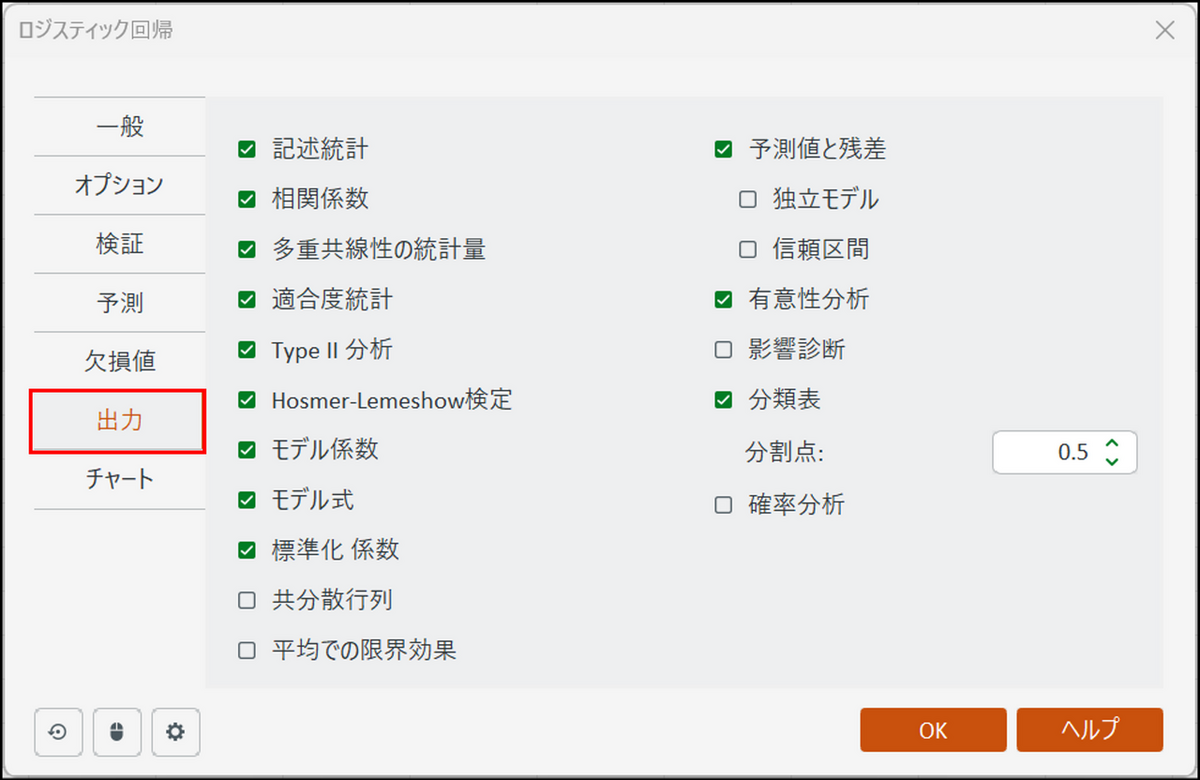
[出力] タブに切り替え、下記画面のように設定します。
-
[OK] ボタンをクリックすると、計算が始まり、結果が別シート(Log(バイナリ))に出力されます。
ロジスティック回帰の結果の解釈
ここでは、特に重要な項目について、その解釈方法を解説します。
1. 適合度統計
「適合度統計」の結果は、作成されたロジスティック回帰モデルの性能を評価するためのものです。この表では、説明変数を一切使用しない基準となるモデル(独立)と、今回作成したモデル(すべてを選択)の結果を並べて比較することで、投入した変数がモデルをどれだけ改善させたかを示しています。
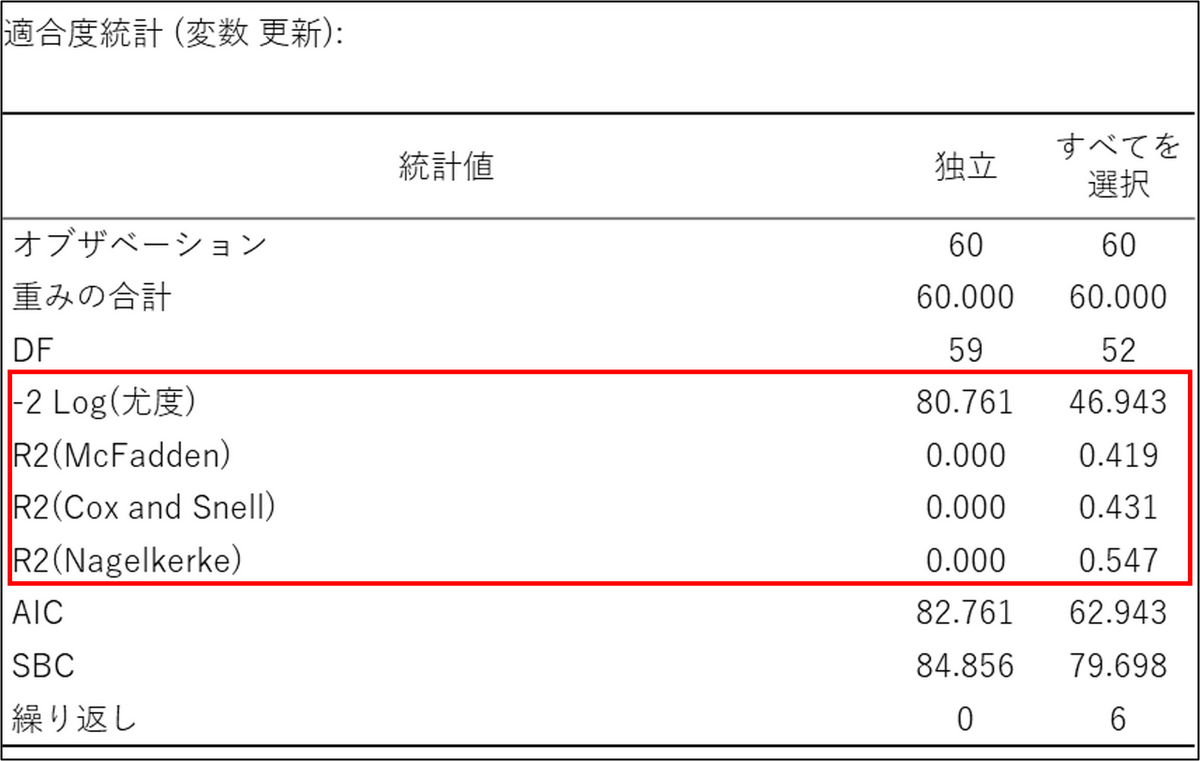
まず、注目すべき重要な指標は、モデルの当てはまりの悪さを示す「-2 Log(尤度)」(別名:逸脱度)です。これはモデルのエラーの大きさを表すスコアのようなもので、値が小さいほど性能が良いと判断されます。今回の結果では、このスコアが基準モデルの約81から、作成したモデルでは約47へと低下しています。これは、説明変数を加えたことで、モデルがデータを説明する能力が向上したことを意味しています。
次に、モデルの説明力を評価するために疑似決定係数を見ます。これを理解するには、まず通常の決定係数(R2)との違いを知ることが重要です。通常の決定係数は、売上のような数値を予測する線形回帰で用いられ、「モデルがデータ全体のばらつきの何%を説明できたか」を直接的に示します。例えば、R2 が0.7 なら、モデルが結果の70%を説明していると解釈できます。
しかし、「更新する/しない」のようなカテゴリを予測するロジスティック回帰では、結果に「ばらつき」という概念がないため、通常の決定係数は計算できません。そこで代わりに用いられるのが疑似決定係数です。これは、エラーの大きさを示す「-2 Log(尤度)」がどれだけ改善したかに基づいて計算され、通常の決定係数の役割を擬似的に果たします。結果にある 「R2(McFadden)」や「R2(Nagelkerke)」 がこれにあたり、値が0から大きく向上している(例えばNagelkerkeでは0.547)ことから、モデルが何もない状態に比べて非常に高い説明力を持つようになったと解釈できます。
以上の結果を総合すると、作成されたモデルはエラーが少なく、同時に高い説明力も持っていることが確認できます。これは、分析に用いた説明変数が統計的に非常に有効であり、信頼性の高い予測モデルが構築できたことを示しています。
【補足】疑似決定係数の種類について
XLSTATでは複数の疑似決定係数が表示されますが、それぞれ少しずつ特徴が異なります。
- R2(McFadden) - シンプルで直感的
McFadden のR2 は、「何もないモデルと比べて、モデルのエラーはどれくらい減少したか?」という改善の割合をストレートに示します。計算方法がシンプルで分かりやすいため、多くの統計ソフトで採用されている基本的な指標です。 - R2 (Cox and Snell) - R2 の考え方を応用
通常の決定係数(R2)の計算の考え方を、ロジスティック回帰に応用しようと試みた指標です。モデルの当てはまりが良いほど値が高くなりますが、この指標には「最大値が1にならない」という性質があります。 - R2 (Nagelkerke) - 最もR2 に近い感覚で使える改良版
NagelkerkeのR2 は、上記Cox and Snell のR2 を改良したものです。最大値がちょうど1になるように調整されているため、3つの中では最も通常の決定係数(R2)に近い感覚で解釈できます。
どの指標も「1に近いほど良いモデル」という点は共通しています。 まずは解釈しやすい「R2 (Nagelkerke)」 に注目し、ほかの指標も併せて確認すると、モデルの性能をより多角的に理解することができます。
2. 帰無仮説H0の検定
これは、構築したモデル全体が、切片のみのモデルと比較して、統計的に有意に優れているかどうかを検定しています。
- 帰無仮説H0:
「全ての係数(切片以外)が0である」、つまり「どの説明変数も予測に役立っていない」という仮説です。 - -2 Log(尤度) , Score, Wald:
これらは統計的な検定方法の種類です。一般的に、この中では尤度比検定 (-2 Log(尤度)) の結果が最も信頼性が高いとされています。

通常、Pr > Chi2 (p値) の値が0.05(5%)より小さい場合に「統計的に有意」と判断します。結果を確認すると、尤度比検定のp値が <0.0001 と非常に小さいため、帰無仮説は棄却されます。したがって今回作成された予測モデルは、説明変数を全く使わないモデルよりも、統計的に有意に予測精度が高く、モデル全体として意味のあるものだと判断できます。
3. Type II 分析
Type II 分析では、モデルに投入した3つの説明変数のうち、具体的にどの変数が予測に強く貢献しているのか、逆にどの変数がそれほど重要でないのかを個別に評価していきます。
この分析でも、各変数に対して「この変数は予測に役立っていない(係数が0である)」という帰無仮説を立て、p値(「Pr > Wald」や「Pr > LR」)を計算します。ここでもp値が十分に小さい(一般的に0.05未満)変数は目的変数に「有意な影響を与えている」と判断されます。

結果を確認すると、「週平均ページビュー数(過去1週間)」と「年齢」は、尤度比検定(Pr > LR)のp値がどちらも基準となる0.05を下回っており、このモデルにおいて重要な変数であることが示唆されます。一方で、「週平均ページビュー数(過去10週)」のp値は0.353と、0.05を大きく上回っています。これは、この変数をモデルに加えても、予測精度はほとんど改善しないことを意味します。したがって、このモデルの中では、「更新」という行動を予測する上で、この変数の重要度は低いと判断できます。このように、Type II 分析はモデルの「中身」を精査し、結果に影響を及ぼす要因を見つけ出すための重要な手がかりを提供してくれます。
4. Hosmer-Lemeshow検定
ホスマー・レメショウ検定(Hosmer-Lemeshow test)は、作成されたモデルの「当てはまりの良さ(適合度)」を評価するためのものです。この検定では、p値(Pr > Chi2)が非常に重要になります。

- 帰無仮説 (H₀):このモデルはデータにうまく適合している(予測と実績に差はない)
- 対立仮説 (H₁):このモデルはデータに適合していない(予測と実績に差がある)
検定のルールは以下の通りです。
- p値 > 0.05:帰無仮説は棄却されない → モデルはデータに適合していると判断します。
- p値 < 0.05:帰無仮説は棄却される → モデルはデータに適合していないと判断します。
今回表示された結果 Pr > Chi2 = 0.459 は、0.05よりも十分に大きいため、「この分析モデルはデータにうまく適合しており、その予測確率は信頼できる」と結論づけることができます。
5. モデルパラメータ
この「モデル・パラメータ」の表は、どの要因が結果(今回の場合は「更新」)に影響を与えているかを詳細に示しています。
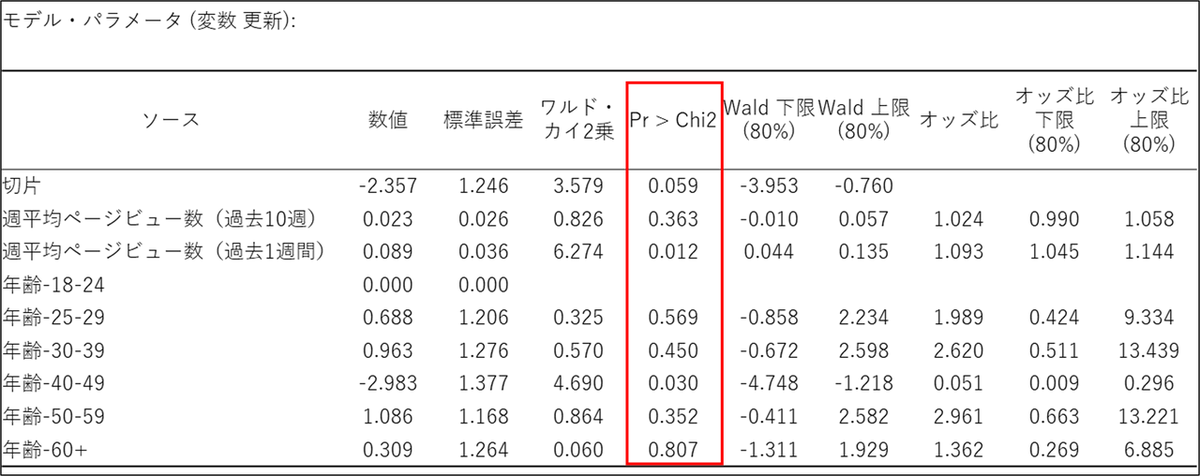
この表を解釈するには、まず各要因が統計的に意味のある影響を与えているかを見極める必要があります。その判断は「Pr > Chi2」の値を見て行います。この値が一般的な基準である0.05より小さい場合、その要因の影響は偶然ではなく、意味のあるものだと考えられます。
次に、影響が意味のあるものだと分かった要因については、オッズ比の列を確認します。オッズ比は、その要因が結果の起こりやすさを何倍にするかを示す数値です。オッズ比が1より大きい場合は、結果が起こる確率を高めるポジティブな要因であることを意味し、1より小さい場合は、確率を下げるネガティブな要因であることを示します。

今回の結果にこの解釈を当てはめてみましょう。まず、p値が0.05より小さい有意な要因は2つ見つかります。一つは「週平均ページビュー数(過去1週間)」で、p値は0.012です。この要因のオッズ比は1.093となっており、これは直近1週間のページビュー数が1増えるごとに、更新する確率が1.093倍(約9.3%)高まることを意味します。つまり、直前の活動が活発であるほど、更新につながりやすい傾向があると言えます。
もう一つの有意な要因は「年齢-40-49」で、p値は0.030です。こちらのオッズ比は0.051と1を大きく下回っており、強いネガティブな影響を示しています。これは、基準となる年齢層(18-24歳)と比較して、40-49歳の人は更新する確率が0.051倍にまで減少する、つまり約95%も低くなることを表しています。この年齢層は、他の層に比べて更新しない傾向が際立っていることが分かります。
一方で、ここに記載されている他の要因、例えば「週平均ページビュー数(過去10週)」や40-49歳以外の年齢層は、p値が0.05を上回っています。これは、今回のデータにおいては、これらの要因が更新に与える影響は統計的に明確ではなく、観測された差が偶然である可能性を否定できないことを示唆しています。
この結果から、サービスの更新確率を高めるためには、直近1週間のユーザー活動を促すことが重要であり、特に40-49歳のユーザー層がなぜ更新に至らないのか、その理由を探ることが次のアクションに繋がるかもしれません。
6. 予測値と残差
「予測値と残差」の表は、データの一つひとつ(各オブザベーション)について、実際の答えとモデルの予測を比較しています。これにより、モデルがどのようなケースを得意とし、どのようなケースを苦手とするのかを具体的に見ることができます。
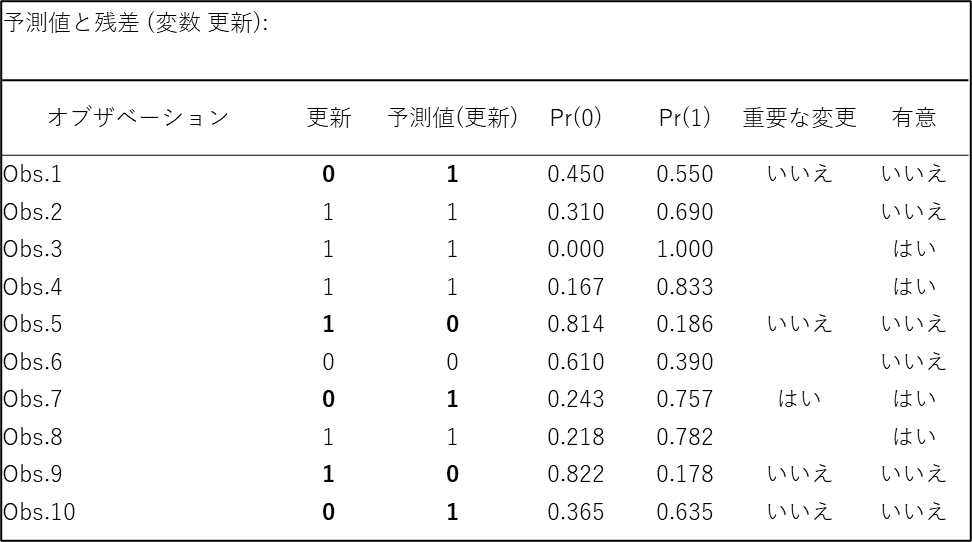
各列の意味を理解することで、簡単に解釈できます。
- 更新列:
「実際の答え」です。1は実際に更新した人、0は更新しなかった人を示します。 - 予測値(更新) 列:
「モデルが出した予測」です。モデルが「この人は更新するだろう」と判断すれば1、「しないだろう」と判断すれば0になります。 - Pr(0) と Pr(1) 列:
モデルが予測を出す根拠となった確率です。Pr(1)は「更新する確率」、Pr(0)は「更新しない確率」です。モデルは通常、Pr(1)が50% (0.5) を超えていれば予測を1、下回っていれば0とします。
実際に表のデータを見てみましょう。
- Obs.2(予測成功例)
- 実際の答え (更新): 1 (更新した)
- モデルの予測 (予測値): 1 (更新すると予測)
モデルは、この人が更新する確率を69% (Pr(1)=0.690) と計算しました。50%を超えているため「更新する」と予測し、結果的に正解しています。
- Obs.5(予測失敗例)
- 実際の答え (更新):1 (更新した)
- モデルの予測 (予測値): 0 (更新しないと予測)
モデルは、この人が更新する確率をわずか18.6% (Pr(1)=0.186) と計算しました。50%を下回ったため「更新しない」と予測しましたが、実際には更新しており、これは予測の誤りです。
- 重要な変更 / 有意列
これらの列は、特に注目すべきケースに「はい」などのフラグを立てます。例えば Obs.7 は、実際は0(更新せず)でしたが、モデルは75.7%という高い確率で1(更新する)と自信を持って間違えてしまいました。逆に Obs.3 は、100%の確率で1(更新する)と予測し、完璧に正解しています。このように、予測と実績が大きく乖離しているケースや、モデルが予測に非常に自信を持っているケースを示し、モデルの改善点を探る手がかりとします。
7. 分類表
この表は、分類表または混同行列と呼ばれるもので、作成したモデルの「予測精度」を評価するための成績表です。結論から言うと、このモデルは全体として78.33%の正解率を持っており、特に「更新した人」を正しく予測するのが得意なモデルであると言えます。
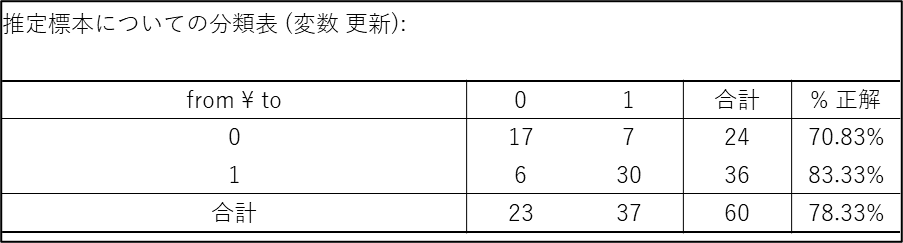
- 行 (from):実際の答え(本当に更新したか・しなかったか)
- 列 (to):モデルの予測(モデルが更新すると予測したか・しないと予測したか)
表の数字を一つずつ見ていくと、モデルの性能がよく分かります。
- 左上の「17」:
実際に更新しなかった人(from 0)を、正しく「更新しない(to 0)」と予測できた数。 - 右下の「30」:
実際に更新した人(from 1)を、正しく「更新する(to 1)」と予測できた数。
これら斜めのライン(17と30)が、予測が当たった数(正解数)です。
- 右上の「7」:
実際は更新しなかった人(from 0)を、間違って「更新する(to 1)」と予測してしまった数(間違い①)。 - 左下の「6」:
実際は更新した人(from 1)を、間違って「更新しない(to 0)」と予測してしまった数(間違い②)。 - 全体の正解率(78.33%):
合計60人のうち、正解したのは17 + 30 = 47人です。したがって、モデル全体の正解率は 47 ÷ 60 = 78.33% となり、まずまずの精度を持っていると言えます。
- クラスごとの正解率:
- 更新しなかった人 (from 0):
24人中17人を正しく予測できており、正解率は 70.83% です。 - 更新した人 (from 1):
36人中30人を正しく予測できており、正解率は 83.33% です。
- 更新しなかった人 (from 0):
この結果から、このモデルは「更新しない人」を予測するよりも、「更新する人」を予測する方が得意であることが分かります。ビジネスの目的によっては(例えば、更新しそうな人にアプローチしたい場合など)、非常に有用なモデルだと言えるでしょう。
8. 混同プロット
混同プロットは一つ前の「分類表(混同行列)」をグラフで可視化したものです。モデルの予測精度を、数字の表だけでなく直感的に把握するために使われます。
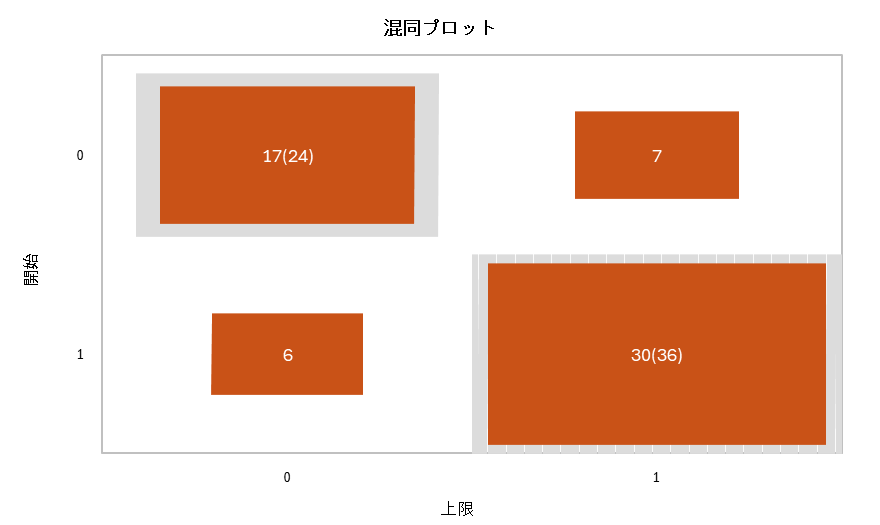
このグラフは、モデルの「答え合わせ」の結果を示しています。
- 縦軸(開始):
実際の答えを表します。(0 = 更新しなかった, 1 = 更新した) - 横軸(上限):
モデルの予測を表します。(0 = 更新しないと予測, 1 = 更新すると予測)
正解した部分(グレーの枠で囲まれた対角線)
- 左上の箱 17(24):
実際に更新しなかった(開始=0) 24人のうち、17人を正しく「更新しない(上限=0)」と予測できたことを示します。 - 右下の箱 30(36):
実際に更新した(開始=1) 36人のうち、30人を正しく「更新する(上限=1)」と予測できたことを示します。
このグレーで囲まれた対角線上の箱が大きいほど、モデルの精度が高いことを意味します。
間違えた部分(グレーの枠で囲まれた対角線以外の箱)
- 右上の箱 7:
実際は更新しなかった(開始=0)のに、間違って「更新する(上限=1)」と予測してしまった人数です。 - 左下の箱 6:
実際は更新した(開始=1)のに、間違って「更新しない(上限=0)」と予測してしまった人数です。
このグレーの枠で囲まれた対角線以外の箱が小さいほど、モデルの間違いが少ないことを示します。
9. 分類性能指標(GCI)
分類性能指標の表は、作成したモデルの予測性能が全体としてどれくらい良かったかを評価します。ここでは、モデルの性能を示す4つの重要な指標を確認できます。

- % 正解
モデルが正しく分類できたデータの割合です。「更新する」と予測した人が本当に更新しており、「更新しない」と予測した人が本当に更新しなかった、というケースが全体の何パーセントあったかを示します。この数値が高いほど、モデルの正解率が高いことを意味します。
- % 不確実
モデルが「どちらとも判断できなかった」データの割合です。これはXLSTAT の「有意性分析」オプションを有効にしている場合に表示される特別な指標です。モデルが算出した確率が、更新する・しないの境目に近く、自信を持って答えを出せなかったケースがここに分類されます。この数値が高い場合は、モデルが判断に迷っているケースが多いことを示唆します。
- % 誤分類
モデルが自信を持って予測したものの、その予測が間違っていたデータの割合です。「更新する」と予測したのに実際は更新しなかった(またはその逆)という、明確な間違いが全体の何パーセントあったかを示します。
- GCI (Goodness of Classification Index)
「分類の良さの指標」を意味し、モデルの性能を評価する最終的な総合スコアです。これはXLSTAT 独自の指標で、上記の「正解」「不確実」「誤分類」の3つのバランスを考慮して算出されます。モデルの予測品質を現実的に評価するための指標であり、このスコアを見ることで、モデル全体の性能を一つの数値で把握することができます。GCI スコアの目安は以下の通りです。- 70%以上:良いスコア
- 50%:平均的なスコア
- 50%未満:予測品質が低いスコア
今回の結果 67.50% は、平均よりは良いものの、「良いモデル」の基準である70%には一歩及ばない、まずまずの結果と言えます。これは、「% 不確実」が高かったことが影響しています。
【補足】各指標の計算方法
3つの指標は、「分類性能指標(GCI)」の上に表示される「不確実」を含む特別な分類表の数値を基に計算されます。それぞれの指標は、該当するカテゴリのデータ数を全体のデータ数で割り算して、パーセント(%)に直したものです。

- % 正解 の計算
(% 正解) = (正解数 / 総データ数) * 100
モデルが「正解」を出した割合です。
計算例:(24 / 60) * 100 = 40.00% - % 不確実 の計算
(% 不確実) = (不確実数 / 総データ数) * 100
モデルが判断を保留し、「不確実」とした割合です。
計算例: (35 / 60) * 100 = 58.33% - % 誤分類 の計算
(% 誤分類) = (誤分類数 / 総データ数) * 100
モデルが「不正解」を出した割合です。
計算例: (1 / 60) * 100 = 1.67%
10. ROC 曲線
このグラフはROC曲線と呼ばれ、モデルの性能を視覚的に評価するためのものです。モデルがどれだけうまく2つのグループ(今回は「更新する」と「しない」)を区別できるかを示しています。
参考:XLSTAT によるROC 曲線:検査性能を評価しよう
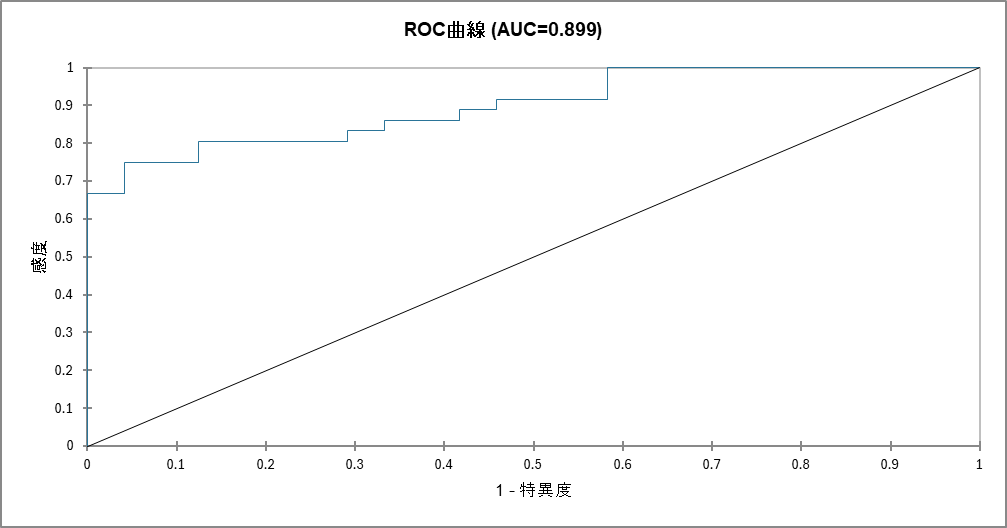
- 縦軸(感度):
本当に更新した人を、正しく「更新する」と予測できた割合(見逃しの少なさ)。 - 横軸(1 - 特異度):
本当は更新しなかった人を、間違って「更新する」と予測してしまった割合(間違いの多さ)。
ROC 曲線では下記2つのポイントを確認して解釈します。
1. 曲線の形
理想的なモデルの曲線は、グラフの左上に大きく膨らみます。これは、「間違い」を少なく保ちながら、多くの「正解」を当てられている状態を意味します。今回の結果でも青い線は、左上に大きく張り付くように描かれています。これは、モデルが非常に高い精度で予測できていることを示しています。グラフの中央を斜めに走る直線は「ランダムに当てずっぽうで予測した場合」の性能なので、それよりも遥かに優れたモデルであることが一目で分かります。
2. AUC スコア
AUC(Area Under the Curve)は、このROC 曲線の下の面積を0から1の数値で表したものです。モデルの性能を一言で表す総合スコアであり、1に近いほど性能が良いことを意味します。
- AUC = 1.0:完璧なモデル
- AUC = 0.5:ランダムな予測と同じレベル(役に立たない)
今回のモデルのAUC スコアは0.899であり、非常に信頼性が高いと言えます。
まとめ
ロジスティック回帰分析は、「ある結果」に対して「どの要因が、どの程度影響しているか」を統計的に明らかにし、データに基づいた客観的な意思決定を可能にする非常に有用な手法です。今回の分析では、作成した予測モデルはデータによく適合し、ユーザー行動の約55%(NagelkerkeのR2)を説明し、全体の正答率も78.33%という精度の高い結果を示しました。特にサービスの更新を予測する上で重要だったのは、「直近1週間の利用頻度」と「40-49歳であること」でした。この結果から、アクティブなユーザーの利用を促す施策が有効である可能性や、40-49歳のユーザーが更新しない理由を調査する必要性といった、具体的なアクションへのヒントが得られます。このように、データに隠されたビジネスチャンスや課題を簡単に見つけ出すために、使い慣れたExcel 上で高度な分析が可能なXLSTAT をぜひご活用ください。
参考文献
- XLSTAT: Binary logit model in Excel
https://community.lumivero.com/s/article/6432-binary-logit-model-excel?language=en_US - FAQ: How are the likelihood ratio, Wald, and Lagrange multiplier (score) tests different and/or similar?
https://stats.oarc.ucla.edu/other/mult-pkg/faq/general/faqhow-are-the-likelihood-ratio-wald-and-lagrange-multiplier-score-tests-different-andor-similar/ - 新谷歩: みんなの医療統計 多変量解析編 10日間で基礎理論とEZRを完全マスター!, 講談社, 2017.
XLSTAT の無料トライアル
トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介したロジスティック回帰分析はすべてのライセンスでご利用いただけます。
無料トライアルを申し込む*トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。