XLSTAT による単回帰分析:身長から体重を予測してみよう
回帰分析とは?
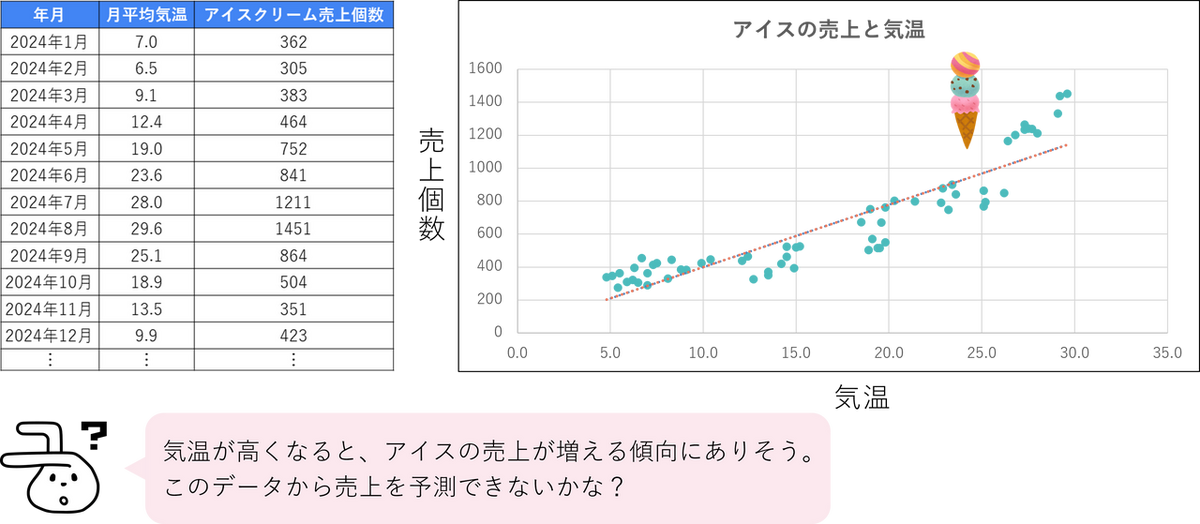
回帰分析とは、ある変数(原因)が、別の変数(結果)にどの程度影響を与えるかを数式で明らかにする統計手法です。回帰分析では、例えば「気温が1度上がると、アイスの売上は50個増える」のように、2つの変数の関係性を「予測モデル」という一本の数式で表します。このモデルがあれば、手元にあるデータ(原因)から、まだわからないデータ(結果)を予測できるようになります。

なお、回帰分析では、扱う変数を役割に応じて次のように呼びます。
- 説明変数
予測の「原因」となる変数です。独立変数とも呼ばれます。
(例:気温、広告費、勉強時間、身長) - 目的変数
説明変数の影響を受ける「結果」にあたる変数です。予測したい対象の変数です。従属変数とも呼ばれます。
(例:アイスの売上、サイトの売上、テストの点数、体重)
説明変数と目的変数の例
| 説明変数 | 目的変数 | 分析の目的 |
| 気温 | アイスの売上 | 気温の変化が売上に与える影響を分析する |
| 広告費 | 製品売上 | 広告投資が売上向上にどの程度寄与するかを分析 |
| 勉強時間 | テストの点数 | 勉強時間が成績にどう関係するかを把握する |
| 身長 | 体重 | 身長から体重を推定し、健康指標に活用する |
つまり、回帰分析は「説明変数が変化すると、目的変数がどれくらい変化するのか?」という関係性を解き明かす手法と言えます。
回帰分析の種類
回帰分析には、データの関係性の形によっていくつかの種類があります。
線形回帰
変数の関係を「直線」で表せると考える、最もシンプルでよく使われるタイプです。線形回帰では2つの変数の関係を一次関数「y = ax + b」の形で表現し、予測モデルを作成します。
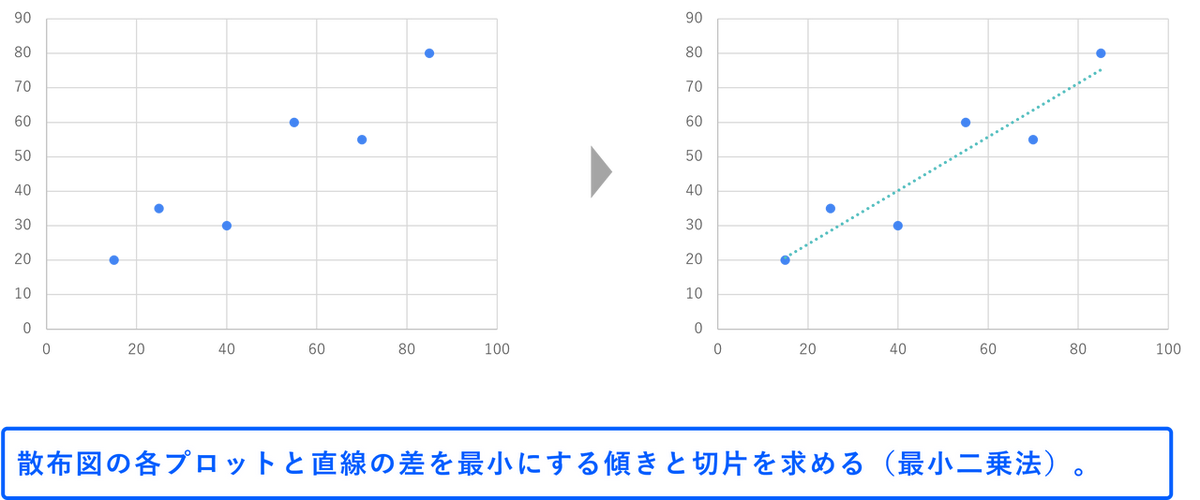

線形回帰分析は、大きく分けて「単回帰分析」と「重回帰分析」に分けられます。
- 単回帰分析
1つの説明変数から1つの目的変数を予測します(例: 「身長」だけで「体重」を予測する)。 - 重回帰分析
複数の説明変数から1つの目的変数を予測します(例: 「身長」と「年齢」と「性別」から「体重」を予測する)。
単回帰分析より、さらに精度の高い予測が期待できます。
非線形回帰
非線形回帰とは、データ間の関係が直線ではない場合に、その関係を数学的な曲線で表現する回帰分析の手法です。現実世界の現象は、必ずしも単純な直線関係で説明できるわけではありません。非線形回帰は、そのような複雑な関係をより正確にモデル化するために利用されます。
このページでは線形回帰のうち説明変数が1つである単回帰分析をXLSTAT で実行する方法をご紹介します。
単回帰分析を実行するためのデータセット
今回は237人の子どもの身体測定データを使って、「身長から体重を予測する」単回帰分析を実行します。子どもの成長は厳密には曲線を描きますが、ある一定の年齢層を切り取れば、直線に近い関係と見なして分析できます。

サンプルデータのダウンロードはこちらから
sample-data-for-simple-linear-regression.xlsmXLSTAT で単回帰分析を実行する手順
-
XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [線形回帰] を選択します。
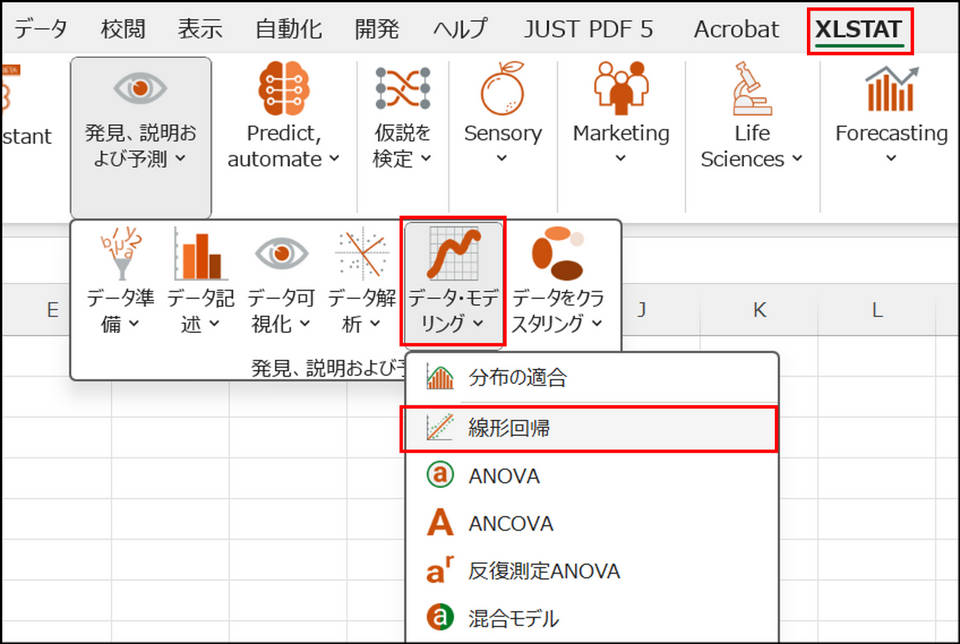
-
ダイアログボックスが開いたら、[一般] タブで以下の設定を行います。
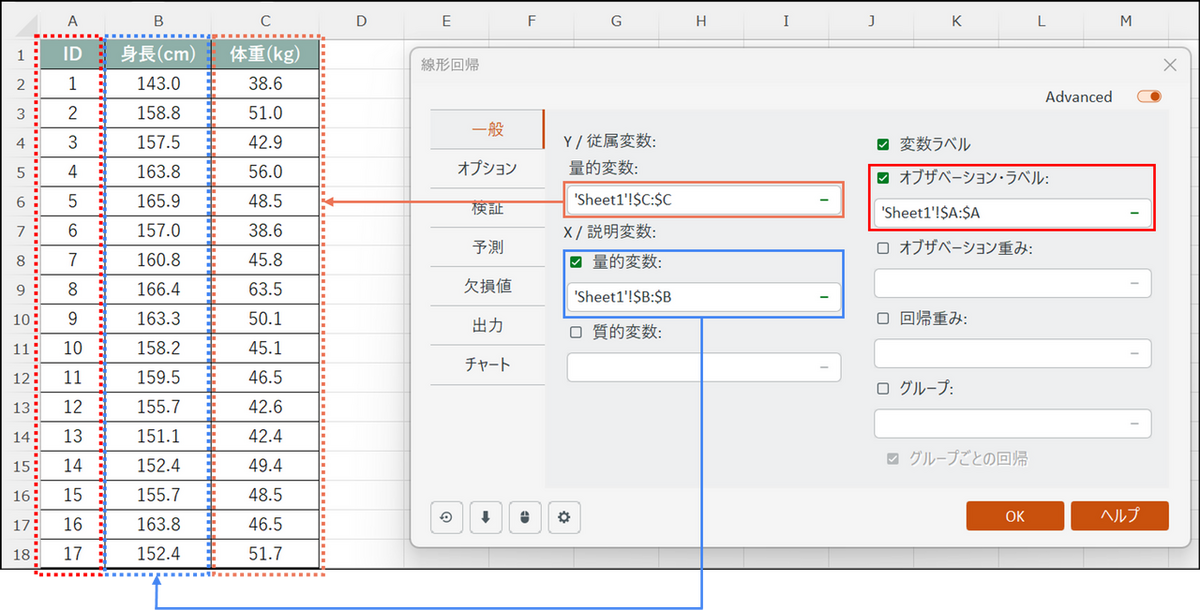
- 従属変数:
予測したい変数。今回は「体重(kg)」のデータ列を選択します。 - 説明変数:
[量的変数] にチェックを入れ、「身長(cm)」のデータ列を選択します。 - オブザベーション・ラベル(任意):
今回はチェックを入れ、「ID」列を選択します。
- 従属変数:
-
[出力] タブに切り替え、[予測値と残差] の項目にチェックを入れます。
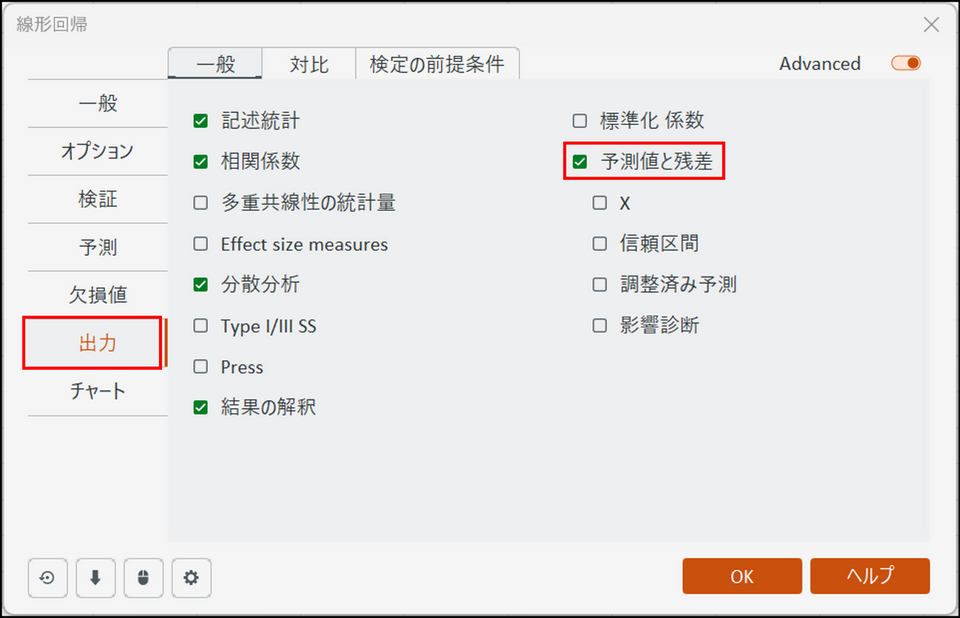
-
[OK] ボタンをクリックすると、計算が始まり、結果が別シート(線形回帰)に出力されます。
単回帰分析の結果の解釈
結果には様々な指標が出力されますが、以下の項目を確認することで基本的な情報は得られます。
適合度統計
適合度統計ではモデルの適合度を示す係数が表示されます。特に重要なのは、「R2(決定係数)」という値です。これは選択した説明変数(身長)のみで、どれくらい結果(体重)を説明できているのかを示しており、値が1に近いほど、モデルの当てはまりが良いことを意味します。
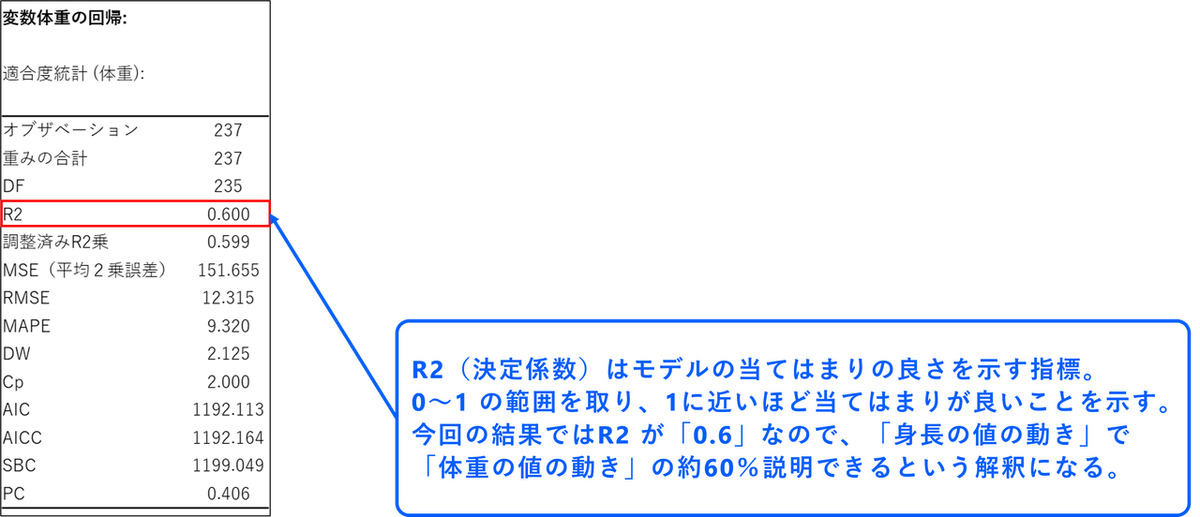
今回の結果では、R2 が約0.6でした。これは、体重のばらつきの60%が身長によって説明できることを示しています。残りの40% のばらつきは、この分析には含まれていない他の要因(年齢や性別など)によるものと考えられます。R2 の値は0から1の範囲を取ります。一般的に、R2 の値が0.8 以上あれば予測性能が高くて良いモデルと言われていますが、いくつ以上でないとならないという決まりはありません。モデルの予測性能を評価する指標として理解しておきましょう。
分散分析
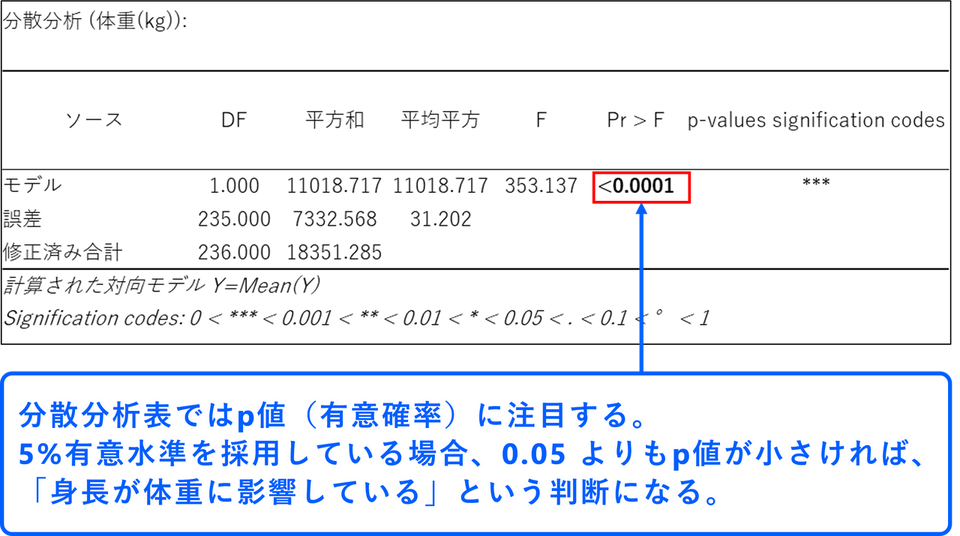
分散分析の結果では説明変数(身長)がモデルに対して意味のある情報をもたらしているかどうかを確認できます。今回の事例では分散分析表内のp値が0.0001 未満と非常に小さいため、身長という変数は、体重を予測する上で統計的に有意な情報をもたらしているという判断になります。
モデルの係数
モデル・パラメータの表では「説明変数(身長)」と「切片」の数値(係数)を確認します。係数とは、ある変数(説明変数)が目的変数(体重)にどの程度影響を与えるかを示す数値のことです。今回はそれぞれ、「0.682」と「- 60.324」となっていますので、体重(y)と身長(x)の関係は「y = 0.682x - 60.324」と直線の式で表せることになります。この式から分析対象の身長範囲において、身長(x)が1 cm 増加すると、体重(y)が0.682 kg 増加すると予測できることがわかります。なお、「切片」は説明変数(x) が0 のときの、目的変数(y)の予測値を意味します。

このようにデータから「y(体重)= 0.682x(身長) - 60.324」という具体的な計算式を求めることができれば、x に身長の値を代入することで結果の予測が可能になります。
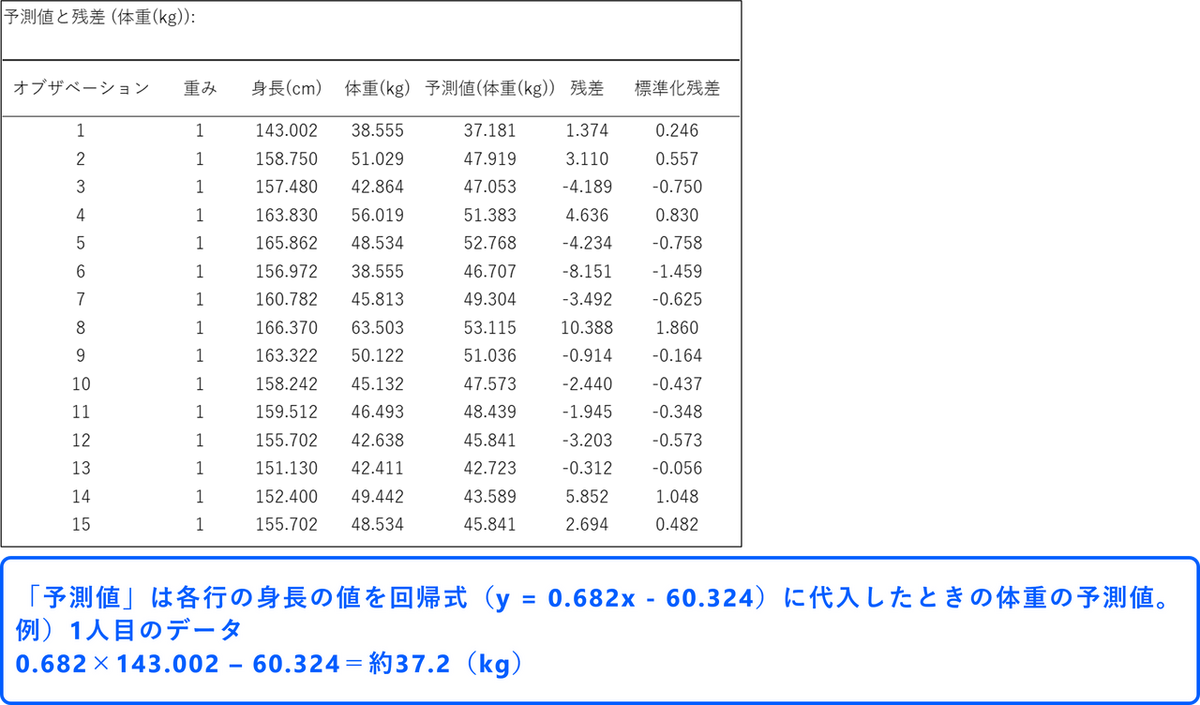
予測値と残差
「予測値と残差」の表では残差(実測値と予測値の差)を確認することができます。残差は、もとのデータの件数分出力されます。今回はもとのデータが237件あるので、237行分の結果が表示されています。「オブザベーション」には、選択したオブザーベーション・ラベル列の内容がそのまま表示されます(今回の例ではID番号が表示されています)。「予測値」には各行の身長の値を回帰式(y = 0.682x - 60.324)に代入したときの値が表示されます。「残差」は実測値から予測値を引いた値で、予測のズレを示しています。たとえば、一人目のデータであれば体重は「38.555」ですが、回帰式によって算出された予測値は「37.181」なので、残差が「1.374」です。つまり実際には予測値よりも1.374 kg 体重が重かったということになります。
【補足】
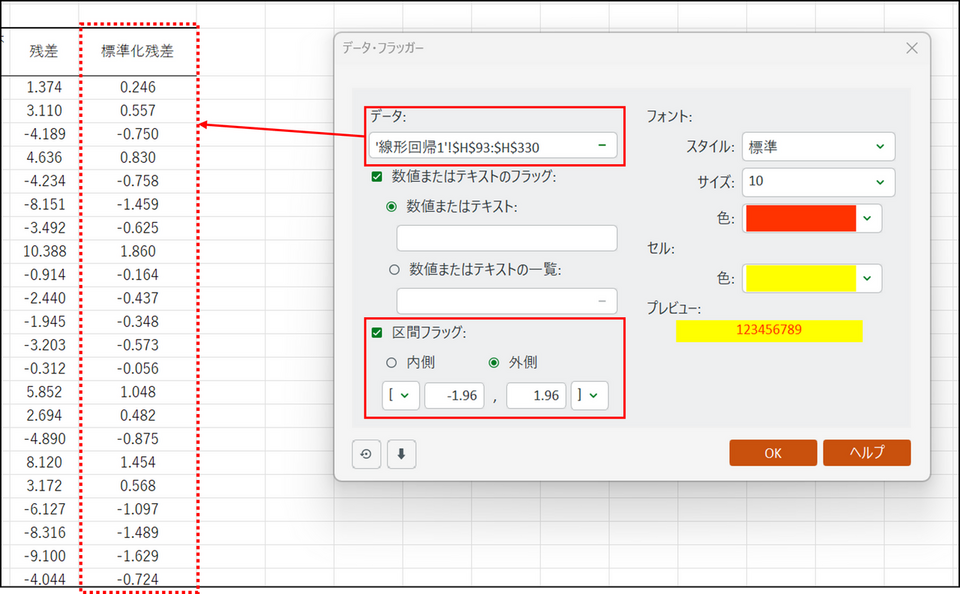
線形回帰モデルの仮定では、残差は正規分布に従うとされており、その場合、残差の95%は[-1.96〜1.96] の範囲に収まります。この範囲外の値は、外れ値である可能性や、正規性の仮定が満たされていない可能性を示唆します。XLSTAT のデータ・フラッガー機能(ツールメニュー内)を使うと、[-1.96〜1.96] の範囲外の残差を簡単に見つけ出せます。
1. XLSTAT メニュー内の[ツール] > [データ・フラッガー] を選択
2. 表示されるダイアログ画面にて以下のように指定し、[OK] をクリック
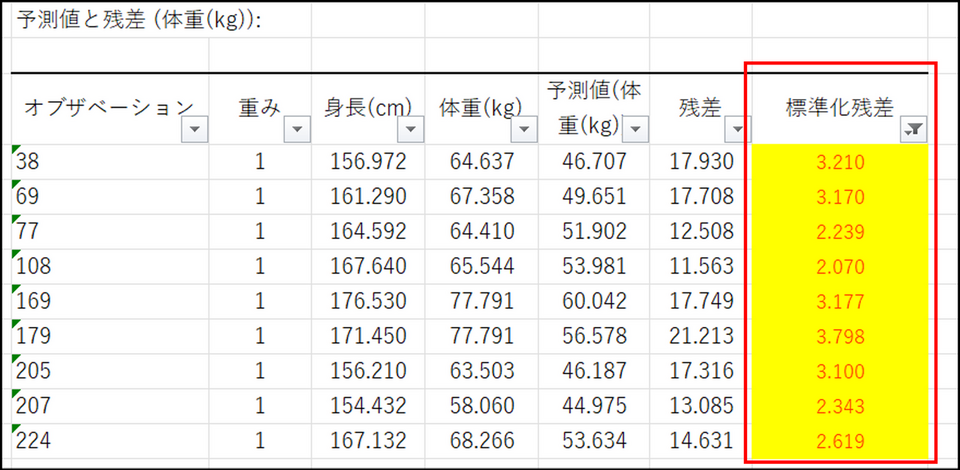
今回のデータでは237件のデータのうち9件の残差がこの範囲外にありますが、この程度であれば、正規性の仮定を棄却するほどではありません。
回帰プロット
回帰プロットでは散布図に回帰直線が重ねて表示されています。回帰プロットをみることで、2つの変数の関係性とモデルの当てはまりの良さを視覚的に確認できます。ほとんどの点が回帰直線のすぐ近くに位置していれば、そのモデルは当てはまりが良いと判断できます。また回帰プロットには2種類の区間が回帰直線の上下に表示されます。
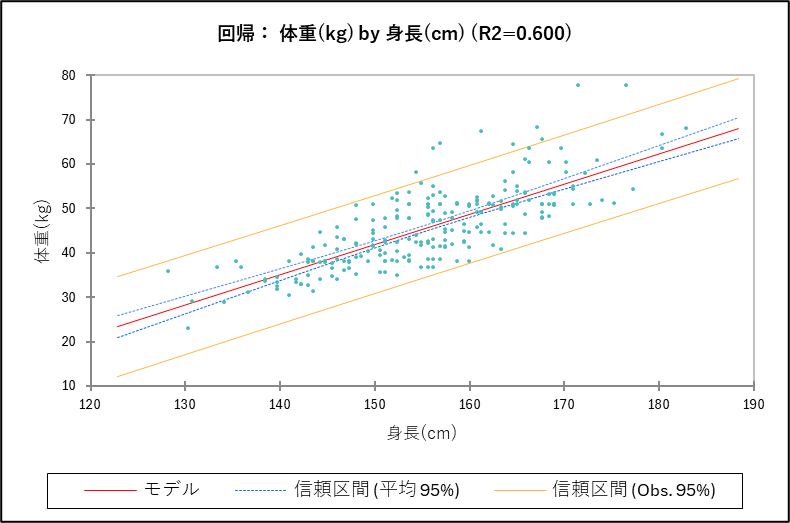
※信頼区間と予測区間の区別がつくように、直線とプロットの色を変更しています。
- 95%信頼区間(※グラフでは「信頼区間(平均95%)」と表示)
直線に近い方の細い区間は「予測値の平均の信頼区間」です。「もし同じ条件で何度も観測を繰り返したら、その結果の平均値は95%の確率でこの範囲に入る」ということを示しています。
- 95%予測区間(※グラフでは「信頼区間(Obs.95%)」と表示)
外側の広い区間は「個々の予測値の信頼区間」です。予測区間は、得られるデータの95%が含まれる範囲を示しています。これにより「新しい個々のデータ点がどの範囲に収まるか」を予測することができます。
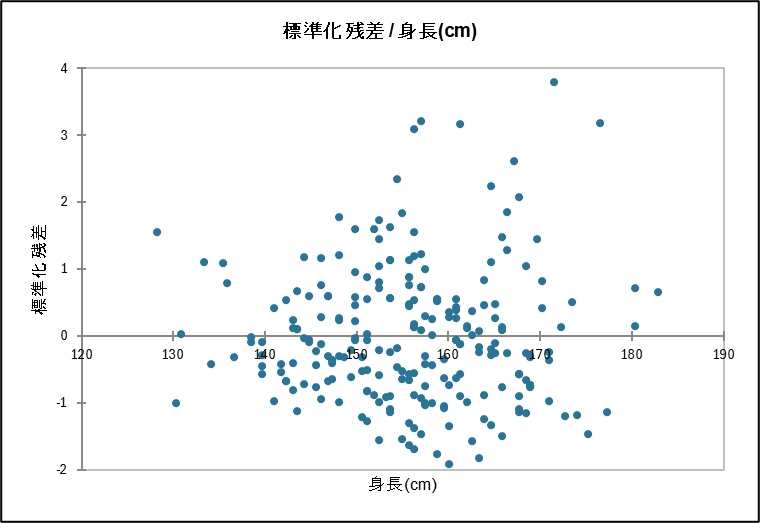
残差プロット
残差プロットは、予測モデルの残差を可視化したグラフで、横軸に説明変数(身長)、縦軸に残差(実際の値 - 予測値)がプロットされています。残差プロットの目的は、予測のズレ(残差)に何らかのパターンがないかを確認することです。もしモデルが適切であれば、予測のズレは特定の傾向を持たず、ランダムに発生するはずです。もし何らかの傾向(例えば、右上がりやU 字型など)が見られる場合、モデルが不適切であるか、残差に自己相関が存在することを示しています。今回の例では、特に明確な傾向は見られないため、モデルがデータの傾向をうまく捉えられているようです。
予測値と観測値のプロット
このグラフは、モデルによる予測値と実際の観測値をプロットし、両者の一致度を視覚的に評価するためのものです。点が対角線(y=x)上に近いほど、モデルの予測精度が高いことを示します。対角線から大きく離れている点は、予測誤差が大きいデータであり、外れ値の可能性もあります。
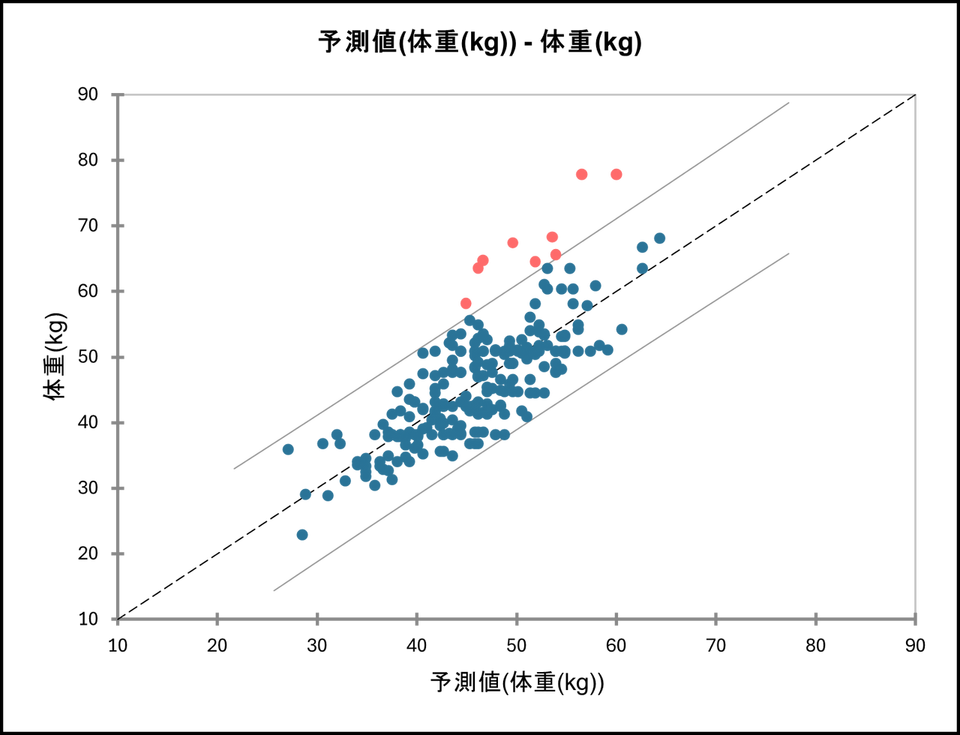
※外れ値をわかりやすくするため、プロットの色を一部変更しています。
標準化残差のヒストグラム
このヒストグラムによって、[-1.96〜1.96] の範囲から外れている残差を素早く視覚的に確認できます。
まとめ
回帰分析は、説明変数(原因)と目的変数(結果)の関係を数式で表し、未知のデータを予測するための手法です。このページでご紹介した単回帰分析は、もっともシンプルな線形回帰で、1つの原因から1つの結果を予測するために利用します。今回の分析では、身長が体重を予測するのに役立つことがわかりました。XLSTAT を使うことで、エクセル上で簡単に単回帰分析を実行し、多様な結果を取得することができます。さらに精度を高めたい場合は、年齢や性別などの別の変数を追加する「重回帰分析」へとステップアップしていくと良いでしょう。
参考文献
- XLSTAT: Simple Linear Regression in Excel
https://community.lumivero.com/s/article/6705-simple-linear-regression-excel-tutorial?language=en_US\ - 阿部真人: データ分析に必須の知識・考え方 統計学入門 仮説検定から統計モデリングまで重要トピックを完全網羅, ソシム, 2021.
- 豊田 裕貴: Excelで学ぶ 実践ビジネスデータ分析, オデッセイ コミュニケーションズ, 2023.
XLSTAT の無料トライアル
トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した単回帰分析はすべてのライセンスでご利用いただけます。
無料トライアルを申し込む*トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。



