• 重回帰分析とは？
• 重回帰分析を実行するためのデータセット
• XLSTAT で重回帰分析を実行する手順
• 重回帰分析の結果の解釈
• まとめ
• 参考文献
• XLSTAT の無料トライアル

重回帰分析とは？

重回帰分析とは、2つ以上の説明変数（原因） を使って、1つの目的変数（結果） の変動を予測・説明する統計手法です。

• 目的変数：予測したいこと（例：店舗の売上高）
• 説明変数：予測に使う要因（例：接客、品揃え、店舗の売場面積、駅からの距離）

単回帰分析が1つの原因と結果の関係（例：身長と体重）しか見られないのに対し、重回帰分析は複数の要因が絡み合う複雑な現象を分析するのに適しています。この分析を通じて、以下のようなことが可能になります。

• 売上に最も影響を与える要因を特定する
• 各要因が売上をどれくらい増減させるかを数値化する
• 新しい店舗の売上を予測するモデル（予測式）を作成する

この分析は、ビジネスから学術研究まで幅広い分野で活用されています。具体的には、以下のような場面で役立ちます。

分野	説明変数	目的変数	分析の目的
マーケティング	テレビCM 広告費、Web 広告費、SNS 広告費	売上	各広告チャネルが売上に与える貢献度を数値化し、最適な広告予算の配分を検討する。
商品開発	機能の評価、デザインの評価、価格	顧客満足度	顧客満足度に最も影響を与える要素を特定し、製品改善や次期モデル開発の優先順位を決定する。
人事	研修時間、経験年数、労働環境の評価	従業員のパフォーマンス（人事評価スコアなど）	パフォーマンス向上に寄与する要因を明らかにし、効果的な人材育成プログラムや職場環境の改善策を立案する。
医療研究	年齢、生活習慣（喫煙、飲酒、運動量など）、遺伝的要因	疾患のリスク（発症率など）	特定の疾患に対する各リスクファクターの影響度を評価し、予防医療や治療方針の策定に役立てる。

このページでは、XLSTAT を使って重回帰分析を実行し、その結果を解釈するまでの手順を分かりやすく解説します。なお、単回帰分析の詳細については下記ページをご参照ください。

XLSTAT による単回帰分析：身長から体重を予測してみよう

重回帰分析を実行するためのデータセット

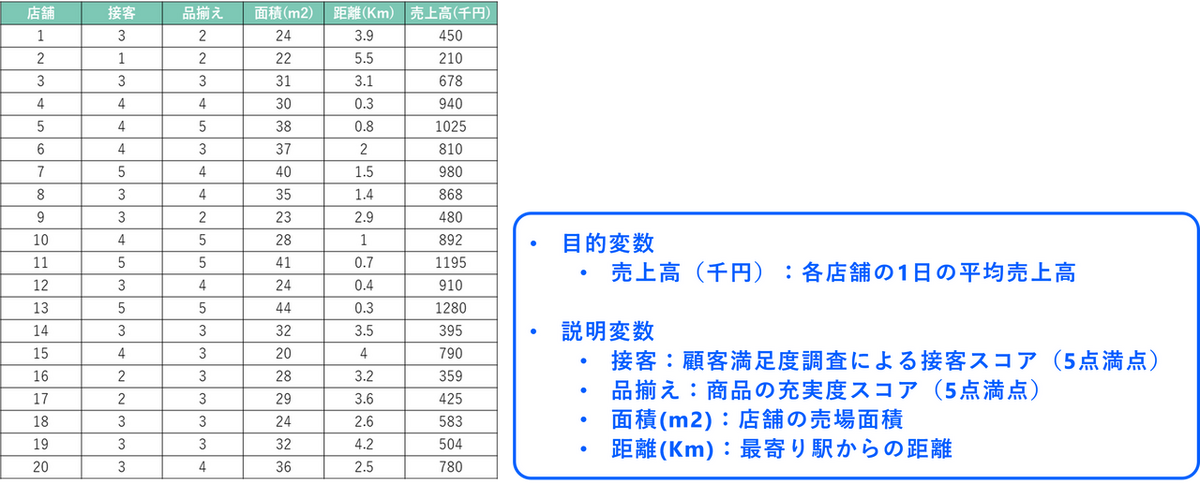
今回は、あるコンビニチェーン50店舗のデータがまとめられた以下のデータセットを使用します。

このデータに対して重回帰分析を実行することで、「接客態度」「品揃え」「店舗の広さ」「駅からの距離」のうち、どの要因がどのくらい売上に影響を与えているのかを統計的に明らかにし、将来の売上を予測するモデルを作成します。

サンプルデータのダウンロードはこちらから

sample-data-for-multi-linear-regression.xlsm

XLSTAT で重回帰分析を実行する手順

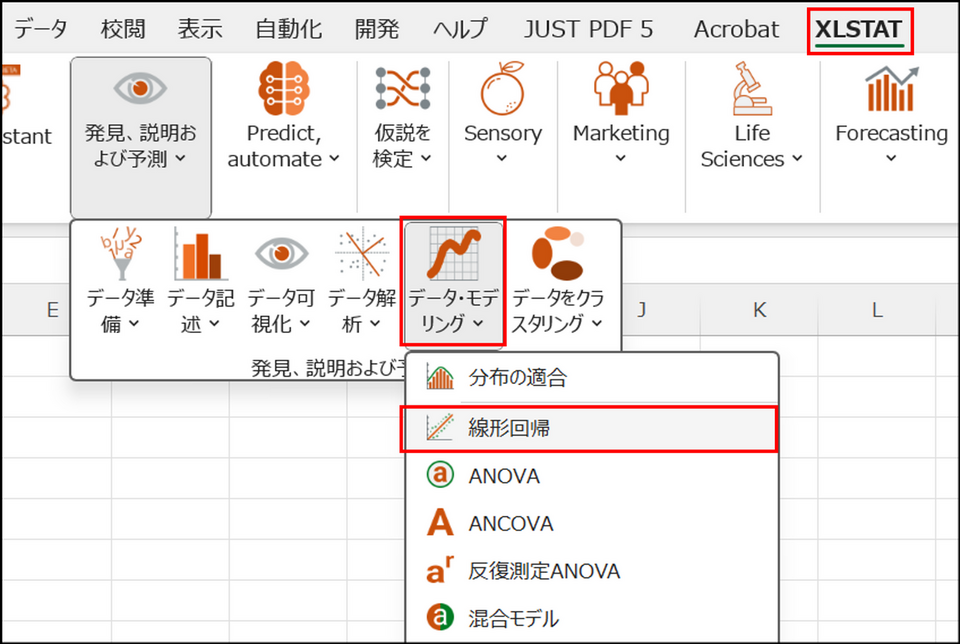
1. XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [線形回帰] を選択します。

   

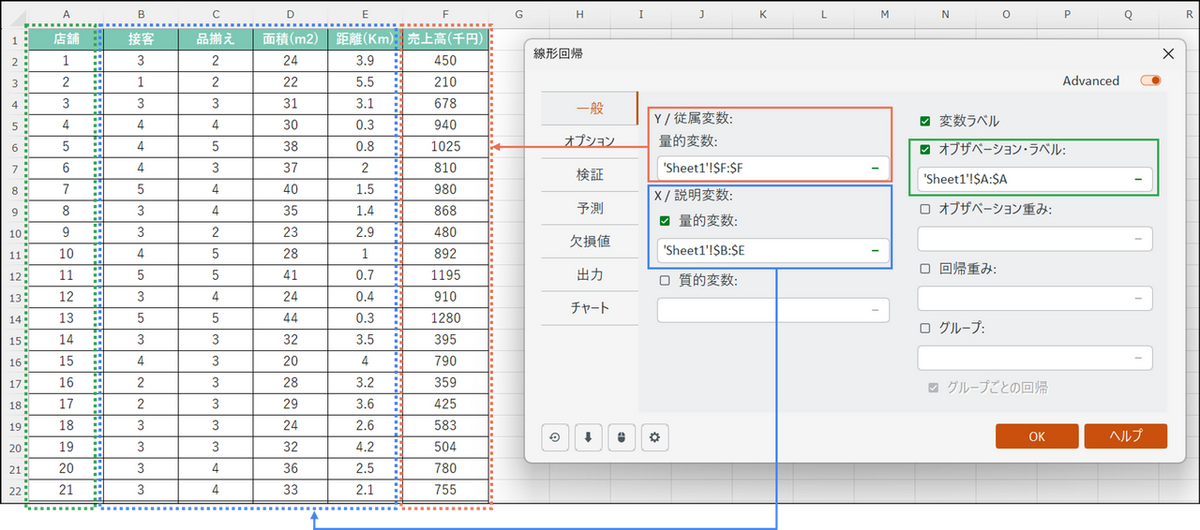
2. ダイアログボックスが開いたら、[一般] タブで以下の設定を行います。

   

   • 従属変数：
     予測したい変数。今回は「売上高」のデータ列を選択します。
     
     
   • 説明変数：
     [量的変数] にチェックを入れ、説明変数である「接客」「品揃え」「面積」「距離」の4つのデータ列をまとめて選択します。
     
     
   • オブザベーション・ラベル（任意）：
     今回はチェックを入れ、「店舗」列を選択します。

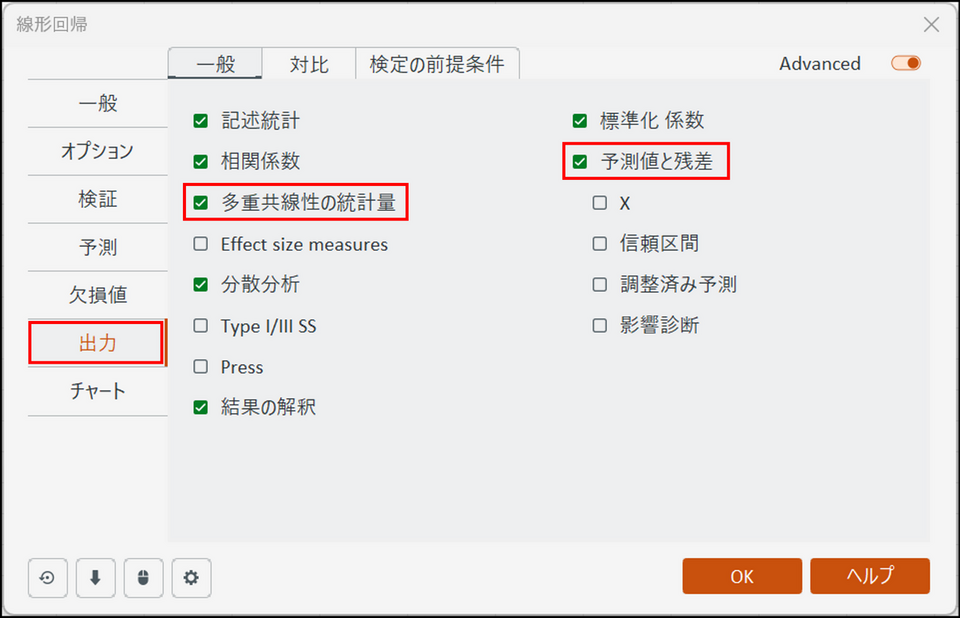
3. [出力] タブに切り替え、[多重共線性の統計量] と [予測値と残差] の項目にチェックを入れます。

   

4. [OK] ボタンをクリックすると、計算が始まり、結果が別シート（線形回帰）に出力されます。

重回帰分析の結果の解釈

出力された結果の中から、特に重要な6つのポイントを見ていきましょう。

1. モデル全体の精度（決定係数と補正R2）

まず、作成された予測モデルが、実際のデータをどの程度うまく説明できているかを確認します。「適合度統計」の表にある R2（決定係数） と 調整済みR2乗（補正R2） を見ます。

• R2（決定係数） ＝ 0.932
• 調整済みR2乗（補正R2）＝0.926

R2（決定係数） は、売上高のばらつきの93.2% を、このモデルで説明できていることを意味します。値は1に近いほど精度が高く、一見すると非常に良いモデルに見えます。しかし、決定係数には「説明変数の数を増やすほど、たとえ意味のない変数を加えても数値が大きくなってしまう」という性質があります。そこで確認するのが調整済みR2乗（補正R2）です。これは、変数を追加することでR2 が大きくなる傾向を踏まえて、説明変数の数に応じて調整された指標です。今回の結果では、補正R2（0.926）は決定係数（0.932）と比べてほとんど低下していません。これは、モデルに採用された4つの変数が、モデルの精度をいたずらに水増しするような不要な変数ではなく、意味のある変数であることを示唆しています。0.926 という値自体も非常に高いため、このモデルは信頼性が高く、非常に優れた予測精度を持つと判断できます。

2. モデル全体の信頼性（分散分析表）

次に、作成した予測モデルが全体として意味のあるものなのか、それとも偶然の結果なのかを統計的に判断します。ここで見るのが「分散分析表」です。この表は、統計的な仮説検定を行っています。まず、「帰無仮説：このモデルは全く役に立たない（すべての係数が0である）」という仮説を立てます。そして、その仮説が正しいとした場合に、手元のデータ（か、それ以上に極端なデータ）が得られる確率を計算します。それがp値（有意確率）であり、今回の結果では「Pr > F」 がそれに該当します。

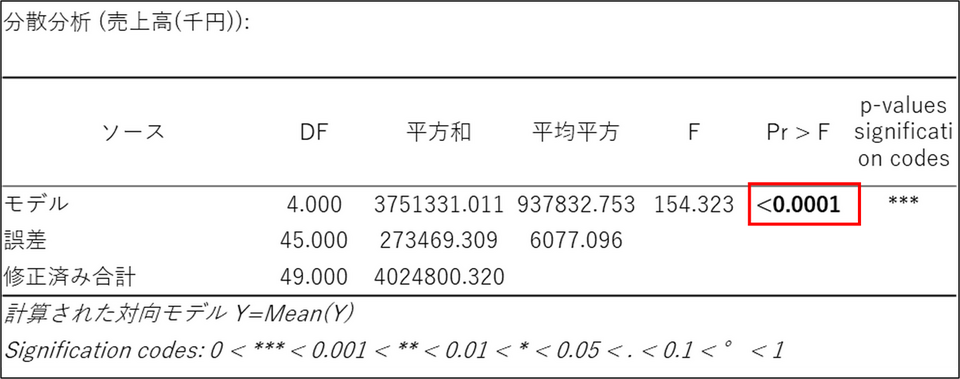
p値は「偶然、このような結果が起こる確率」とイメージすると分かりやすいです。判断の基準として、一般的に有意水準と呼ばれる0.05（5%）が用いられます。

• p値 < 0.05 の場合：
  偶然とは考えにくい（5%未満の確率でしか起こらない）ため、「帰無仮説」を棄却します。
  → モデルは統計的に有意（意味がある）と結論付けます。
  
  
• p値 ≥ 0.05 の場合：
  偶然の範囲内（5%以上の確率で起こりうる）であるため、「帰無仮説」を棄却できません。
  → モデルが有意であるとは言えないと判断します。

今回のp値は「0.0001 未満」であり、基準の0.05 よりはるかに小さい値です。したがって、「このモデルは全く役に立たない」という仮説は棄却され、作成された予測モデルは統計的に非常に信頼性が高いと結論付けることができます。

3. 各要因の影響度と予測モデル式

3-1. 各要因の影響度（モデル・パラメータ）

モデル全体が信頼できることがわかったので、次に個々の説明変数がそれぞれどの程度、売上に影響を与えているかを詳しく見ていきます。そのための表が「モデル・パラメータ」です。

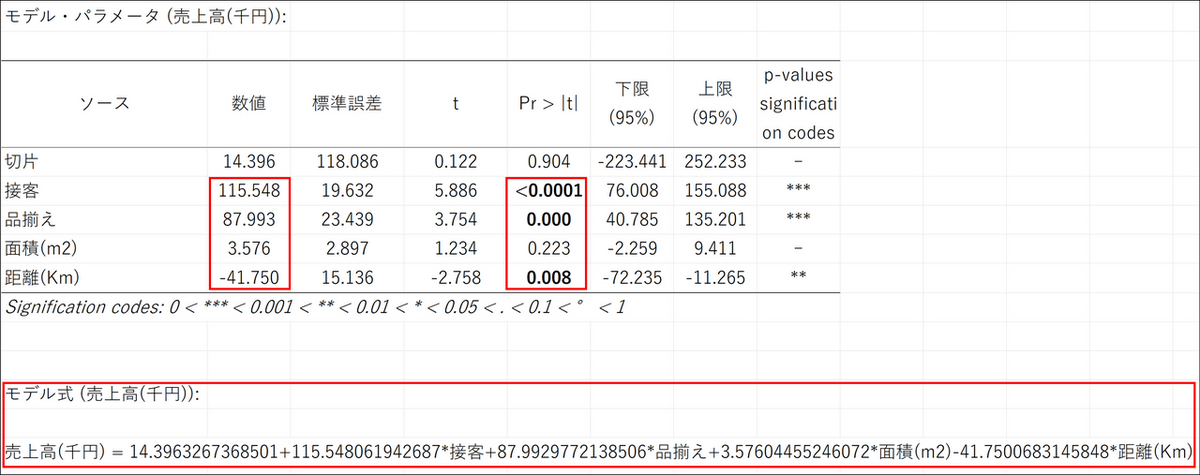
この表で特に重要なのは「数値（係数）」と「p値」です。

• 係数
  ほかの変数がすべて一定であると仮定した場合に、その説明変数が1単位増加すると、目的変数（売上高）がどれだけ増減するかを示します。プラスなら増加、マイナスなら減少を意味します。
  
  
• p値 (Pr > |t|) 
  「その係数は、統計的に意味があると言えるか」を判断するための指標です。ここでも、帰無仮説「この変数の係数は0である（＝売上に影響を与えていない）」を検定しています。p値が0.05未満であれば、その変数は売上に対して統計的に有意な影響を与えていると判断します。

したがって今回の結果は以下のように解釈することができます。

• 接客：
  係数は+115.5、p値は0.0001 未満です。これは「接客スコアが1点上がると、売上が11.5万円増加する」という関係が、統計的に極めて有意であることを示しています。
  
  
• 品揃え：
  係数は+88.0、p値は0.0004 です。同様に、「品揃えスコアが1点上がると、売上が8.8万円増加する」という関係も極めて有意です。
  
  
• 距離(Km)：
  係数は-41.8、p値は0.008 です。マイナスの係数は逆の効果を示し、「駅から1km遠くなるごとに、売上は4.2万円減少する」という関係が有意であることを示しています。
  
  
• 面積(m2)：
  係数は+3.58ですが、p値は0.223 です。これは判断基準の0.05を上回っているため、「面積が売上に与える影響は、統計的に有意であるとは言えない」と結論付けます。つまり、このデータからは、面積を広げることが売上増に繋がるという明確な証拠は見つからなかった、ということになります。

3-2. 予測モデル式（回帰式）の活用

これらの係数を組み合わせたものが、具体的な売上予測を可能にする予測モデル式（回帰式）です。

売上高(千円) = 14.4 + (115.5 × 接客) + (88.0 × 品揃え) + (3.6 × 面積) + (-41.8 × 距離)

この式に具体的な数値を代入することで、まだ存在しない店舗の売上を予測することができます。例えば、以下のような特徴を持つ新規店舗を計画しているとします。

• 接客： 4点（目標値）
• 品揃え： 5点（目標値）
• 面積： 30 m²
• 距離： 0.5 Km

この数値をモデル式に代入してみましょう。

予測売上高 = 14.4 + (115.5 × 4) + (88.0 × 5) + (3.6 × 30) + (-41.8 × 0.5) = 14.4 + 462 + 440 + 108 - 20.9 =1003.5（千円）

この結果から、「この立地とサービスレベルで出店すれば、1日約100万円の売上高が見込める」と、データに基づいた具体的な売上予測が可能になります。これにより、出店判断や事業計画の精度を大きく向上させることができます。

4. 要因の重要度を比較する（標準化係数）

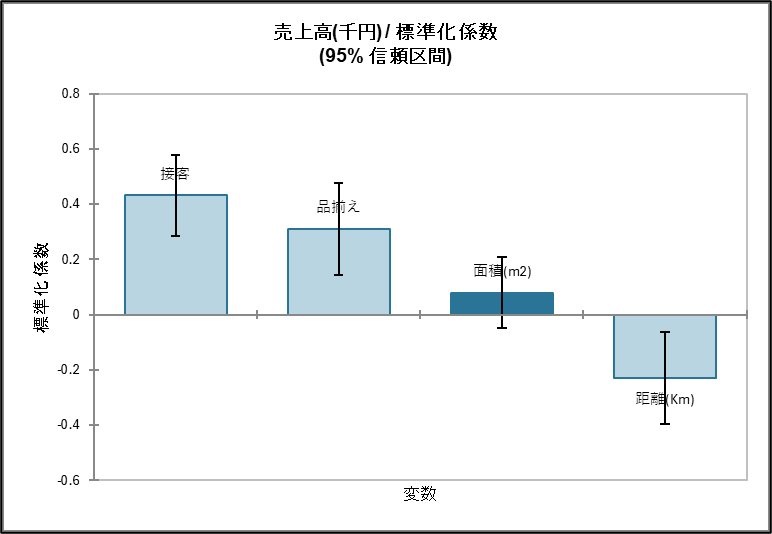
変数の単位が異なるため、影響力の大きさを公平に比較するには標準化係数を見ます。

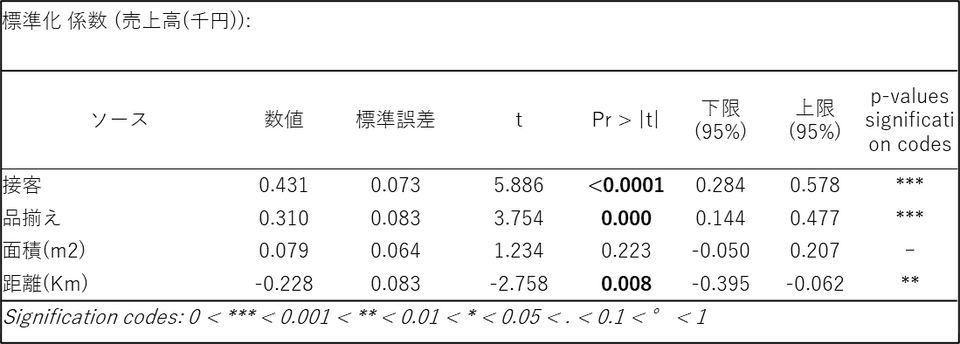
この係数の絶対値が大きい順に、接客 > 品揃え > 距離 > 面積 となり、売上に対して最も影響力が大きいのは「接客」であることが明確にわかります。

5. 多重共線性のチェック

重回帰分析では、分析結果の信頼性を担保するために多重共線性（マルチコリニアリティ。略称マルチコ）をチェックします。多重共線性とはモデルに投入した説明変数同士の相関が強すぎる状態のことです。例えば、アパートの家賃を予測する際に、説明変数として「駅からの距離（km）」と「駅からの徒歩所要時間（分）」の両方を入れてしまうケースが典型です。

この2つの変数は、表現の仕方が違うだけで実質的に同じ情報（駅からどれだけ離れているか）を示しています。このように、同じような意味を持つ変数が複数モデルに含まれていると、家賃への影響が「距離」によるものなのか「時間」によるものなのか、モデルが正しく判断できなくなります。その結果、各変数が与える純粋な影響（係数）が不安定になり、本来プラスになるべき影響がマイナスと算出されるなど、結果を著しく歪める原因となります。多重共線性の程度は「多重共線性の統計量」の表内の許容度と VIF（Variance Inflation Factor: 分散拡大要因）という2つの指標で確認します。なお、これらは互いに逆数の関係（許容度 = 1 ÷ VIF）にあります。

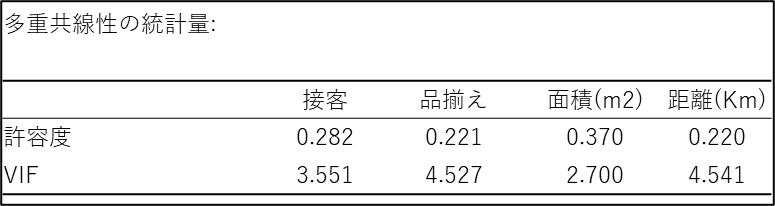
• 許容度：
  ある説明変数のうち、ほかの説明変数では説明できない独立した部分の割合を示します。値が小さいほど、他の変数との重複が大きく、多重共線性の疑いが強まります。通常、許容度の値が0.1 以下のときに多重共線性が生じていると判断されます。
  
  
• VIF：
  許容度の逆数（VIF＝1÷許容度）で、値が10以上であると多重共線性が発生していると判断されます。VIF＝10 は相関係数に換算するとおよそ0.95 という、かなり高い値に相当します。このような強い相関を持つ変数を両方とも回帰モデルに含めてしまうと、モデルの解釈が困難になるため避けるべきです。ただし、「VIF が10 以上」という基準はあくまで一つの目安であり、多重共線性の強さはサンプルサイズによっても変わるため、絶対的なものではありません。

もし分析の結果、強い多重共線性があることが判明した場合には、対処法として関連性の高い変数を削除したり、統合したりといった見直しを検討する必要があります。今回の分析ではVIF の最大値は 4.541 で10未満であり、許容度も危険水域である「0.1」を上回っているので、多重共線性の問題はなく、この分析結果は信頼できると判断できます。

6. モデルの予測精度を個別に確認する（予測値と残差）

「予測値と残差」の表では、モデルが各店舗の売上をどれだけ正確に予測できたかを個別に確認できます。

• 予測値：作成された予測モデルが算出した売上高。
  
  
• 残差：「実際の売上高」 - 「予測値」。予測がどれだけズレていたかを示します。
  
  
• 標準化残差： 残差を標準化した値。絶対値が2（より厳密には1.96）を超える場合、予測が大きく外れた「外れ値」と判断できます。

例えば、標準化残差が-2.544 となっている店舗は、モデルの予測を大幅に下回る売上しかなく、「何か特別な要因があるのではないか？」とさらに深掘りして調査するきっかけになります。

まとめ

今回の分析から、店舗売上には「接客」と「品揃え」が最も重要なプラス要因であり、「駅からの距離」がマイナス要因として強く影響していることが明らかになりました。この結果は、今後の店舗運営戦略において、人材教育や商品構成、新規出店計画などに具体的な示唆を与えてくれます。このように、結果に対する要因の切り分けや、将来の予測を行いたい場合に重回帰分析は欠かせないツールとなります。そして、XLSTAT を活用することで、こうした高度な分析を使い慣れたエクセル上でシームレスに実行できます。専門的なプログラミング知識は不要で、直感的な操作だけで、ビジネスの意思決定に必要な情報を網羅的に得ることが可能です。ぜひXLSTAT を使って、課題解決や新たな戦略立案のために重回帰分析をご活用ください。

参考文献

• XLSTAT: Multiple Linear Regression in Excel
  https://community.lumivero.com/s/article/6685-multiple-linear-regression-excel-tutorial?language=en_US

• 阿部真人: データ分析に必須の知識・考え方　統計学入門　仮説検定から統計モデリングまで重要トピックを完全網羅, ソシム, 2021.

• いちばんやさしい、医療統計. R で多重共線性をチェックするために VIF を計算する方法
  https://best-biostatistics.com/toukei-er/entry/how-to-calculate-vif-by-r/

• 末吉正成, 末吉美喜: EXCELビジネス統計分析[ビジテク] 第3版, 翔泳社, 2017.

• 豊田 裕貴: Excelで学ぶ 実践ビジネスデータ分析, オデッセイ コミュニケーションズ, 2023.

• 平井明代：教育・心理系研究のためのデータ分析入門 第2版―理論と実践から学ぶSPSS 活用法, 東京図書, 2022.

XLSTAT の無料トライアル

トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した重回帰分析析はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。