• ROC 曲線とは？
• ROC 曲線で使われる用語と説明
• ROC 曲線を作成するためのデータセット
• XLSTAT でROC 曲線を作成する手順
• ROC 曲線の出力結果の解釈
• ROC 曲線の比較（応用）
• まとめ
• 参考文献
• XLSTAT の無料トライアル

ROC 曲線とは？

ROC 曲線とは、「YES かNO か」や「AかBか」といった2つの結果に分類するテストや予測モデルの性能を評価するためのグラフです。医療統計においては、ある病気の検査が「陽性（Positive）」と「陰性（Negative）」をどれだけ正しく識別できるのかを評価する際に用いられます。一言でいうと、「検査やテストの性能を評価するための成績表」のようなものです。

例えば、新しい病気の検査方法を開発したとします。この検査がどれくらい優秀かを評価するには、以下2つの能力が重要です。

• 病気を見逃さない能力（感度）：
  本当に病気の人を、正しく「陽性（病気である）」と判断する能力（真陽性率）。
  
  

• 病気ではない人を正しく見分ける能力（特異度）：
  健康な人を正しく「陰性（病気ではない）」と判断する能力（真陰性率）。

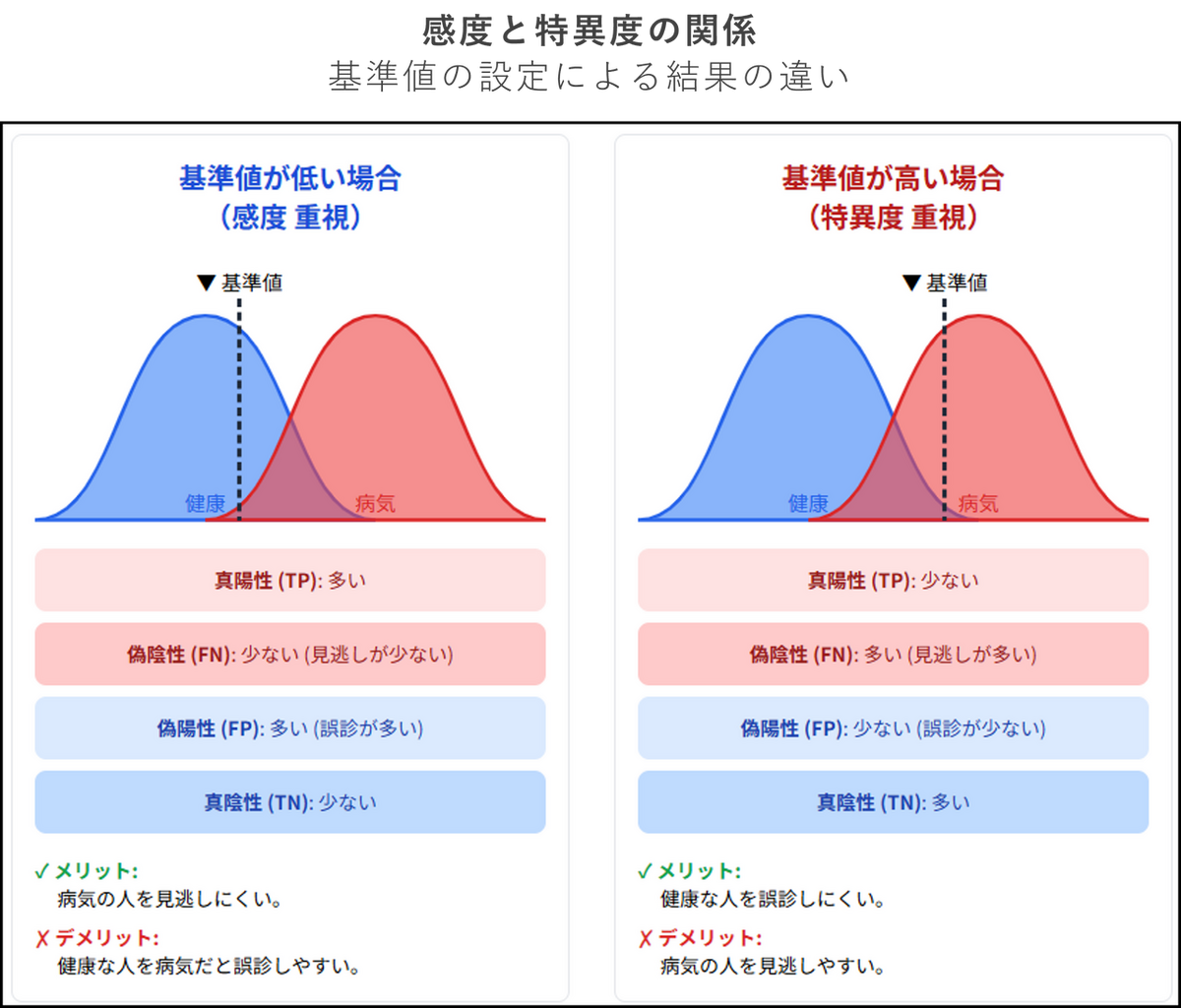
通常、検査においてはある値が基準値（閾値）を超えていれば「陽性」かどうかを判断します。このときの基準値（閾値）を低く設定すれば、「病気を見逃さない能力（感度）」は上がりますが、健康な人まで「陽性（病気である）」と判断してしまう間違い（偽陽性）が増えます。反対に基準値を高く設定すると、病気の人まで「陰性（病気でない）」と判断してしまうリスクが増えてしまいます。このように「感度」と「特異度」はトレードオフの関係にあります。

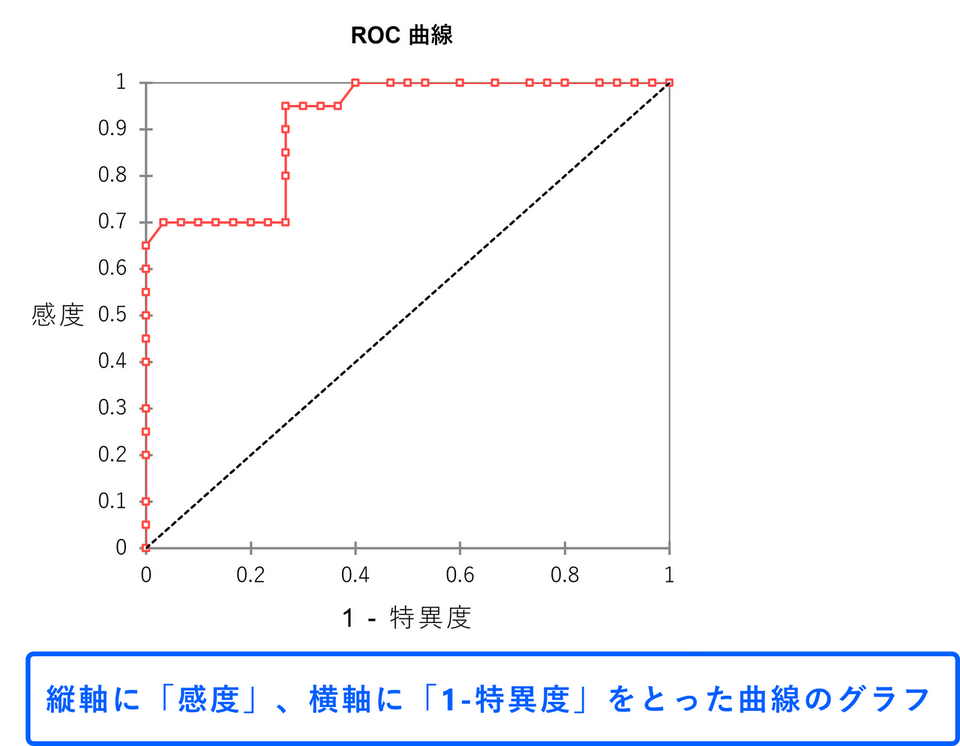
ROC 曲線は、このトレードオフの関係性を示しており、縦軸に感度、横軸に偽陽性率（1 - 特異度）をとって作成されます。閾値を連続的に変化させたときの、感度と偽陽性率のペアをプロットして一本の曲線が描かれているので、「感度をこれだけ上げると、特異度はこれだけ下がる」という具体的なバランスを見ながら、最適な基準値を判断するのに役立ちます。

ROC 曲線で使われる用語と説明

ROC 曲線を理解するために、まずは基本的な4つの分類と、そこから計算される主要な指標を理解しておきましょう。

結果の基本4分類（混同行列）

どんな検査も、実際の結果と照らし合わせると、以下の4パターンに分けられます。

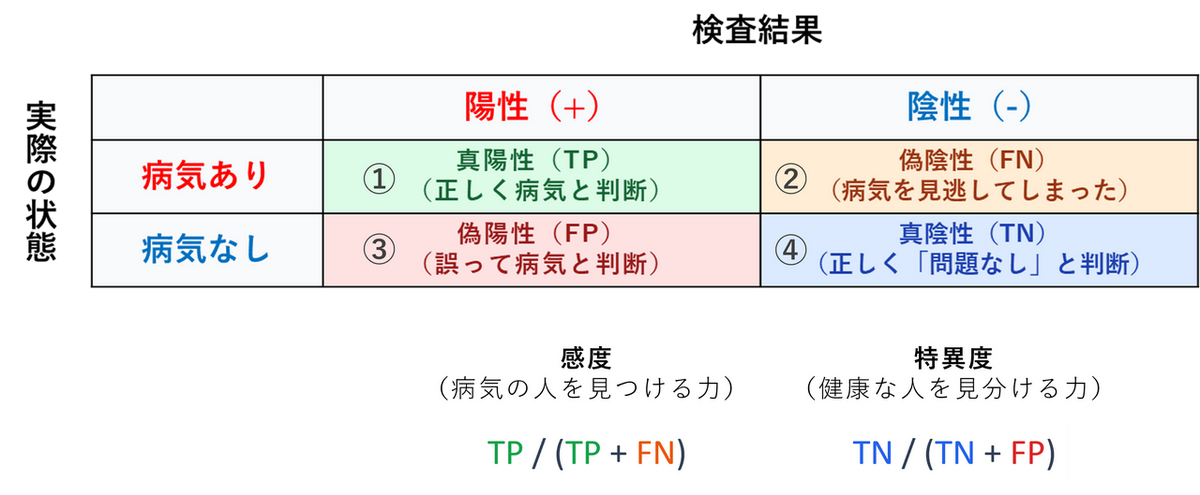
主要な評価指標

• 感度（Sensitivity）
  本当に病気の人のうち、検査で正しく「陽性」と判定された人の割合。病気の見逃しにくさを示します。計算式：感度＝TP / (TP + FN)。

• 特異度（Specificity）
  本当に健康な人のうち、検査で正しく「陰性」と判定された人の割合。健康な人を間違って病気と診断しない正確さを示します。計算式：特異度＝TN / (TN + FP)。

• 偽陽性率（False Positive Rate; FPR）
  健康な人のうち、間違って「陽性」と判定された人の割合。ROC 曲線の横軸に使われます。計算式: 偽陽性率＝1−特異度＝FP / (FP+TN)。

• 陽性的中率 （Positive Predictive Value; PPV）
  検査で「陽性」と判定された人の中で、本当に病気だった人の割合。

• 陰性的中率（Negative Predictive Value; NPV）
  検査で「陰性」と判定された人の中で、本当に健康だった人の割合。

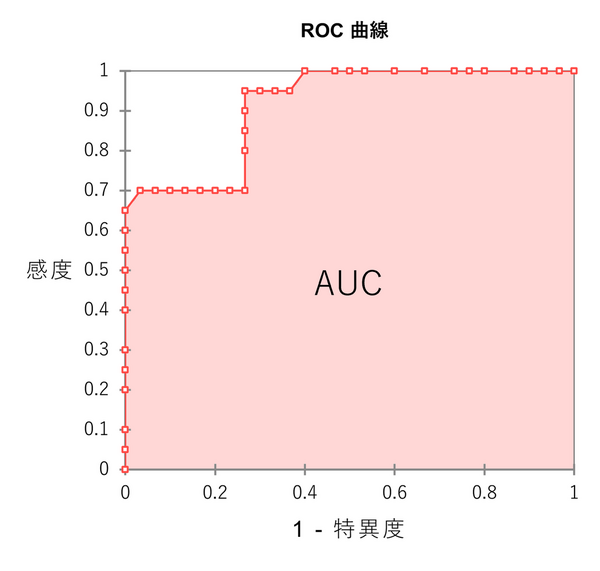
• AUC（Area Under the Curve）
  ROC 曲線と底辺で囲まれた部分の面積で、検査全体の総合的な性能を示す0 から1 の間の数値です。1に近いほど高性能です。
  • AUC = 1：完璧な検査
  • AUC > 0.9：非常に優秀な検査
  • 0.7 < AUC < 0.9：まあまあ良い検査
  • AUC = 0.5：当てずっぽうと同じレベル（役に立たない）

• カットオフ値（Cut-off Value） / 閾値（Threshold）
  検査結果のような連続的な数値を、「陽性」か「陰性」か、あるいは「A」か「B」かという2つのカテゴリに分類するための境界となる値のことです。例えば、「テストの点数が70点以上なら合格」という場合の「70点」がカットオフ値にあたります。この値をどこに設定するかで、感度と特異度のバランスが大きく変わるため、ROC 分析において最も重要な要素の一つです。

ROC 曲線を作成するためのデータセット

今回は、50名に対して実施したあるウイルス検査の結果を記録したデータを使用します。

データセットには以下2つの情報が記録されています。

• 疾患の有無：
  実際にウイルスに感染しているかどうかの情報（20人が「あり」、30人が「なし」）。感染している場合は「+」、感染していない場合は「-」で表記しています。
  
  
• 濃度：
  新しい検査で測定した血中のウイルス濃度。

今回はこのデータを用いて、ROC 曲線を作成し、検査結果の濃度がどのくらいの値であれば、患者が「病気である」と見なせるかを判断したいと思います。

サンプルデータのダウンロードはこちらから

Sample-Dataset-for-ROC.xlsm

XLSTAT でROC 曲線を作成する手順

1. XLSTAT を起動し、[Life Sciences] > [生存期間分析] > [ROC 曲線] を選択します。

   

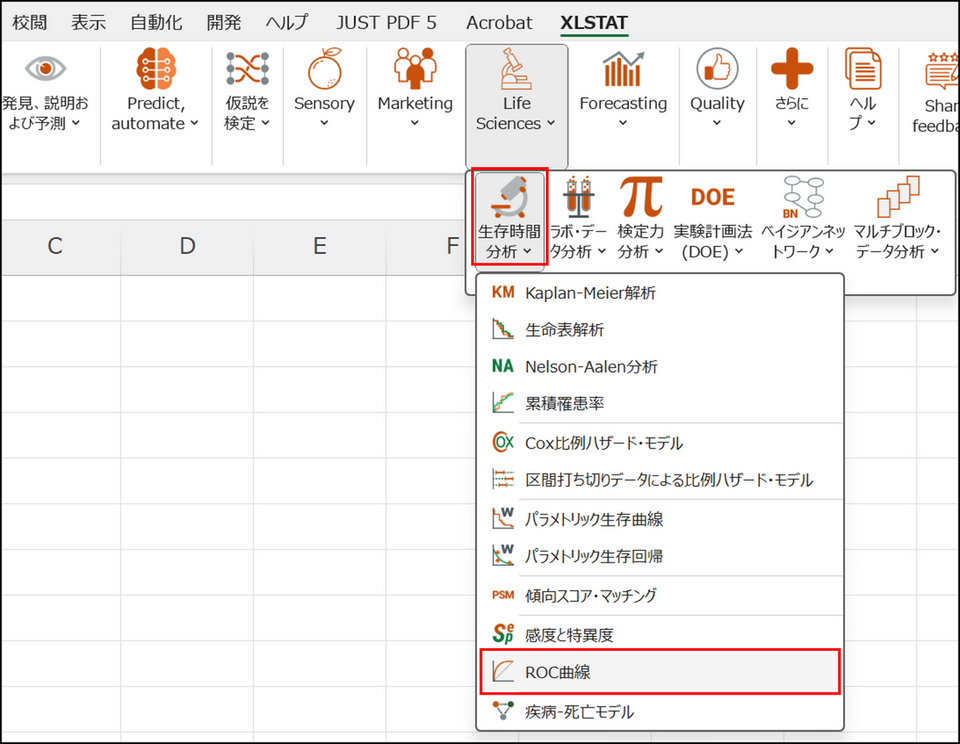
2. ダイアログボックスが開いたら、[一般] タブで以下の設定を行います。

   

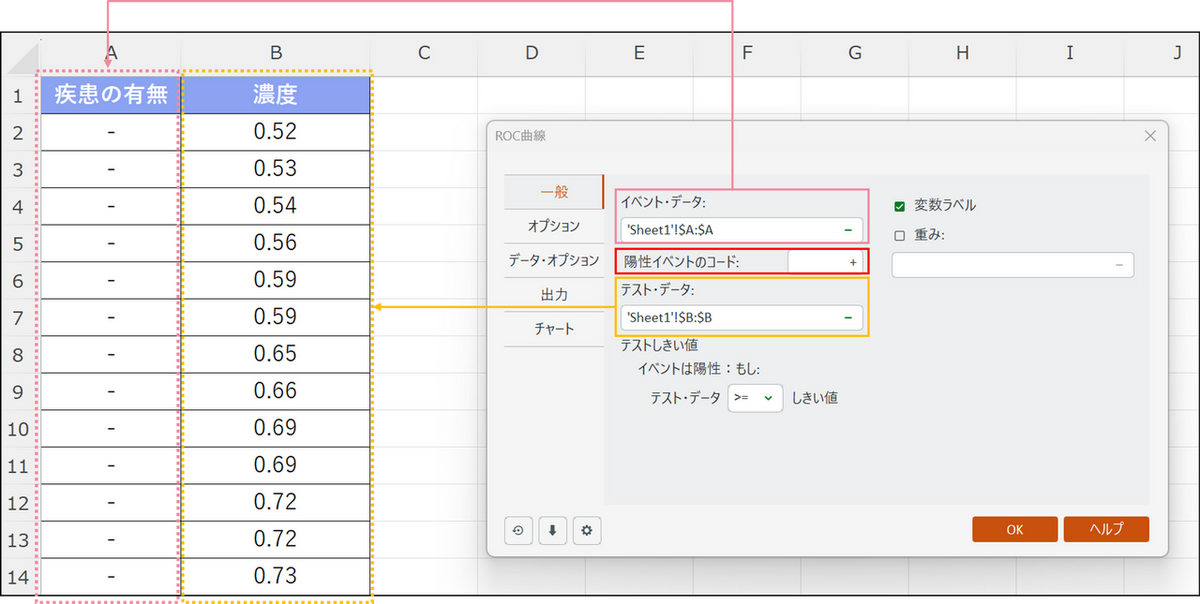
   • イベントデータ：
     「疾患の有無」のデータが入力されている列を選択します。
     
     
   • 陽性イベントのコード：
     陽性を示すコード（今回のデータでは「+」）を入力します。
     
     
   • テスト・データ：
     検査結果の数値である「濃度」のデータ列を選択します。
     
     
   • テストしきい値：
     今回は「濃度が高いほど陽性らしい」と考えるので、「>=（以上）」を選択します。

3. [オプション] タブに切り替え、以下のように設定します。

   

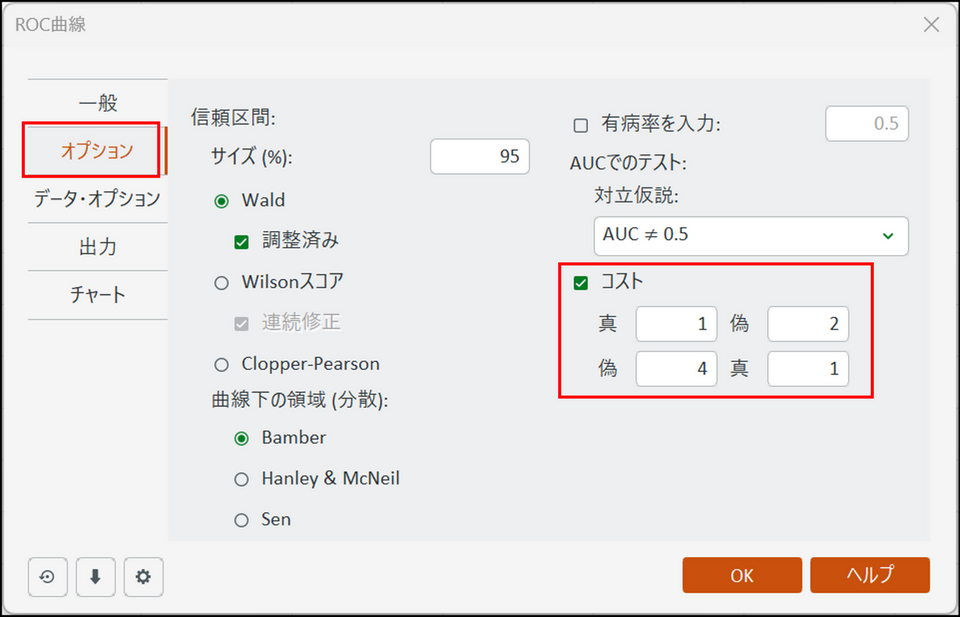
   • 信頼区間：
     各指標の信頼区間の範囲（通常は95%）や計算方法を選択できます。

   ---

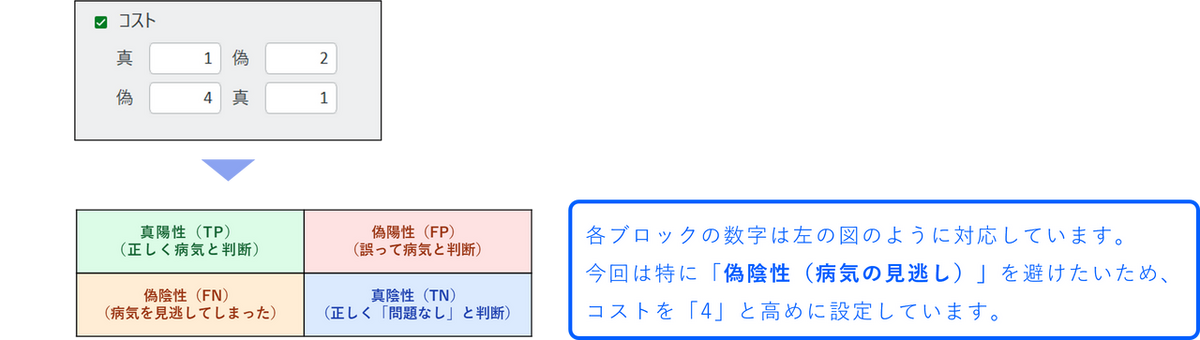
   • コスト：
     偽陽性（FP）や偽陰性（FN）といった診断ミスの「重大さ（コスト）」を設定できます。特に「病気を見逃す（FN）」コストを重く設定すると、より安全な基準値を見つけやすくなります。

   ---

   

4. [出力] タブに切り替え、以下のように設定します。

   

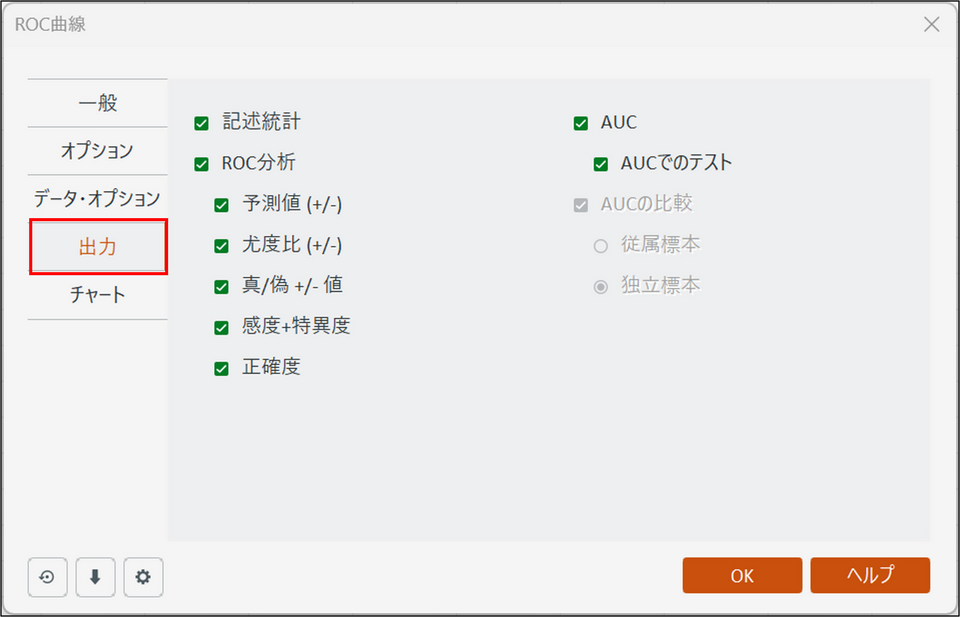
5. [チャート] タブに切り替え、以下のように設定します。

   

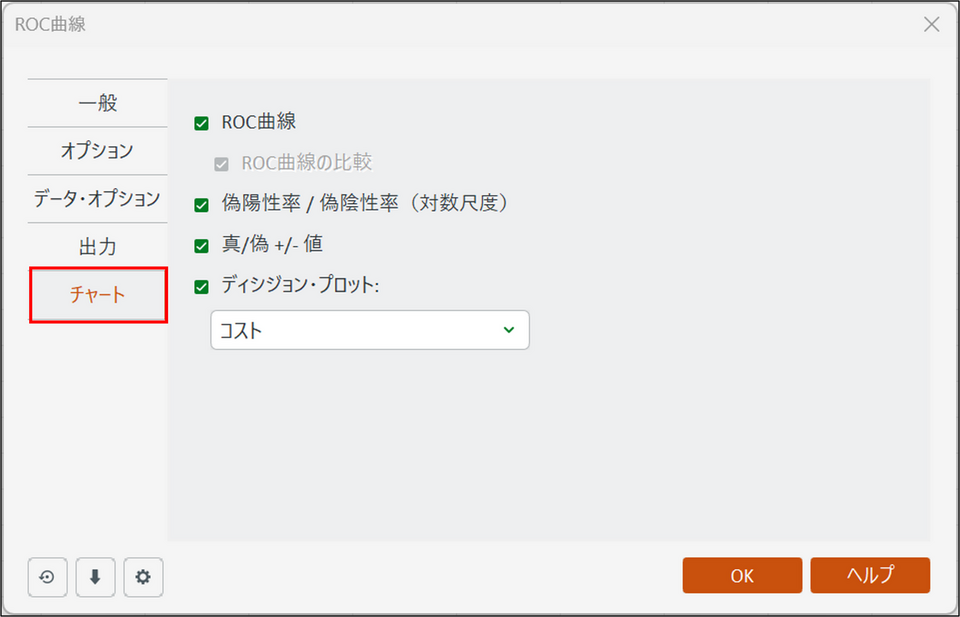
6. [OK] ボタンをクリックすると、計算が始まり、結果が別シート（ROC曲線）に出力されます。

ROC 曲線の出力結果の解釈

記述統計

最初の表では、テスト変数（この例では「濃度」）の記述統計量が表示され、続いてイベント変数（この例では「疾患の有無」）の統計量が表示されます。今回のデータで観測された有病率は0.4 です。

ROC 曲線（グラフ）

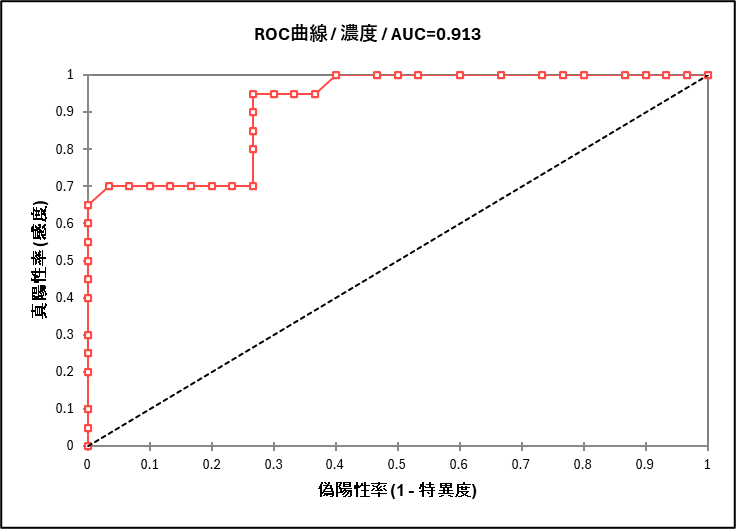
ROC 曲線は、以下2つの軸で構成されています。

• 縦軸（Y軸）: 感度（真陽性率）
• 横軸（X軸）: 偽陽性率（1 - 特異度）

まずは曲線の形に着目します。曲線がグラフの左上に向かって大きく膨らんでいるほど、検査性能が高いことを示しています。一方で、グラフの中央を斜めに走る点線は、「当てずっぽう」な予測を表します。曲線がこの点線から上側に離れているほど、意味のある検査だと言えます。次にAUC の値を見て、検査の総合評価を行います。AUC は最大1 で、1 に近いほど高性能です。今回のデータではAUC が「0.913」なので、非常に優れた検査であると判断できます。さらに結果の末尾に表示される「AUC=0.5との比較」の検定結果でも、p 値が十分に小さいので（例：p < 0.05）、検査が統計的に「当てずっぽうよりは優れている」ことが証明されています。

ROC分析（表）

「濃度」の値を変更していった場合に、感度や特異度などの各指標がどのように変化するかが一覧になっています。この表を見ることで、例えば「感度を80%以上に保つには、基準値をどこに置けばよいか」といった具体的な検討ができます。また、間違いによる損失（コスト）が最も少なくなると判断された基準値の行は太字で示されます。これにより、検査のカットオフ値をどこに設定すれば良いのかを判断できます。今回のデータではカットオフ値を「0.98」にするのが良さそうです。

ROC分析（表）の下には、上記表を使用して作成されたグラフが表示されます。閾値に応じて、TP（真陽性）、TN（真陰性）、FP（偽陽性）、およびFN（偽陰性）の計数の変化を確認することができます。

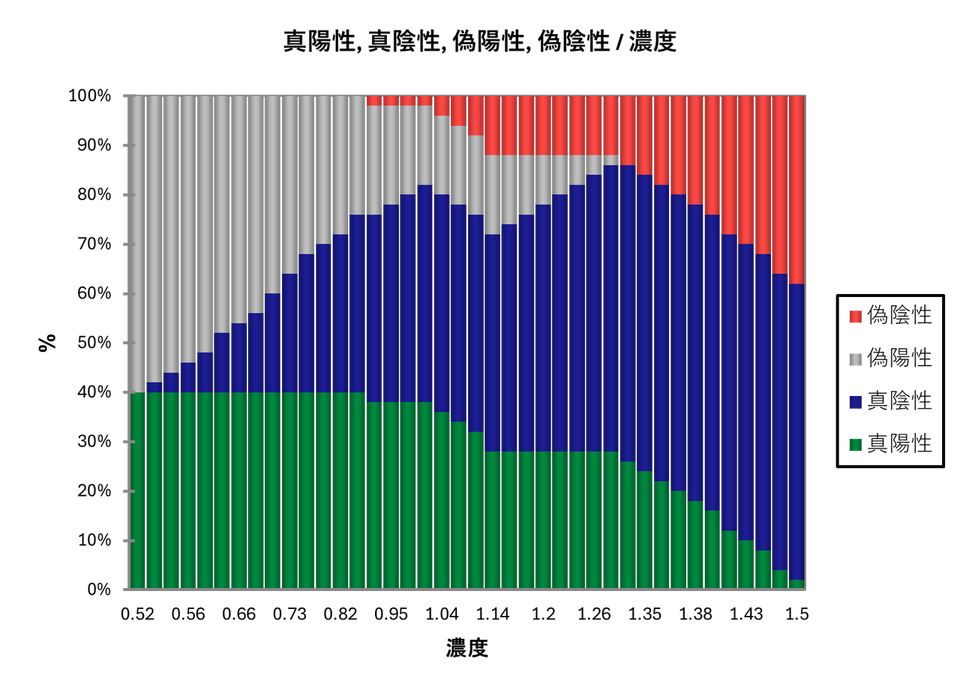
決定プロット（グラフ）

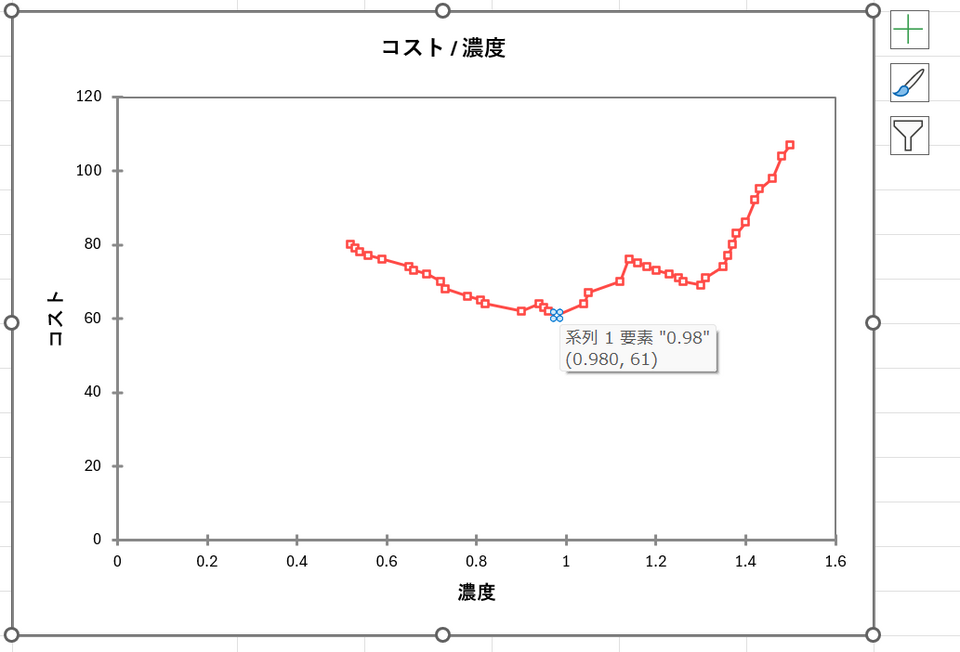
[オプション] タブでコストを設定した場合、このグラフが表示されます。グラフの谷が最も深くなっている点が、設定したコストを最小にする「最適な基準値」を示します。マウスを合わせると、その時の具体的な基準値を確認できます。

ROC 曲線の比較（応用）

もとのデータにグループ列を追加して、2つのROC 曲線を作成・比較することも可能です。

1. [データ・オプション] タブにて、[グループごと分析] の項目にチェックを入れ、グループ列を選択します。

   

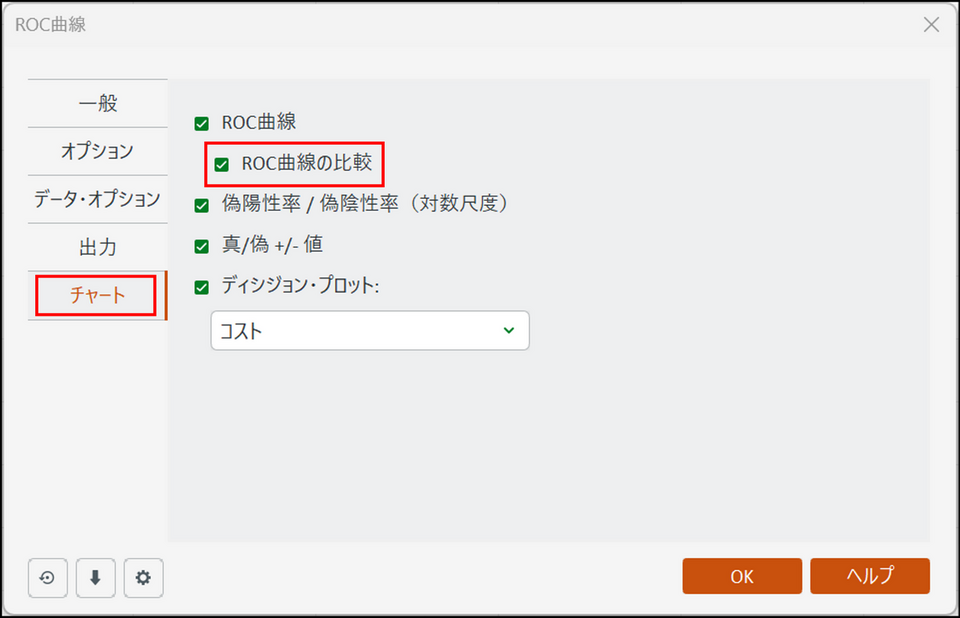
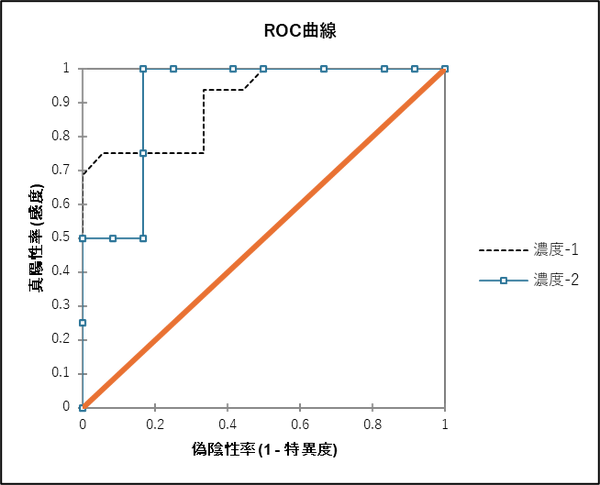
2. [チャート] タブにて、[ROC 曲線の比較] の項目にチェックを入れ、実行します。

   

まとめ

ROC 曲線は、診断テストや分類モデルの性能を客観的かつ視覚的に評価するための非常に便利な手法です。XLSTAT を使えば、複雑な計算も簡単な操作で実行でき、AUC による総合評価から、感度・特異度のバランスを考慮した最適な基準値の探索まで、多角的な分析が可能になります。

参考文献

• Agresti A. (1990). Categorical Data Analysis. John Wiley and Sons, New York.

• Agresti A., and Coull B.A. (1998). Approximate is better than "exact" for interval estimation of binomial proportions. The American Statistician, 52, 119-126.

• Agresti A. and Caffo, B. (2000). Simple and effective confidence intervals for proportions and differences of proportions result from adding two sucesses and two failures. The American Statistician, 54, 280-288.

• Bamber D. (1975). The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. Journal of Mathematical Psychology, 12, 387-415.

• Clopper C.J. and Pearson E.S. (1934). The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika, 26, 404-413.

• DeLong E.R., DeLong D.M., Clarke-Pearson D.L. (1988). Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics, 44(3), 837-845.

• Hanley J.A. and McNeil B.J. (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 143, 29-36.

• Hanley J. A. and McNeil B. J. (1983). A method of comparing the area under two ROC curves derived from the same cases. Radiology, 148, 839-843.

• Newcombe R. G. (1998). Two-sided confidence intervals for the single proportion: comparison of seven methods. Statistics in Medicine, 17, 857-872.

• Pepe M.S. (2003). The Statistical Evaluation of Medical Tests for Classification and Prediction, Oxford University Press.

• Sen P. K. (1960). On some convergence properties of U-statistics. Calcutta Statistical Association Bulletin, 10, 1-18.

• Wilson, E.B. (1927). Probable inference, the law of succession, and statistical inference. Journal of the American Statistical Association, 22, 209-212.

• Wald, A., & Wolfowitz, J. (1939). Confidence limits for continuous distribution functions. The Annals of Mathematical Statistics, 10, 105-118.

• XLSTAT: ROC curve analysis in Excel
  https://community.lumivero.com/s/article/6627-roc-curve-analysis-excel-tutorial?language=en_US
  
  
• XLSTAT: ROC curves comparison in Excel
  https://community.lumivero.com/s/article/6635-roc-curves-comparison-excel-tutorial?language=en_US

• Zhou X.H., Obuchowski N.A., McClish D.K. (2002). Statistical Methods in Diagnostic Medicine. John Wiley & Sons.

XLSTAT の無料トライアル

トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介したROC 曲線はAdvanced のライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。