XLSTAT による一元配置分散分析(ANOVA):3種類以上のチョコレートの味の評価を比較する
- 分散分析(ANOVA)とは?
- 分散分析で使われる用語
- 一元配置分散分析を実行するためのデータセット
- 一元配置分散分析の操作手順
- 一元配置分散分析の結果の解釈
- 多重比較の問題(補足)
- まとめ
- 参考文献
- XLSTAT の無料トライアル
分散分析(ANOVA)とは?
分散分析(ANOVA: Analysis of Variance)は、複数のグループ間で平均値に差があるかどうかを調べる方法です。例えば、異なる講習A、B、C を受講した各生徒のテストの点数を比較し、それぞれの講習によってテストの平均点が異なるかどうかを統計的に判断します。
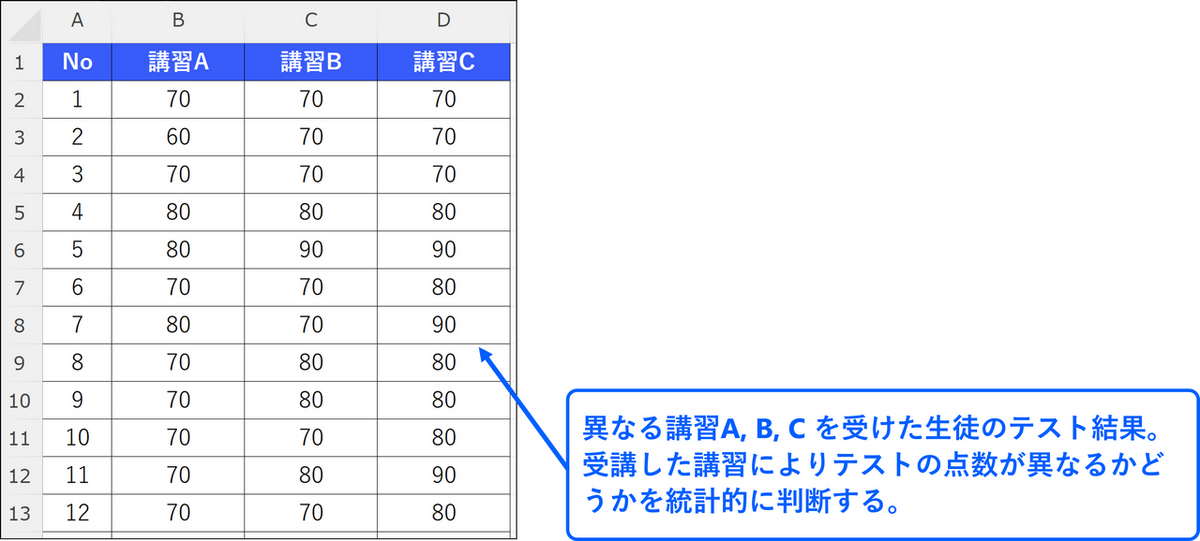

上記の例では講習C を受講した生徒のテストの平均点が一番高いことがわかりましたが、この結果だけで「講習C がテストの点数に一番効果がある」と判断しても問題ないでしょうか。今回取得したデータではたしかに講習C を受講した生徒のテスト結果が一番優れていますが、たまたま良い結果が出ただけという可能性も考えられます。
このように3グループ以上の平均値の差が偶然によるものか、それとも統計的に有意な差なのかという疑問に答えるのが今回ご紹介する「分散分析」です。
分散分析で使われる用語
分散分析では以下の用語が使われます。
- 要因/因子:
結果に影響を与えると考えられる変数です。例えば、ある商品の販売数を比較する調査であれば、「販売地域」や「広告方法」などが要因/因子となります。
※「要因」と「因子」の使い分けは参考文献により異なりますが、結果に影響を与えると考えられる要素を「要因」と通称し、その要因の中で意識的に採り上げたものを「因子」と呼びます。 - 水準:
1つの要因に含まれる項目(グループ)のことです。上記事例の場合は、「講習」の水準は「A、B、C」の3つであり、水準数は「3」となります。
因子の数が1つの場合は一元配置分散分析、因子の数が2つの場合は二元配置分散分析と呼ばれます。
このページではXLSTAT で「一元配置分散分析」を実行する方法をご紹介します。
一元配置分散分析を実行するためのデータセット
このページでは、24名の消費者パネルに、4種類のチョコレート(A, B, C, D)の味を7段階で評価してもらったデータを使用します。このデータでは因子は「チョコレート」で、水準は「A, B, C, D」の4種類になります。
1人が4種類のチョコレートすべてについて評価したデータでは対応がありますが、このデータでは1人が1つのチョコレートについて評価しているため、対応のないデータとなります。
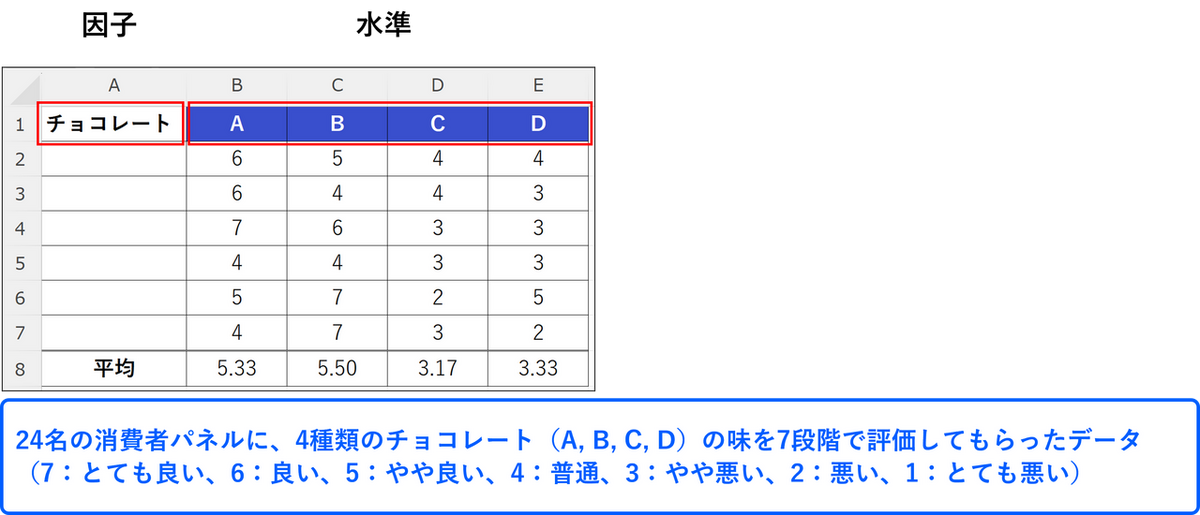
一見すると、A またはB のチョコレートは、C またはD のチョコレートよりも評価が高そうです。しかし、たまたまこのようなデータが得られた可能性も考えられます。今回はXLSTAT で一元配置分散分析を実行し、チョコレートの種類によって味の評価に違いがあるのかを確認してみます。
サンプルデータのダウンロードはこちらから
One-Way-ANOVA-Sample-Data.xlsm一元配置分散分析の操作手順
-
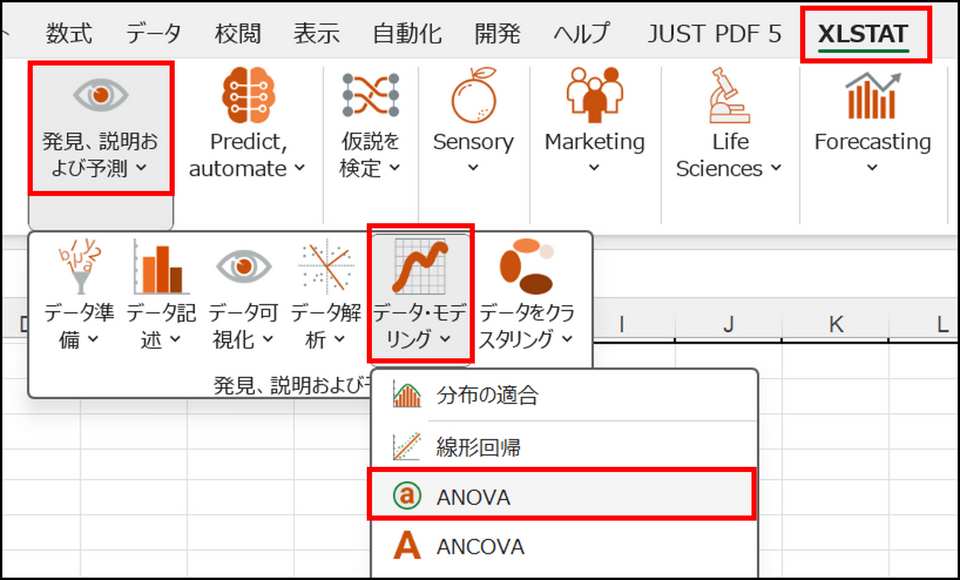
XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [ANOVA] を選択します。
-
ダイアログボックスが表示されるので、下記項目を指定します。
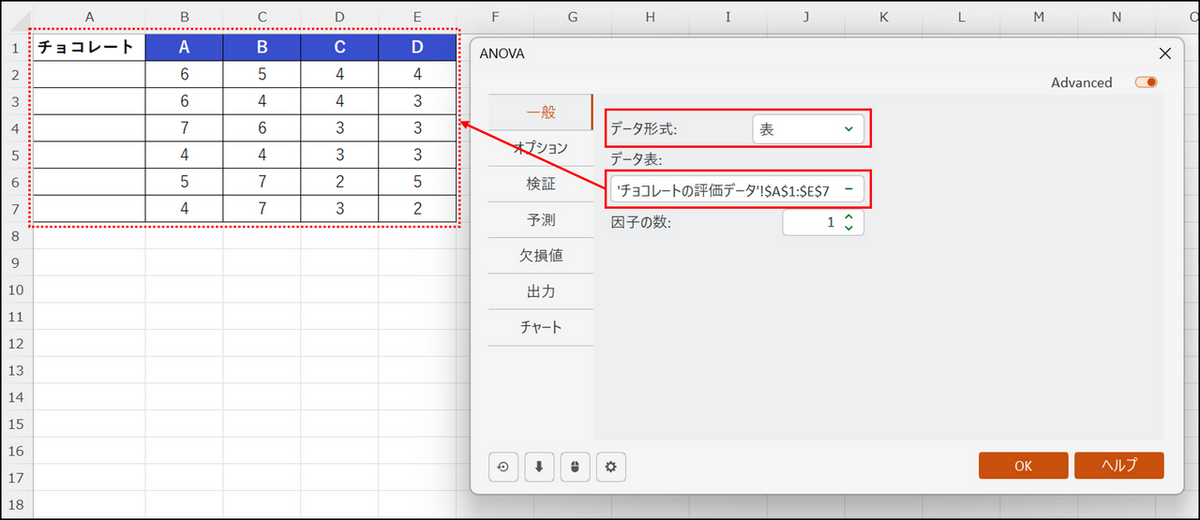
- データ形式:[表] を選択。列形式のデータであれば、[列] を選択します。
- データ表:分析対象のデータセルを直接選択
※A 列の因子(「チョコレート」)も含めて選択します。
【補足】
データ形式が列の場合は、以下のようにデータを選択します。
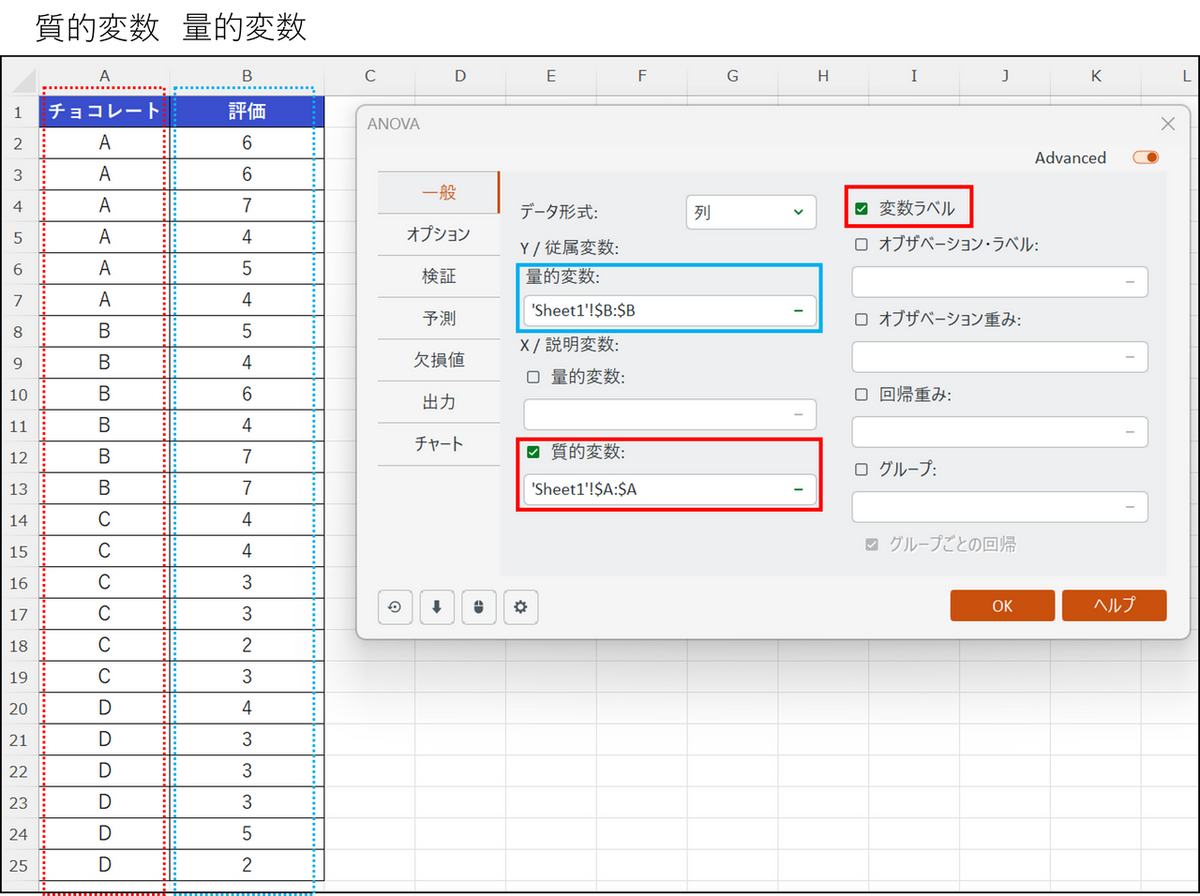
- データ形式:[表] を選択。列形式のデータであれば、[列] を選択します。
-
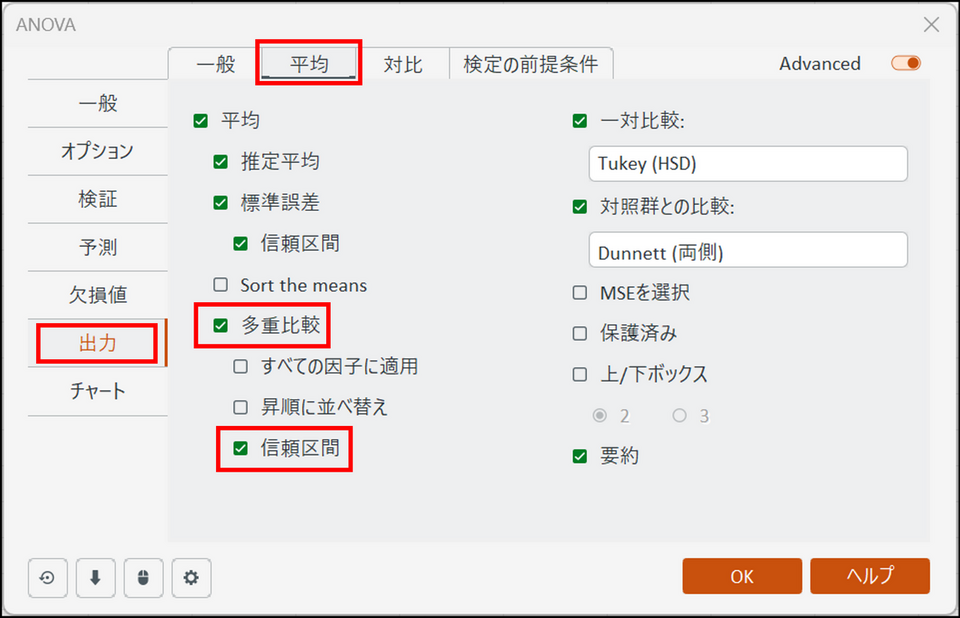
[出力] の[平均] タブに切り替え、[多重比較] と[信頼区間] にチェックを入れます。
-
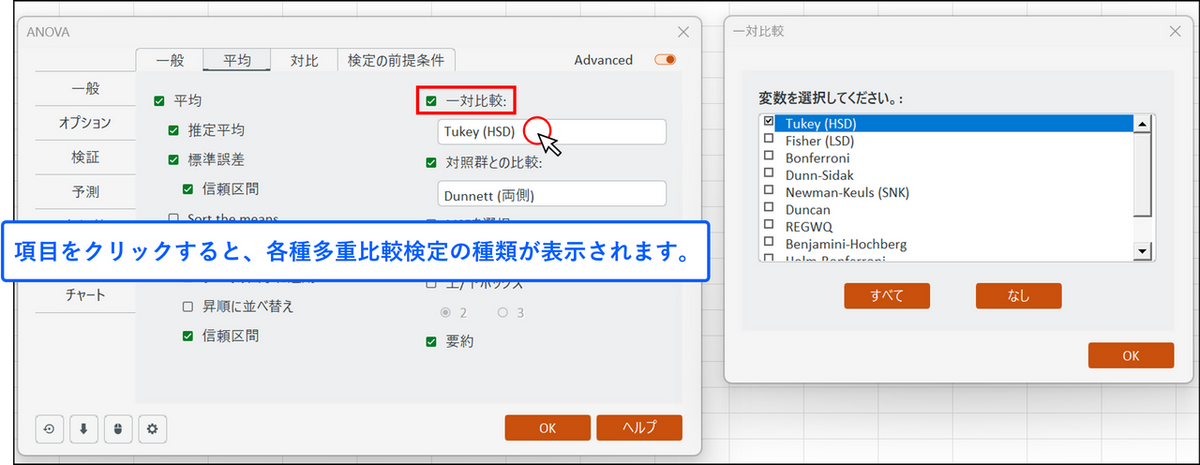
[一対比較] の項目にチェックを入れ、[Tukey (HSD)] を選択します。
-
[対照群との比較] にもチェックを入れ、[Dunnett (両側)] を選択します。

-
[OK] ボタンをクリックします。
-
[コントロール・カテゴリー選択] ダイアログボックスで、[チョコレート-A] を選択し、[OK] をクリックします。
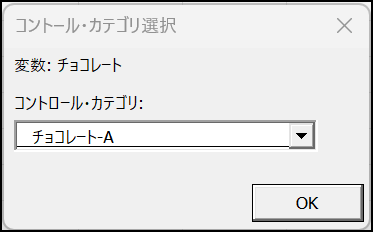
※ダネット検定(Dunnett’s test)では1つの対照群( コントロール群とも呼びます )とそのほかのグループとの比較を行うため、コントロールカテゴリーを選択します。今回はチョコレートA とそのほかのチョコレート(B〜D)を比較したいため、ここではチョコレートA を選択します。
-
計算が実行され、結果が別シート(ANOVA)に出力されます。
一元配置分散分析の結果の解釈
分析結果には、様々な表やグラフが出力されますが、特に重要なのは「分散分析表」と「多重比較検定」の結果です。
分散分析表
分散分析表ではp 値に注目します。今回の場合、p 値は0.001 となっています。つまり、チョコレートにより味の評価がすべて同じという仮定で、今回のデータが偶然得られる可能性は0.1%であることを示しています。5%有意水準を採用するなら、p 値が0.05 よりも小さいため、「今回のデータから、チョコレートにより味の評価が異なる(有意差あり)」と主張できることになります。
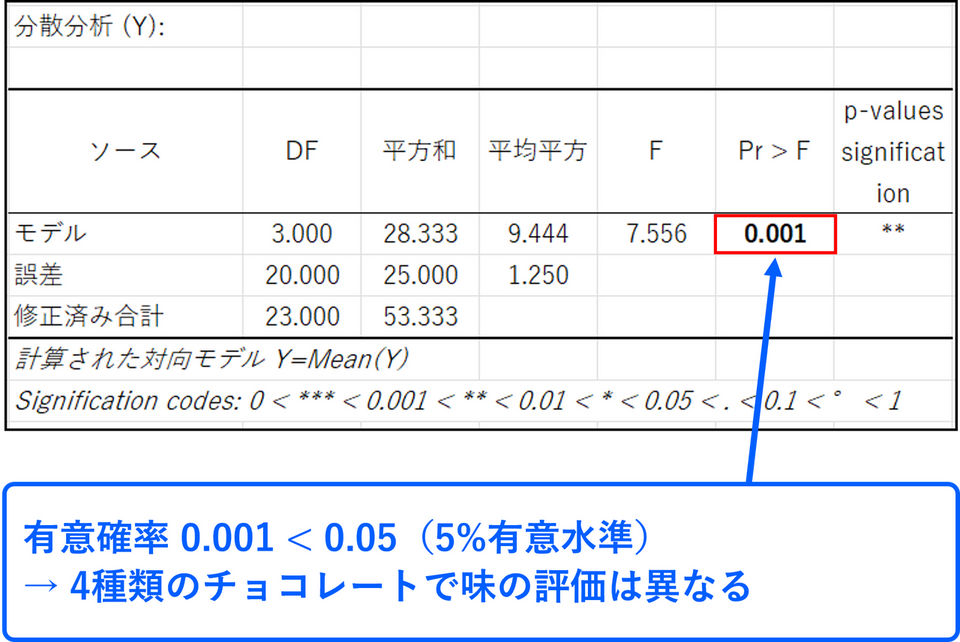
そのほか表内の用語の意味は以下の通りです。
- モデル(グループ間)
水準の違いの効果のことです。各水準の平均と全体平均との差を表しています。要因間、群間、グループ間とも呼ばれます。 - 誤差(グループ内)
各水準内の個体差のことです。各水準内の個別の値と各水準の平均値との差を表しています。「モデル」で説明しきれないものであり、「統計誤差」、「グループ内」とも呼ばれます。 - DF(自由度)
自由に値を取れるデータの数のことです。データ数から1を引いた値が自由度となります。今回の事例の場合、水準の数は「4」であるため、水準の自由度は「3(= 4-1)」となります。誤差の自由度は、各水準内の自由度「5(= 6-1)」に水準数「4」をかけた値となるため、「20(= 5x4)」となります。
- 平方和
偏差(平均値との差)を二乗して合計した値を表しています。モデル(水準間)の平方和であれば、各水準の平均と全体平均の差を二乗した合計値になります。今回の事例の場合は、以下のようになります。
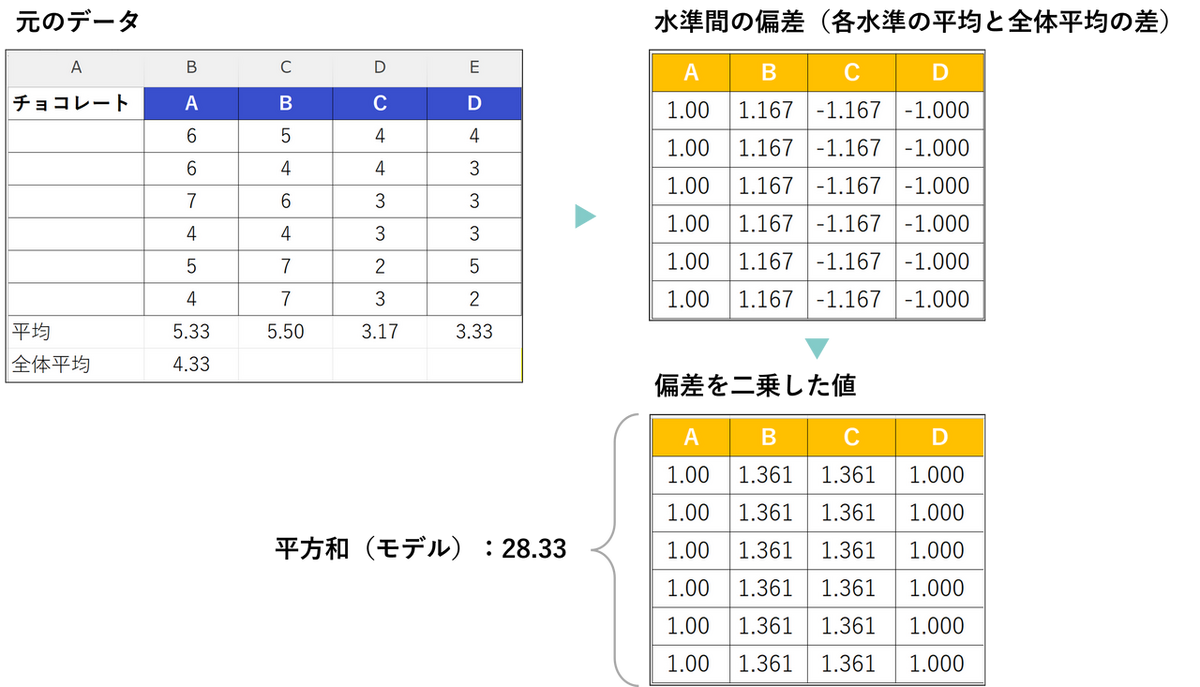
誤差(統計誤差)の平方和であれば、各水準内の個別の値と各水準の平均の差を二乗した合計値になります。
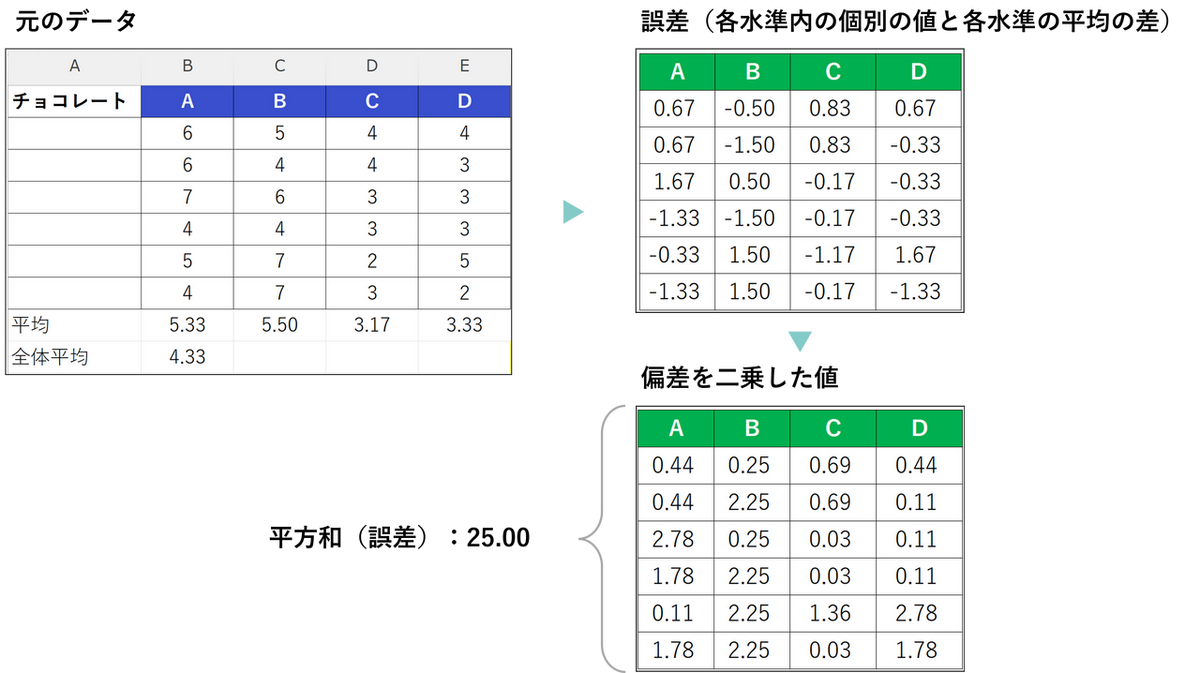
- 平均平方
不偏分散のことです。平方和の値を自由度で割ることで求められます。今回の事例であれば、モデルの平均平方は「9.444(= 28.333÷3)」、誤差の平均平方は「1.250(= 25.00÷20)」 となります。 - F(値)
各データの分散比のことです。F値は「モデルの平均平方÷残差の平均平方」で算出されます。今回の事例であれば、F値は「7.556(= 9.444÷1.250)」 となります。
上記分散分析表の結果から「チョコレートにより味の評価が異なる」ことは分かりましたが、チョコレートA~D のどの組合せで有意差があるのかまでは分散分析では判断できないことに留意する必要があります。つまり、分散分析で明らかにできるのは、各水準の母集団の少なくともどこか一か所は平均値に差があるということだけになります。どの水準間で差があるのかを知りたい場合は、続いてご紹介する多重比較検定の結果を確認します。
多重比較検定
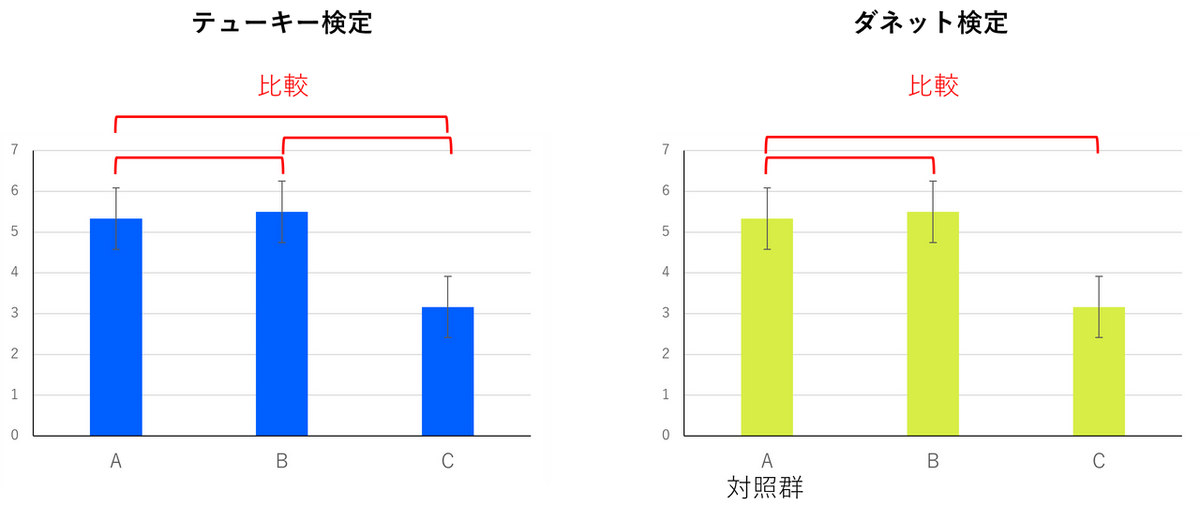
多重比較検定ではどの水準間に有意差があるのかを調べることができます。多重比較検定にはいくつかの方法がありますが、今回のチュートリアルではテューキー検定とダネット検定を実行したため、2つの検定結果が表示されています。
- テューキー検定(Tukey’s test)
データの正規性と等分散性を仮定する多重比較法で、すべての組合せの水準比較を行います。一元配置分散分析の多重比較法として最もよく使用されます。
- ダネット検定(Dunnett's test)
データの正規性を仮定する多重比較法で、1つの対照群(コントロール群とも呼びます)とそのほかの処理群との比較を行います。今回の事例の場合、「チョコレートAが他のチョコレートと評価が異なるかどうかだけ知りたい」というときに役立ちます。すべての組合せの水準比較をするテューキー検定よりも、検出力が高くなります。
テューキー検定(Tukey’s test)
今回の事例では、B-C、B-D、A-C、A-D の組み合わせでp 値が0.05 未満のため、有意差ありと判断できます。
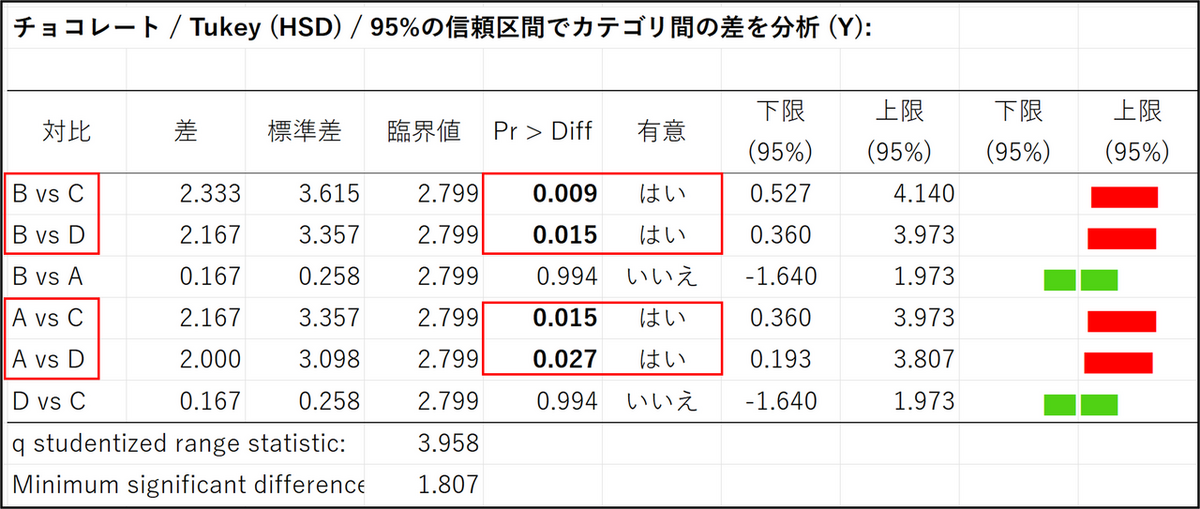
また、差の項目を確認すると、いずれもプラスの値のため、チョコレートA とB は、チョコレートC とD よりも評価が高いと判断できます。一方、A-B とC-D の組み合わせではp 値が「0.05」を上回っているため、味の評価に差があるとは判断できないことになります。
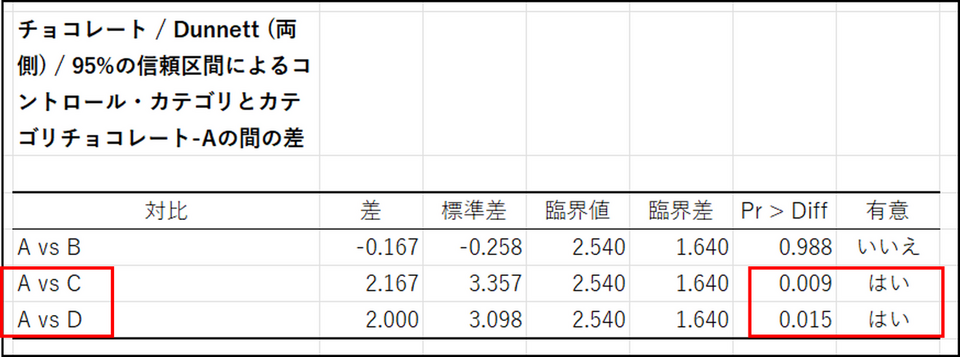
ダネット検定(Dunnett's test)
今回の事例では、分散分析実行時にチョコレートA を対照群として選択したため、チョコレートA とそのほかの水準(B~D)との比較結果が表示されます。結果を確認すると、C とD と比較した場合は、p 値が0.05 未満で、差がプラスの値のため、統計的にチョコレートA の評価が高いと判断できます。
多重比較の問題(補足)
このページでは3グループ以上の標本を利用した母平均の比較には分散分析を用いることを説明してきましたが、2グループの平均値の比較で用いられるt検定を組合せの数だけ実行しても良いのでは?とも考えられます。例えば、講習A、B、C によるテスト結果の差を調べたいのであれば、A と B、B と C、C と A の3回に分けてt検定を実行すれば、良さそうに思えます。
しかし、このようにt検定を繰り返し実行してしまうと、誤って「有意差あり」と判断してしまうリスク(第一種の過誤)が増加してしまうという問題があります。例えば、上記3グループの比較で、5%有意水準のt検定を3回繰り返すと、少なくとも1つの組合せで第一種の過誤を起こす確率は、1 - (どのペアも第一種の過誤を起こさない確率)= 1 - (1-0.05)3 = 0.143 となり、分散分析で全体として設定していた5%有意水準を大きく上回ってしまいます(14%有意水準)。つまり、検定を繰り返し実行すると、検定の評価が甘くなり、本当は差がないのに、偶然に有意差が出てしまうことが簡単に起きてしまうのです。今回ご紹介した分散分析では一度に検定を実行するため、この多重比較の問題を回避することができます。
まとめ
分散分析(ANOVA: Analysis of Variance)は、3グループ以上の平均値に差があるかどうかを統計的に判断するための検定手法です。分散分析にはいくつか種類がありますが、本ページでは1つの因子における水準間の平均値の差を検定する「一元配置分散分析」と「多重比較検定」をご紹介しました。分散分析自体はエクセルに搭載されているデータ分析機能でも実行することができますが、多重比較検定の結果は出力されません。XLSTAT を使うと簡単な操作で分散分析と多重比較検定の結果を一度で確認することができます。一元配置分散分析は、様々な分野のデータ分析に役立つ汎用性の高い検定手法なので、お持ちのデータでどのような結果が得られるかぜひ確認してみてください。
参考文献
-
One-way ANOVA & multiple comparisons in Excel tutorial
https://help.xlstat.com/6598-one-way-anova-multiple-comparisons-excel-tutorial -
阿部真人: データ分析に必須の知識・考え方 統計学入門 仮説検定から統計モデリングまで重要トピックを完全網羅, ソシム, 2021.
-
内田 治: 官能評価の計画と解析, 日科技連出版社, 2024.
-
大村平: 第3版 実験計画と分散分析のはなし, 日科技連出版社, 2024.
-
統計Web. 29-1. 分散分析とは.
https://bellcurve.jp/statistics/course/10006.html -
涌井貞美: まずはこの一冊から 意味がわかる統計解析, ベレ出版, 2013.
XLSTAT の無料トライアル
トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した一元配置分散分析はすべてのライセンスでご利用いただけます。
無料トライアルを申し込む*トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。



