• t 検定とは？
• t 検定における「対応あり（なし）」とは？
• t 検定を実行するためのデータセット
• t 検定の操作手順
• t 検定の結果の解釈
• まとめ
• 参考文献
• XLSTAT の無料トライアル

t 検定とは？

2標本のt 検定は、2つのグループの平均値に差があるかどうかを調べるための統計的手法です。例えば、高血圧に対する新薬を投与したグループと偽薬を投与したグループの血圧を比較して、新薬に効果があるかどうかを検証する際に用いられます。

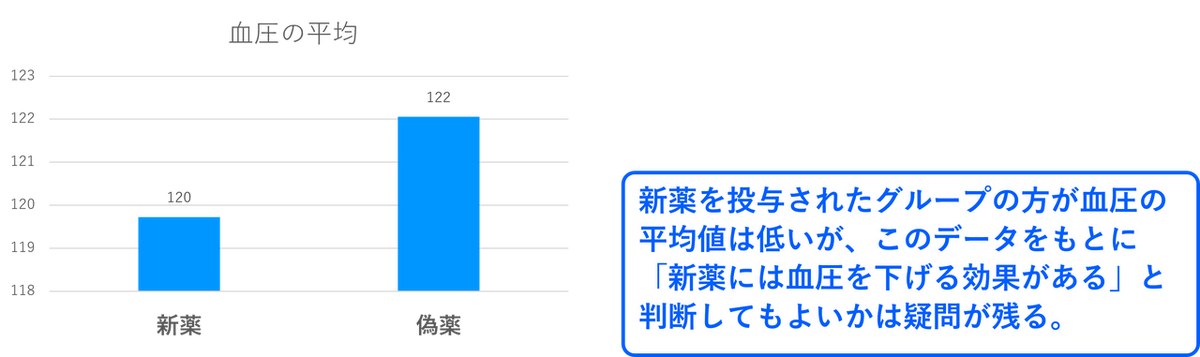
上記の例では新薬を投与されたグループの方が血圧の平均値は低いですが、この結果だけで「新薬には血圧を下げる効果がある」と判断しても問題ないでしょうか。今回取得したデータではたしかに新薬の方が血圧の平均値が低いですが、偶然今回のようなデータが得られたという可能性も考えられます。このように2グループの平均値の差が偶然によるものなのか、それとも統計的に有意な差があるのかという疑問に答えるのが今回ご紹介する「2標本のt 検定」です。

t 検定における「対応あり（なし）」とは？

2標本のt 検定には、「対応あり」と「対応なし」の2種類があります。

対応ありのt 検定
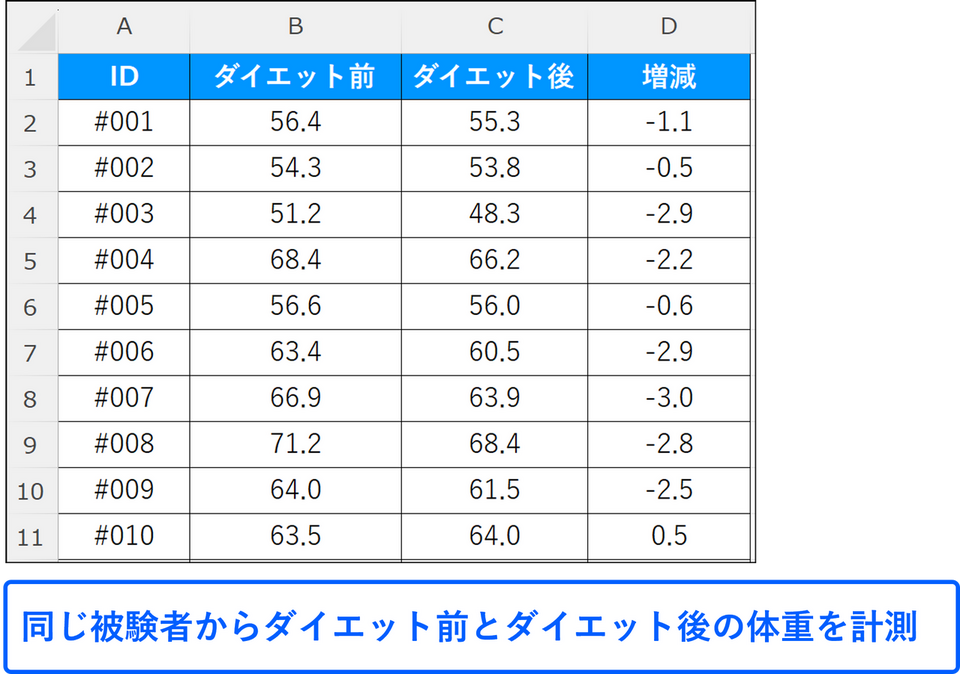
対応ありのt 検定は、同じ被験者に対して2回測定を行う場合に用いられます。例えば、ダイエットプログラムの効果を検証するために、プログラム開始前と開始後の体重を比較する場合などが該当します。

対応なしのt 検定
対応なしのt 検定は、異なる被験者からなる2つのグループを比較する場合に用いられます。例えば、ある学校で行った英語テストの点数がA 組とB 組とで差があるかどうか比較する場合などが該当します。

なお、冒頭でご紹介した新薬と偽薬の血圧データは、それぞれ異なる被験者によるものであるため、「対応なしのt 検定」になります。

t 検定を実行するためのデータセット

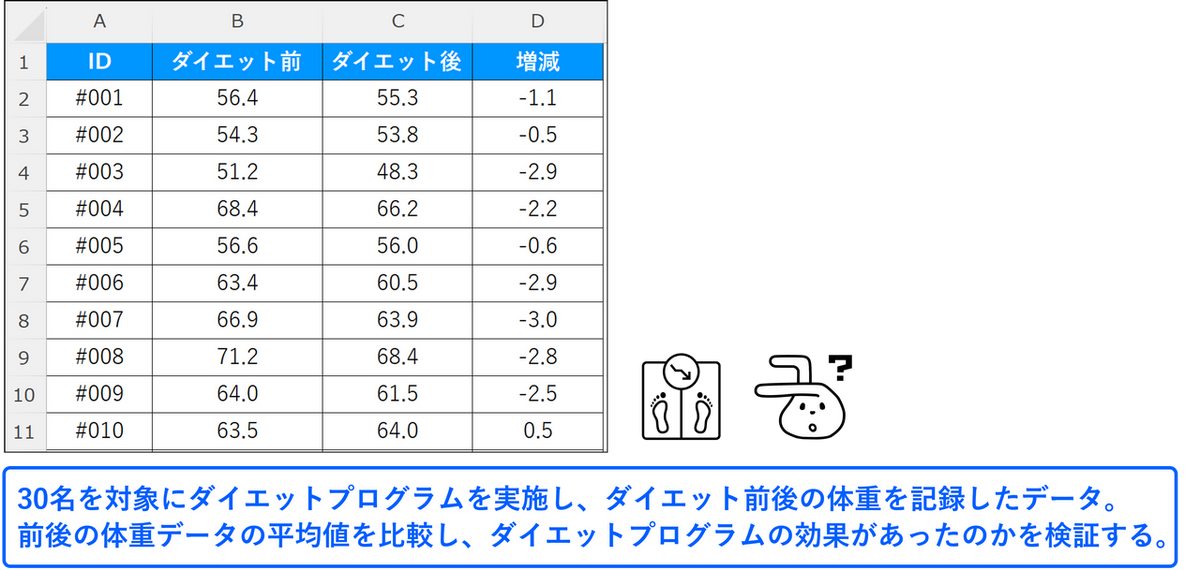
このページでは上記事例で紹介した架空のダイエットプログラムの効果を検証するためのサンプルデータを用いて、XLSTAT でt 検定を実行する方法を説明します。

サンプルデータのダウンロードはこちらから

Two-Sample-T-Test-Dataset.xlsx

t 検定の操作手順

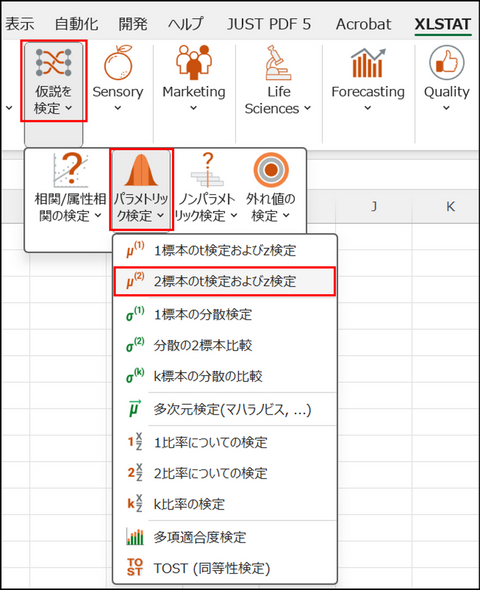
1. XLSTAT を起動し、[仮説を検定] > [パラメトリック検定] > [2標本のt検定およびz検定] を選択します。

   

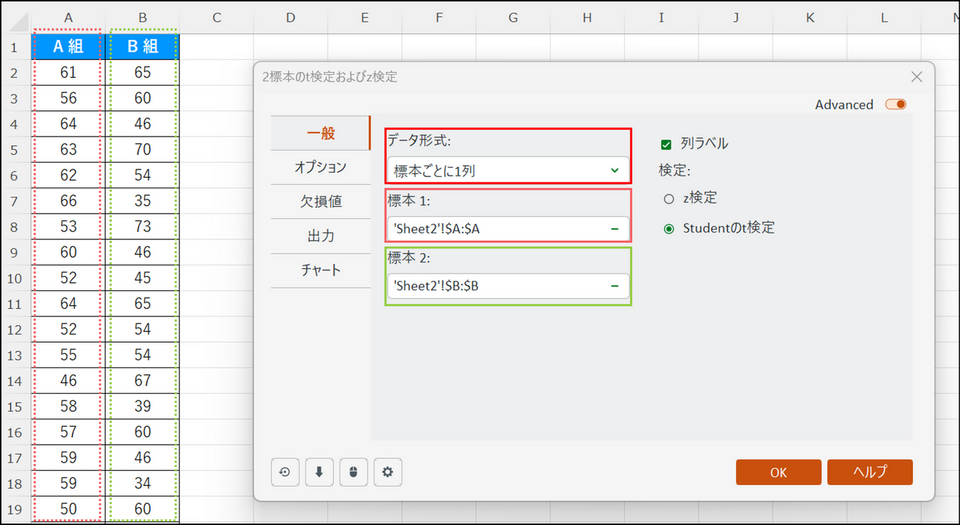
2. ダイアログボックスが表示されるので、下記項目を指定します。

   

   • データ形式：[対応のある標本] を選択
   • 標本1：[ダイエット前] の列データを列名も含めて選択
   • 標本2：[ダイエット後] の列データを列名も含めて選択
   • 列ラベル：列名を含めてデータ選択している場合は、チェックを入れる

   ---

   【補足】対応のないt 検定を実行する場合

   対応のないt 検定を実行する場合は、データ形式で [標本ごとに1列] を選択し、[標本 1] と [標本 2] で各グループのデータを選択します。

   

3. [OK] をクリックすると計算が始まり、結果が別シート（t検定(2標本)）に出力されます。

t 検定の結果の解釈

記述統計

記述統計では各変数のデータの最小値、最大値、平均、標準偏差のデータを確認することができます。

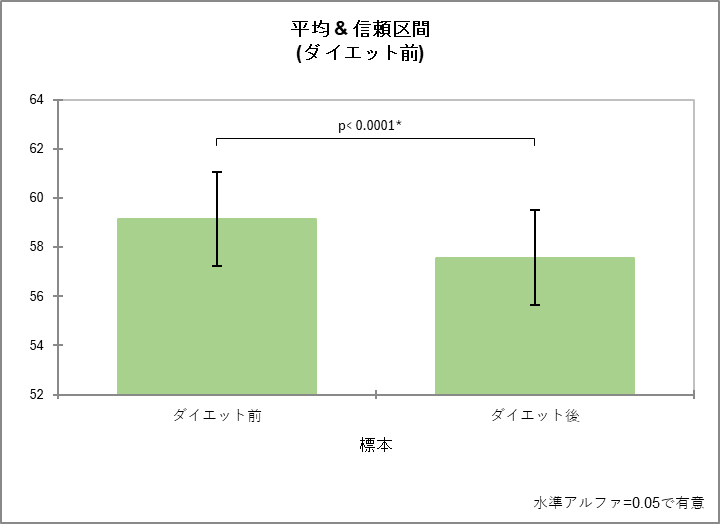
平均の項目を確認すると、平均値が「ダイエット前」の59.148（㎏）から「ダイエット後」は57.569（㎏）に減ったことがわかります。ただ、この値を比較するだけでは偶然による誤差も考えられるので、この後のt 検定の結果で判断します。

正規性検定

正規性検定では、Shapiro-Wilk 検定の結果が表示されます。これはデータが正規分布に従っているかどうかを調べるための検定です。t 検定はデータが正規分布に従っていることを前提としているため、この検定で各グループのデータの正規性を確認します。

正規性検定の帰無仮説と対立仮説は以下の通りです。

• 帰無仮説（H0）：データの分布は正規分布である
• 対立仮説（H1）：データの分布は正規分布ではない

したがって、もし検定結果のp 値が0.05 より小さければ、データの正規性はなく、反対にp 値が0.05 より大きければ、データの正規性はあると判断します。

今回のデータでは、ダイエット前とダイエット後どちらのデータもp値（両側）が0.05 よりも大きいため、データの正規性はあると判断できます。なお、データが正規分布に従っていない場合、t 検定の結果が正しく出力されない可能性があるため注意が必要です。データの正規性がないと判断された場合は、ノンパラメトリック検定を利用する方が安全です。

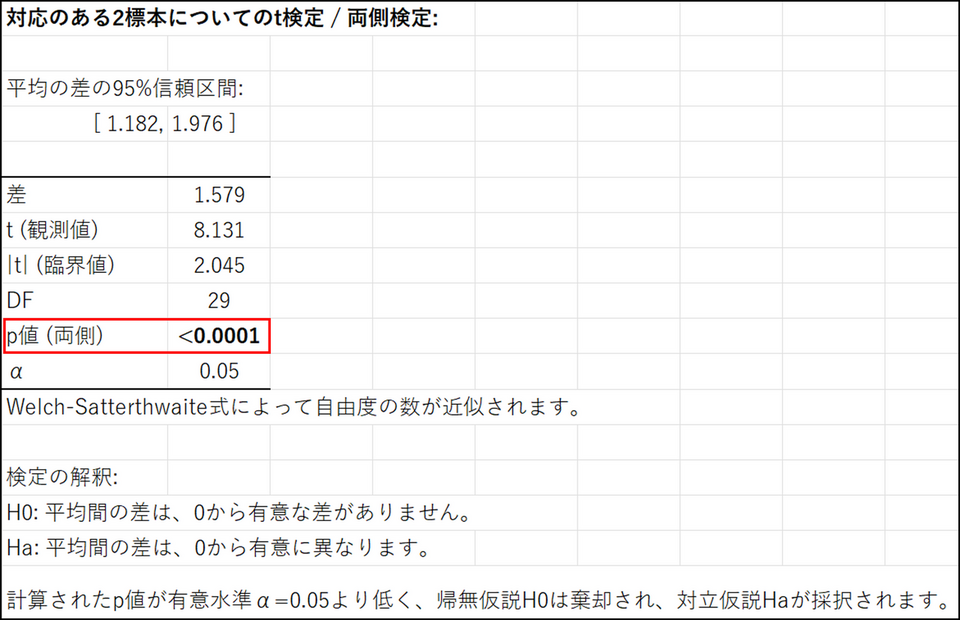
対応のある2標本についてのt 検定

t 検定の結果でもp 値に注目します。今回の場合、p 値は0.0001 を下回っています。つまり、ダイエットプログラムの前後で体重の平均は同じであるという仮定で、今回のデータが偶然得られる可能性は0.01％以下であることを示しています。5%有意水準を採用するなら、p 値が0.05 よりも小さいため、「今回のデータから、ダイエットプログラムに効果があった（有意差あり）」と主張できることになります。

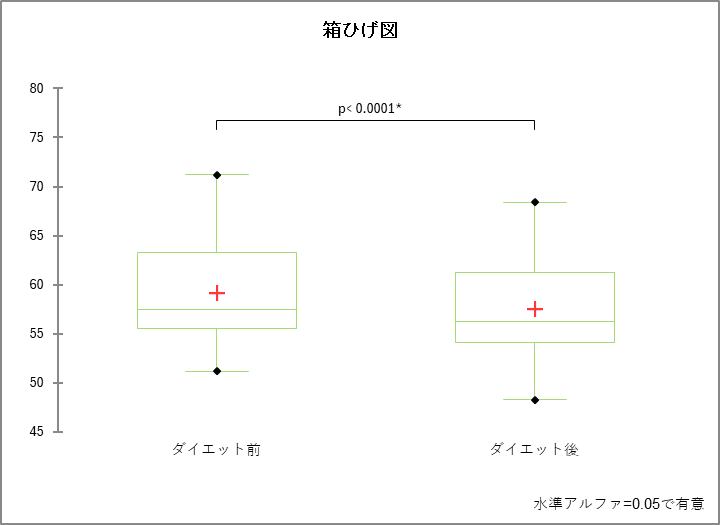
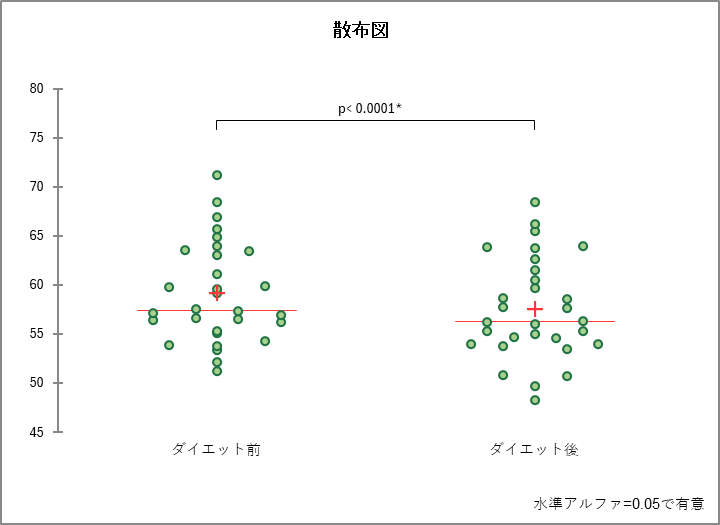
各種グラフ

そのほか出力結果には、t 分布表、箱ひげ図、散布図、平均グラフが表示されます。なお、出力されたグラフは色変更や文字の大きさ変更などの編集が可能です。

まとめ

t 検定は、2つのグループの平均値に有意差があるかを検証するための統計検定であり、医学、薬学、心理学、経済学など様々な分野で広く用いられています。XLSTAT を使用すると、簡単にt 検定を実行し、結果を解釈することができます。また、t 分布表、箱ひげ図、散布図、平均グラフなどのグラフも一緒に表示されるため、視覚的に結果を把握することもできます。

参考文献

• Student's t-test on two paired samples tutorial
  https://help.xlstat.com/6643-students-t-test-two-paired-samples-tutorial
  

• Student's t test on two independent samples tutorial
  

  https://help.xlstat.com/6525-students-t-test-two-independent-samples-tutorial

XLSTAT の無料トライアル

トライアルでは、最上位グレード XLSTAT Premium に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介したt 検定はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。