• 二元配置分散分析とは？
• 二元配置分散分析における「繰り返しのある・ない」とは？
• 交互作用とは？
• 二元配置分散分析を実行するためのデータセット
• 二元配置分散分析の操作手順
• 二元配置分散分析の結果の解釈
• まとめ
• 参考文献
• XLSTAT の無料トライアル

二元配置分散分析とは？

二元配置分散分析とは、ある現象に複数の要因がどのように影響しているのかを調べるための統計手法です。例えば、以下のようなことを調べたい場合に用いられます。

• 「収入」に「性別」と「学歴」という2つの要因がどのように影響しているのか？
• 「ケーキ」と「飲み物」の組み合わせの違いは味の評価に影響するのか？

なお、要因が1つだけの場合の効果を調べたい場合は、「一元配置分散分析」を利用しますが、上記のように2つの要因の場合の効果を調べたい場合は、今回ご紹介する「二元配置分散分析」を利用します。

二元配置分散分析における「繰り返しのある・ない」とは？

二元配置分散分析において、「繰り返しのある・ない」という概念は、分析方法や結果の解釈に大きく関わってきます。

繰り返しのない場合
各条件が1回ずつしか測定されない。つまり、 ある特定の条件の組み合わせに対して、データが1つしか得られない状況を指します。

例：6人のパネリストが4種類のケーキの味を1回ずつ評価する

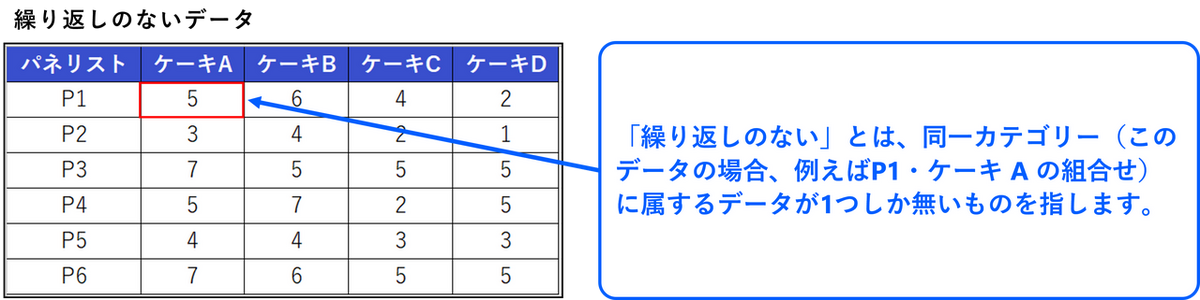
繰り返しのない二元配置分散分析では、それぞれの説明変数が独自に目的変数に与える影響（主効果）を調べることができます。

繰り返しのある場合
各条件が複数回測定される。つまり、ある特定の条件の組み合わせに対して、複数のデータが得られる状況を指します。

例：4種類のパンと2種類の飲み物の味を5名ずつ（合計40名）で評価する（各組み合わせで5回分のデータを取得）

繰り返しのある二元配置分散分析では、主効果に加えて、要因の組み合わせ効果（交互作用）も調べることができます。

交互作用とは？

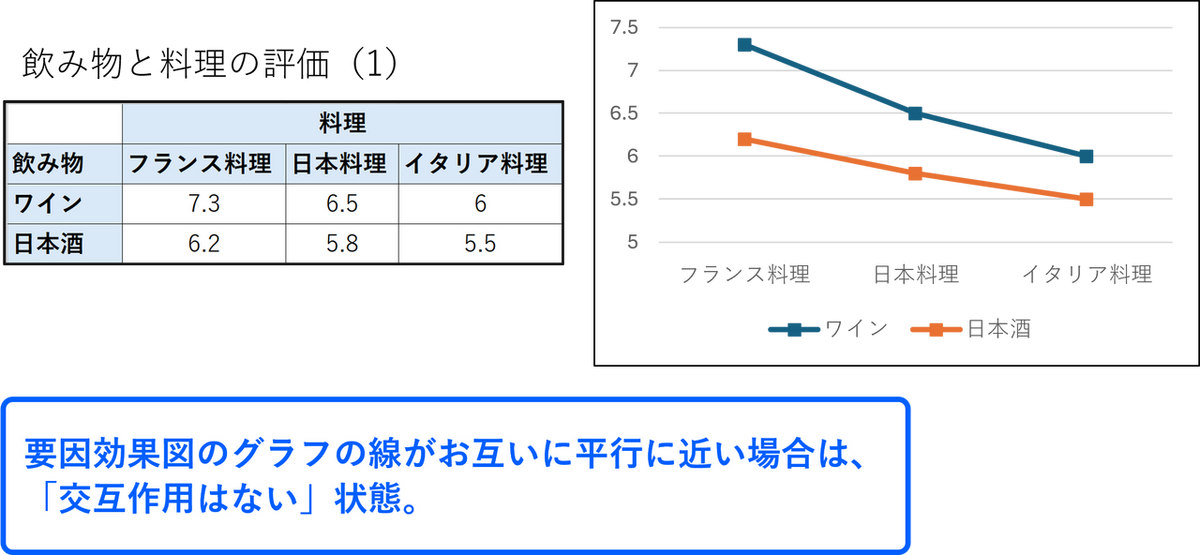
交互作用とはある要因の効果が、別の要因の水準によって変化するという、要因同士の組み合わせ効果のことです。ここでは飲み物と料理の組み合わせについてのアンケート結果を例にとって説明します。「交互作用」を確認する際には、「飲み物」ごとに「平均評価」の折れ線グラフを描きます。横軸は「料理の種類」です。このグラフは「要因効果図」または「交互作用図」と呼ばれます。

データの出典：Excelで学ぶ営業・企画・マーケティングのための実験計画法

交互作用がない場合
以下の事例では要因効果図のグラフの線がお互いに平行に近い状態です。この状態では交互作用があるとはいえません。

交互作用がある場合

以下の事例ではグラフの線が平行でない状態です。飲み物が日本酒のとき、組み合わせる料理が日本料理かそれ以外で評価に対する影響が大きく異なっています。このように、一方の要因の影響が、別の要因の水準によって大きく異なることを「交互作用がある」といいます。

なお、交互作用の影響を分析するにはデータの数が必要になるため、分析対象が「繰り返しのある」データである必要があります。

二元配置分散分析を実行するためのデータセット

本ページでは消費者パネルに、4種類のパン（クロワッサン、あんぱん、カレーパン、メロンパン）と2種類の飲み物（ブラックコーヒー、カフェラテ）を飲食したときの美味しさを7段階で評価してもらったデータを使用します。

この事例での因子は「飲み物の種類」と「パンの種類」の2つで、組合せは4 x 2 = 8 通りあります。また、各組合せの評価を5名ずつ行っているため、合計40名分のデータとなります。要因が2つあることに加えて、同一条件で2名以上が評価したデータになるため、「繰り返しのある」二元配置分散分析になります。今回はこのデータに対してXLSTAT で二元配置分散分析を行い、飲み物の種類とパンの種類の評価について、有意差があるのかどうか、また、2つの因子の交互作用があるのかを確認します。

サンプルデータのダウンロードはこちらから

Two-Way-ANOVA-Sample-Data.xlsm

二元配置分散分析の操作手順

1. XLSTAT を起動し、[発見、説明および予測] > [データ・モデリング] > [ANOVA] を選択します。

   

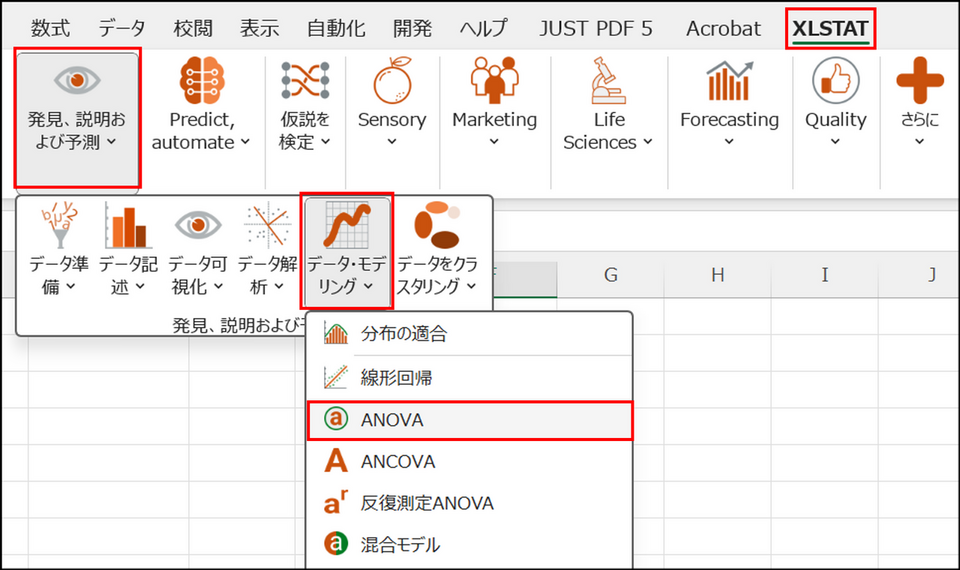
2. ダイアログボックスが表示されるので、下記項目を指定します。

   

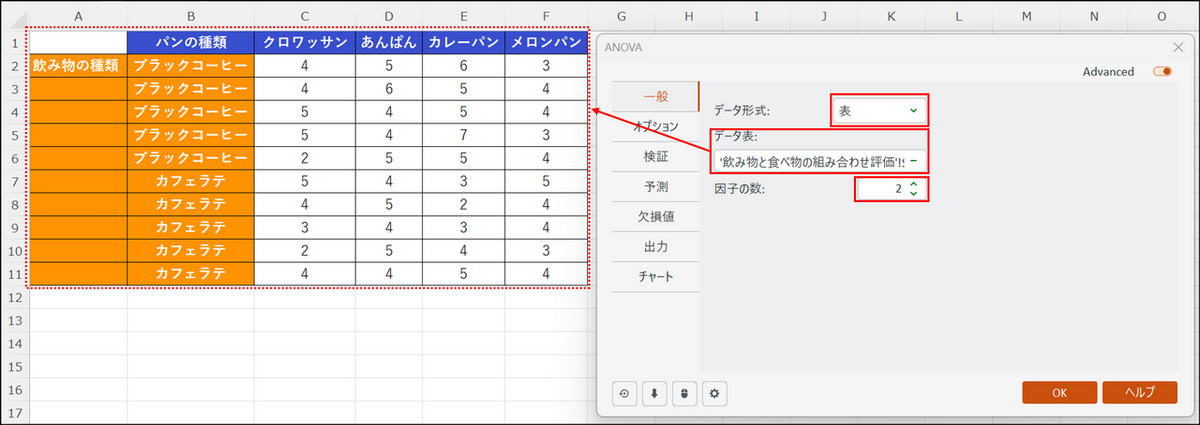
   • データ形式：[表] を選択。列形式のデータであれば、[列] を選択します。
   • データ表：分析対象のデータセルを直接選択
     ※因子名（「飲み物の種類」と「パンの種類」）のセルも含めて選択します。
   • 因子の数：今回因子の数は2つなので、「2」と入力。

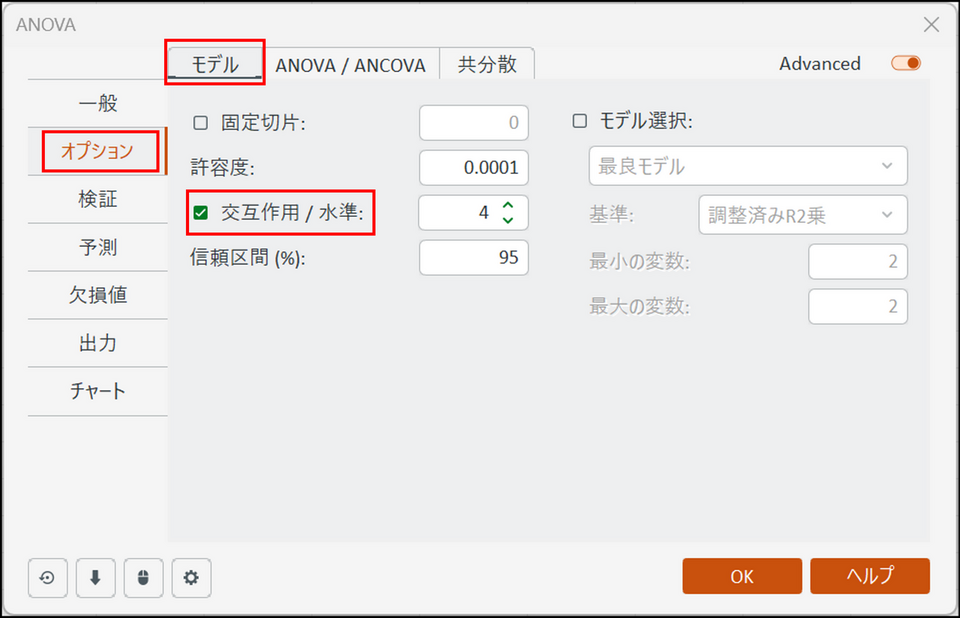
3. [オプション] > [モデル] タブに切り替え、[交互作用 / 水準] の項目にチェックを入れます。

   

4. [OK] をクリックすると、[因子と交互作用] の画面が表示されるので、すべてにチェックを入れて、[OK] をクリックします。

   

5. 計算が実行され、結果が別シート（ANOVA）に出力されます。

二元配置分散分析の結果の解釈

分析結果には、様々な表やグラフが出力されますが、特に重要なのは「分散分析表」と「交互作用」の結果です。

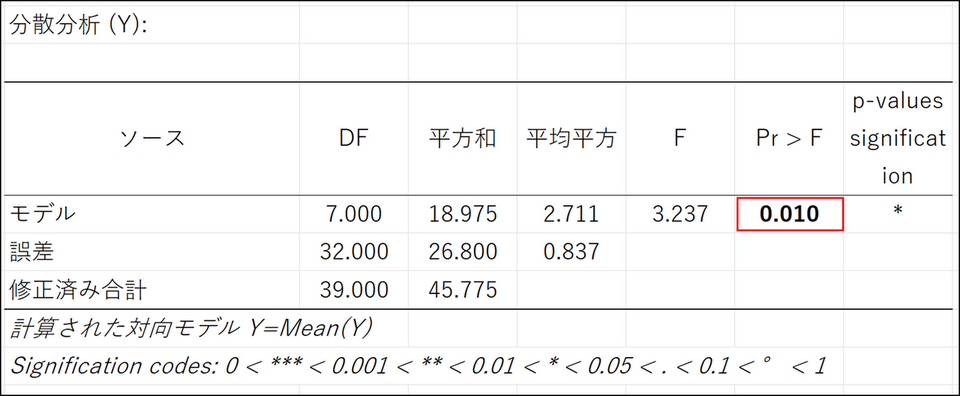
分散分析表

分散分析表ではp 値に注目します。今回の場合、p 値は0.010 となっています。5%有意水準を採用するなら、p 値が0.05 よりも小さいため、因子（飲み物の種類とパンの種類）は美味しさの評価に影響していると判断できます。

分散分析表内の各用語については、下記ページで詳しく説明しています。

XLSTAT による一元配置分散分析（ANOVA）：3種類以上のチョコレートの味の評価を比較する
https://rs.usaco.co.jp/product/xlstat/tips/One-Way-ANOVA-with-XLSTAT.html

分散分析表の下に表示される[Type Iの平方和] の表では因子と交互作用のp 値を確認することができます。

今回のデータでは「飲み物の種類」のp 値は0.032 と0.05 より小さいですが、「パンの種類」のp 値は0.101 と0.05 を上回っています。従って飲み物については、主効果（結果への影響）はありますが、パンについては有意差はないという判断になります。「飲み物の種類*パンの種類」のp 値は0.024 で0.05 より小さいため、交互作用はあるといえます。

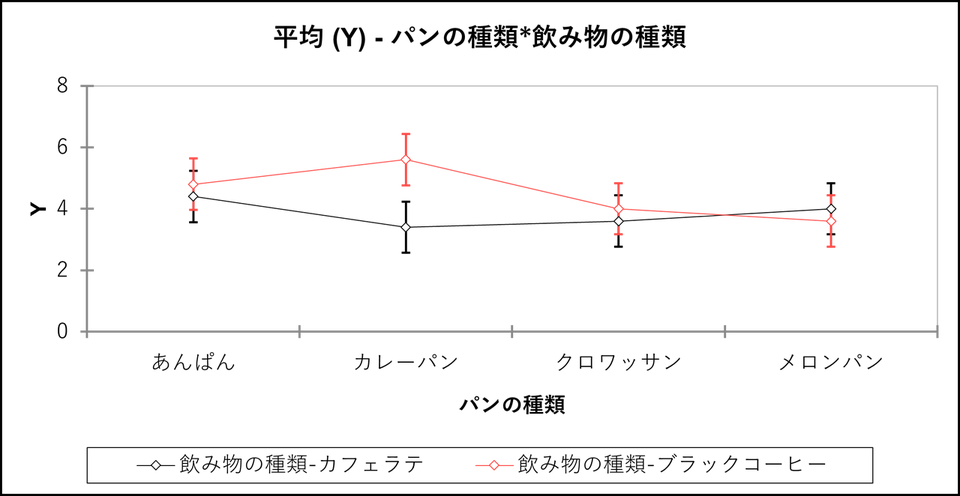
交互作用図

「パンの種類*飲み物の種類:」の項目で各組合せの平均評価とグラフを確認することができます。

平均評価の表ではあんぱん、カレーパン、クロワッサンは、ブラックコーヒーの方が美味しさの評価は高く、メロンパンは、カフェラテの方が美味しさの評価が高いことがわかります。

また、交互作用図を確認すると、飲み物がブラックコーヒーのとき、組み合わせるパンがカレーパンの場合とそれ以外の場合とで評価に対する影響が大きく異なっています。このことからもやはり今回のデータでは交互作用はあるという判断ができます。

まとめ

二元配置分散分析は、複数の要因の影響を同時に調べることができる統計手法です。XLSTAT を利用すると、簡単な操作で各要因の影響を確認できるほか、交互作用図を出力し、要因間の関係性を直感的に理解することができます。様々な分野で利用できる分析のため、ぜひ、ご自身のデータ分析に活用してみてください。

参考文献

• Two-way unbalanced ANOVA with interactions in Excel
  https://help.xlstat.com/6687-two-way-unbalanced-anova-interactions-excel
  
  
• 上田 太一郎 監修: Excelで学ぶ営業・企画・マーケティングのための実験計画法, オーム社, 2006.

XLSTAT の無料トライアル

トライアルでは、最上位グレード XLSTAT Premium に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した二元配置分散分析はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。