• 多変量分散分析（MANOVA）とは？
• 多変量分散分析を実行するためのデータセット
• 多変量分散分析の操作手順
• 多変量分散分析の結果の解釈
• SSCP行列と多変量分散分析で有意差が得られた場合の事後検定について（補足）
• まとめ
• 参考文献
• XLSTAT の無料トライアル

多変量分散分析（MANOVA：Multivariate Analysis of Variance）とは？

多変量分散分析（MANOVA） は、複数の従属変数を同時に分析することで、それらの変数に与える要因（独立変数）の効果を総合的に評価する統計手法です。通常の分散分析では、一度に一つの特性しか扱いませんが、多変量分散分析は、複数の特性値を同時に取り上げて、特性値間の相関を考慮して、因子の効果を検証することができます。

例えば、新製品の候補となるいくつかのシャンプーについて、どのシャンプーが消費者に最も好まれるかを調べるときに、香りや泡立ち、髪の仕上がりなど同時に複数の特性を用いるとします。これらは相互に関連している可能性があり、それぞれの特性について個別に分散分析（ANOVA）を行うよりも、結果が実際の製品評価に即したものになります。

また、分散分析を繰り返すと誤って有意な結果が得られる可能性が増加します。多変量分散分析では一度の分析で全体的な誤差を考慮するため、このようなリスクを減らしてより信頼性の高い結果を得ることができます。

このように、多変量分散分析は、独立変数と複数の従属変数間の関係を同時に分析するため、特性ごとに個別に分散分析を行うよりも効率的に全体像を把握し、より正確かつ信頼性の高い結果が得られるというメリットがあります。

多変量分散分析を実行するためのデータセット

ここでは、20人の消費者パネルに、4種類のシャンプー（新製品A、新製品B、新製品C、新製品D）について、3つの特性（香り、泡立ち、髪の仕上がり）を用いて5段階で評価してもらったデータを使用します。

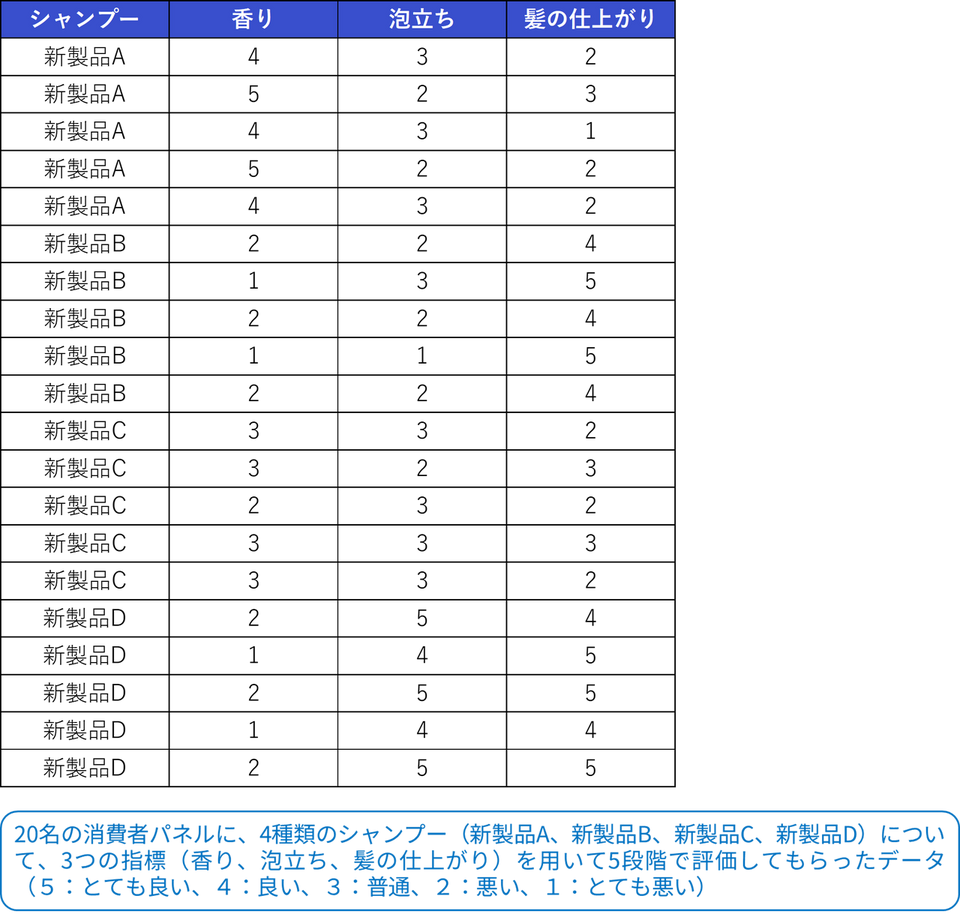
今回は、このデータを使用して、シャンプーの種類によって3つの特性（香り、泡立ち、髪の仕上がり）の評価が有意に異なるのかどうかを明らかにしたいと思います。

なお、今回のサンプルデータでは要因（独立変数）がシャンプーの種類のみなので、「一元配置多変量分散分析」になります。

サンプルデータのダウンロードはこちらから

MANOVA-Sample-Data.xlsm

多変量分散分析の操作手順

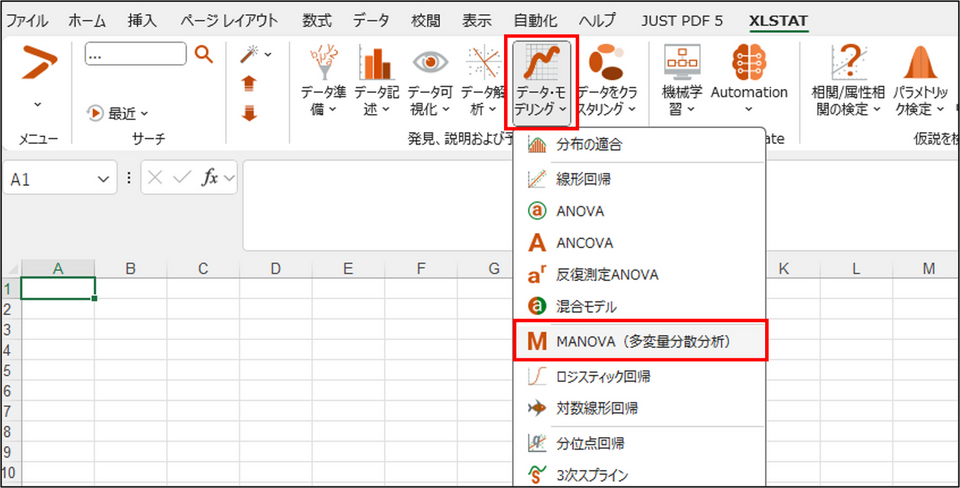
1. XLSTAT を起動し、[データ・モデリング]  > [MANOVA（多変量分散分析）] を選択します。

   

2. ダイアログボックスが表示されるので、[一般] タブで以下のようにデータを選択します。

   

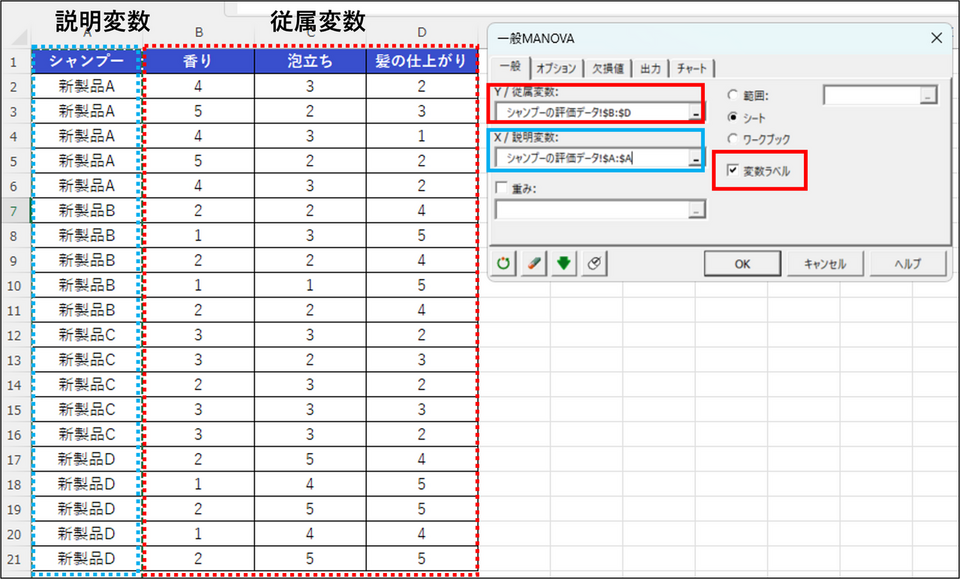
   [オプション] タブでは、今回は説明変数が１つのため交互作用にはチェックを入れません。有意水準のデフォルトは5%です。

   

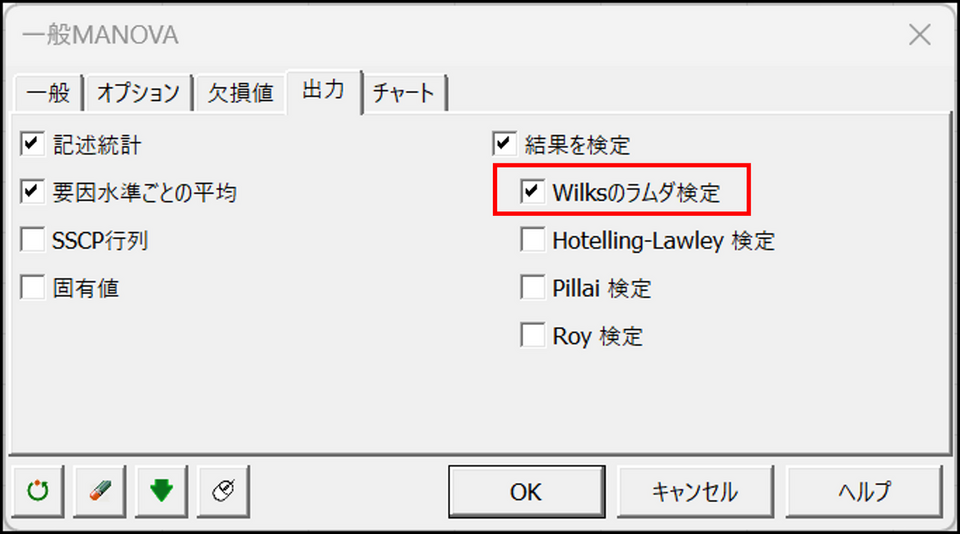
3. [出力] タブで、下の図に示されている項目にチェックを入れます。今回は多変量分散分析においてもっとも一般的に用いられるWilksのラムダ検定を行います。

   

4. [OK] ボタンをクリックします。

5. 計算が実行され、結果が別シートに出力されます。

一元配置多変量分散分析の結果の解釈

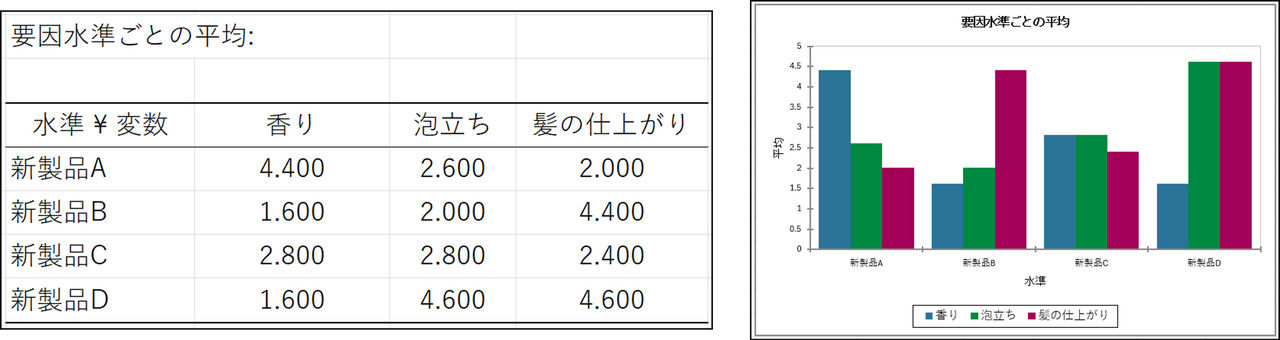
結果にはまず、要因（シャンプーの種類）別に水準（香り、泡立ち、髪の仕上がり）ごとの平均が表とヒストグラムとして出力されます。

これを見ると、シャンプーによって、各特性に傾向があるように見られますが、多変量分散分析によって、統計的に有意な差であるかを判断することができます。

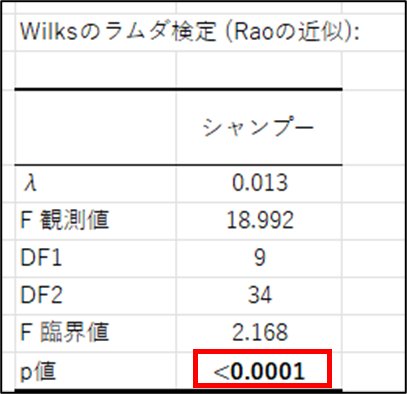
Wilksのラムダ検定の結果より、有意水準の0.05よりも低いp値（<0.0001）が得られたことから、3つの特性のうち少なくとも1つの特性でシャンプーの製品間に統計的に有意な差があることが確認されました。

SSCP行列と多変量分散分析で有意差が得られた場合の事後検定について（補足）

分析を実行する際、[出力]タブから[SSCP行列]を選択すると、以下の３つの行列が表示されます。SSCP行列は平方和（SS）と積和（CP）の行列であり、グループ間およびグループ内の相互作用を大まかに把握するために使用されます。

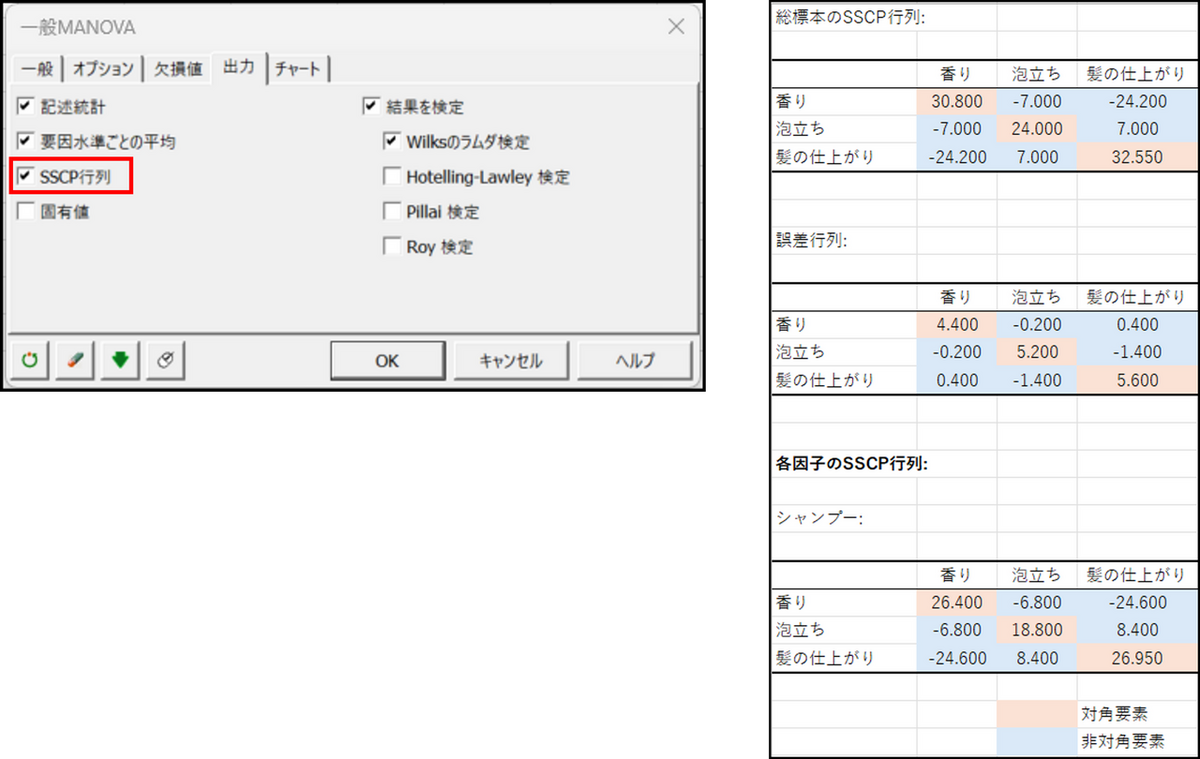
1. 総標本のSSCP行列：
   全データの平方和と積和を含み、データ全体の変動構造を把握することができます。総標本のSSCP行列は、誤差行列と各因子のSSCP行列の合計になり、この分解によって、因子によって説明される変動とグループ内の変動を分離することができます。
   
   
2. 誤差行列：
   グループ間の違いを除外したグループ内の変動を示しています。
   
   
3. 各因子のSSCP行列：
   ここでは「シャンプー」という因子が、グループごとのデータに基づいて、変数（香り、泡立ち、髪の仕上がり）間の変動にどれほど影響を与えているかを示しています。

詳細な説明は省きますが、行列の各要素を通じて以下のような情報が得られます。

• 対角要素：
  平方和（SS）を表し、各変数の分散（変動）がどの程度あるかを示します。各因子のSSCP行列では、対角要素が大きければ因子が変数の変動に大きく寄与していることを示し、誤差行列では、小さいほどモデルの適合度が高いと考えられます。
  
  
• 非対角要素：
  積和（CP）を表し、変数間の共分散、すなわち変数間の相関の強さを示します。非対角要素の符号は変数間の関連性の方向（正の相関または負の相関）を示しています。

今回の事例で見た総標本のSSCP行列では、対角要素（30.800、24.000、32.550）から、シャンプーの新製品A～Dを評価する際、香り、泡立ち、髪の仕上がりの各特性が重要であることがわかりますが、泡立ちの関与がやや低いことが示されています。非対角要素からは、香りと髪の仕上がりに負の相関（-24.200）が存在し、香りの評価が高い場合に髪の仕上がりの評価が低くなる傾向があるという解釈ができます。

多変量分散分析の注意点

多変量分散分析で注意すべきなのは、分析で明らかにできるのは複数の従属変数「全体」に対して、独立変数が有意な影響を与えているか否かということです。

つまり、検定の結果、「有意差あり」と判断された場合でも、具体的にどの従属変数に影響を与えているかまでは多変量分散分析単体では判断できないことに留意する必要があります。

多変量分散分析で有意差があると判断できた後に、どの従属変数が独立変数の影響を受けているのかを詳しく調べたい場合は、個別の特性（従属変数）ごとに分散分析を行うことをお勧めします。

これにより、どの特性において有意差が存在するのかを確認できます。有意差が得られた特性については、多重比較検定を適用することで、どのグループ間に有意差があるのかを特定することが可能です。

多重比較検定については、以下の一元配置分散分析のチュートリアルを参照してください。
https://rs.usaco.co.jp/product/xlstat/tips/One-Way-ANOVA-with-XLSTAT.html

まとめ

多変量分散分析（MANOVA: MANOVA：Multivariate Analysis of Variance）は、1つまたは複数の独立変数によって形成されたグループ間で、複数の従属変数の平均値に統計的に有意な差があるかどうかを検証するための統計手法です。

さらに、統計的に有意な差が見られた場合には、さらなる詳細分析が必要となります。ここでSSCP検定を利用して、変数間の共分散構造を詳細に調べたり、個別の分散分析を行って特定の従属変数に焦点を当てることができます。さらに、多重比較検定を適用することで、どのグループ間に有意な差が存在するかを特定できます。これらの分析は、XLSTATを使用することで効率的に実施することができ、研究の精度を向上させることが期待されます。

参考文献

• Multivariate Analysis of Variance (MANOVA) in Excel tutorial
  https://help.xlstat.com/6393-multivariate-analysis-variance-manova-excel-tutorial
  
  
• BellCurve統計WEB
  https://bellcurve.jp/statistics/

XLSTAT の無料トライアル

トライアルでは、最上位グレード XLSTAT Premium に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した多変量分散分析はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。