XLSTAT による階層型クラスター分析：類似度に基づいて消費者データをグループ分けする

カテゴリ操作方法、活用例最終更新日2025年4月10日

クラスター分析とは？
クラスター分析の種類と使い分け
クラスター分析で使われる用語
階層型クラスター分析の実行過程（理論説明）
階層型クラスター分析を実行するためのデータセット
階層型クラスター分析の操作手順
階層型クラスター分析の結果の解釈
まとめ
参考文献
XLSTAT の無料トライアル

クラスター分析とは？

クラスター分析とは、たくさんのデータから似たもの同士をいくつかのグループ（クラスター）に分類する解析手法です。大量のデータをグループ分けすることで、データの全体像を把握しやすくしたり、データの中に潜むパターンや構造を発見し、新たな知見を得ることにも役立ちます。例えば、顧客の購買履歴データに対してクラスター分析を行うことで、似たような購買行動を示す顧客グループを発見し、それぞれのグループに合わせたマーケティング戦略を立てることができます。

クラスター分析の種類と使い分け

クラスター分析には、大きく分けて階層型クラスター分析と非階層型クラスター分析の2種類があります。

階層型クラスター分析：

データ間の類似度に基づいて階層的なクラスター構造を構築する方法です。個々のデータ点をそれぞれ独立したクラスターとして扱い、最も類似度の高いクラスター同士を順次統合していきます。結果はデンドログラムと呼ばれる樹形図で表され、クラスターの関係性を視覚的に示します。

階層型クラスター分析ではクラスターの数をあらかじめ決めずに、どの段階で線を引くかによってクラスターの数が変わります。

非階層型クラスター分析：

事前にクラスターの数を決めて、データを指定された数のクラスターに分割する方法です。非階層型クラスター分析にはいくつか種類があり、代表的なk-means クラスタリングでは、クラスターの重心と各データ点のクラスターの割り当てを反復計算することで、最適なクラスタリング結果を求めます。

両者の特徴を整理すると以下のようになります。

特徴	階層型クラスター分析	非階層型クラスター分析
アプローチ	階層的にデータを分ける	事前に指定されたクラスター数に基づいて直接データを分割
クラスター数	事前にクラスター数の指定は不要。後から適切な数を選択できる	事前にクラスター数の指定が必要
データ規模と計算コスト	データ数が少ない場合に有効。大規模データでは計算が重い可能性がある。	比較的速く計算でき、大規模データに適している。
代表的な手法	ウォード法、群平均法、最長距離法、最短距離法など	k-means 法、k-medoids 法など

一般的に、データ数が少なく、クラスター数を決められない場合は階層型クラスター分析を選択します。反対にデータ数が多く、事前にクラスター数の目安がある場合には非階層型クラスター分析を選択します。

クラスター分析で使われる用語

クラスター分析では以下の用語が使われます。

個体：
データセット内の個々のデータのこと
クラスタリング：
データを互いに類似したグループ（クラスター）に分割すること
クラスター：
互いに類似したデータ点のグループ
類似度 / 非類似度：
データ点間の類似性または非類似性を表す尺度。距離（ユークリッド距離、マンハッタン距離など）や相関係数などが用いられます。
デンドログラム：
階層的クラスタリングの結果を樹形図で表したもの。クラスター間の距離やクラスタリングの過程を視覚的に理解できます。

階層型クラスター分析の実行過程（理論説明）

階層型クラスター分析をどのような手順で行うのかを簡単な例を用いて説明します。次のデータは、あるクラスの5人の生徒における国語と数学のテスト点数表（10点満点）とそれを散布図で示したものです。

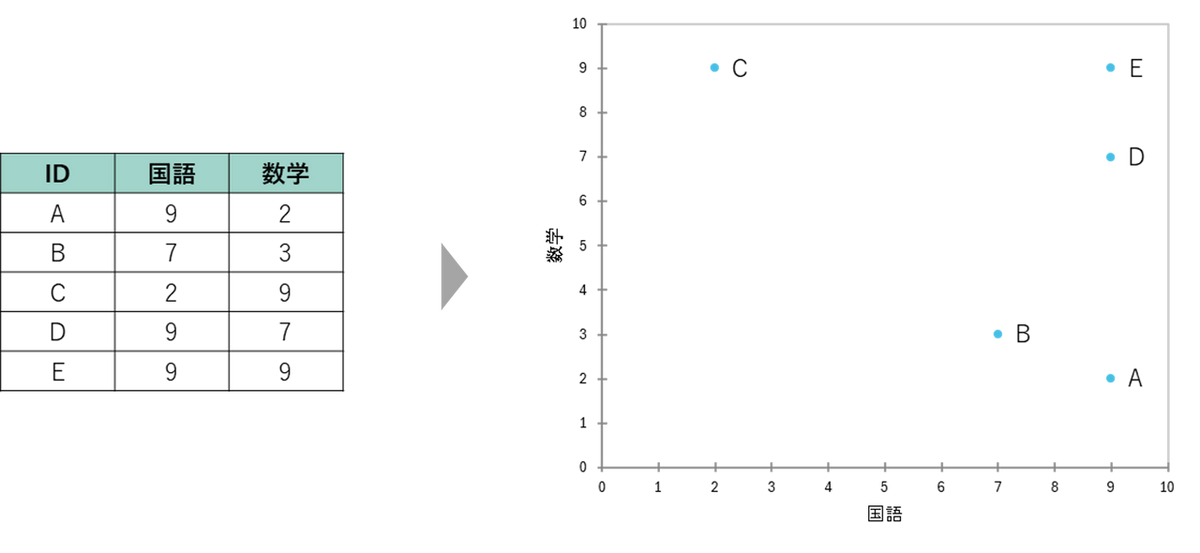
1. 距離行列の計算

クラスター分析ではまず個体間の距離を計算します。個体間の距離を測る方法はいくつかありますが、ユークリッド距離が最も一般的な距離尺度で、2点間の直線距離を計算します。ユークリッド距離では距離が短いほど、データ間の類似性が高く、同じクラスターに分類される可能性が高いという解釈になります。ユークリッド距離は、各変数の差の2乗和の平方根を計算することで求められます。例えば、上記AとB のユークリッド距離は以下のように計算します。

なお、上記事例は2変数ですが、変数の数が増えても、基本的な考え方は変わりません。

3次元の場合：

n次元の場合:

上記の計算式をもとに全ての個体間の距離を計算し、距離行列を作成します。その結果は以下の通りです。

表の右上部分が空白なのは、対称行列であるためです。例えば、生徒A と生徒B の距離は、生徒B と生徒A の距離に等しくなります。

2. クラスターの形成

距離行列が作成できたら、個体間の距離が近いものから順に結合していきます。今回の例では「DとE」の距離が最小（2.0）なので、「D」と「E」を結合し、クラスター（DE）を形成します。

続いて、新たに作成したクラスターDE と残りのすべての個体間の距離を計算します。クラスターと個体、クラスターとクラスターの距離を測る方法にも様々な種類がありますが、ここでは説明を簡便にするため、最長距離法を使います。最長距離法は、クラスター内の最も離れた点同士の距離に基づいてクラスター間の類似度を測ります。

最長距離法に基づいて、クラスターDE と残りの個体間の距離を再計算した結果は以下の通りです。

上記距離行列から最も距離が近いのは「AとB」です。したがって、「A」と「B」を結合し、再度ユークリッド距離を計算します。

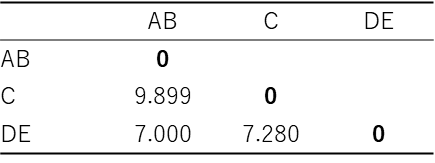
上記距離行列から最も距離が近いのは「AB」と「DE」です。したがって、「AB」と「DE」を結合し、再度ユークリッド距離を計算します。

最後にABDEとC を結合して最終的に1つのクラスターとなります。

3. デンドログラムの作成

上記のクラスターの形成過程をデンドログラムで表現します。

D と E を結合（距離：2.00）
A と B を結合（距離：2.36）
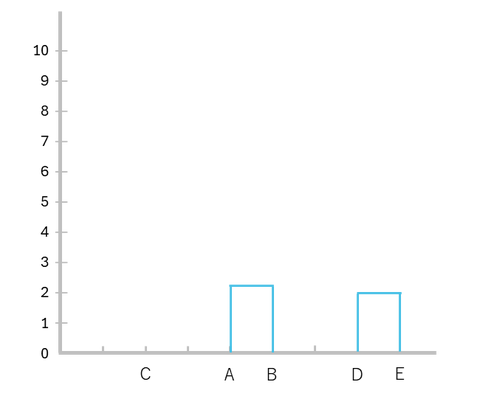
AB とDE を結合（距離：7.00）
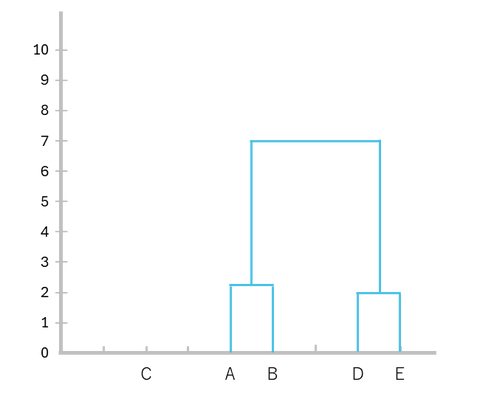
ABDE とC を結合（距離：9.89）

以上でデンドログラムが完成しました。このデンドログラムを下から眺めることでどの個体がどの距離で結合していったのかを確認することができます。

補足：クラスター間の距離について

上記事例ではクラスター間の距離を測る方法として最長距離法を利用しましたが、距離の測定方法はそれ以外にもいくつか存在します。それぞれの方法でクラスターの併合の仕方が異なり、分析結果に影響を与える可能性があるため、データの性質に応じて距離の基準を決めることが重要です。

測定方法	概要
最短距離法 (Single Linkage)	クラスターに属する個体のうち、最も近い個体間の距離をクラスター間の距離とする方法
最長距離法 (Complete Linkage)	2つのクラスターに属する個体のうち、最も遠い個体との間の距離をクラスター間の距離とする方法
群平均法 (Average Linkage)	2つのクラスターに属する対象間の組み合わせの距離を求め、その平均値をクラスター間の距離とする方法
重心法 (Centroid Linkage)	各クラスターの重心間の距離をクラスター間の距離とする方法
ウォード法 (Ward's Method)	クラスター内平方和の増加量が最小になるようにクラスターを併合する方法

階層型クラスター分析を実行するためのデータセット

このページでは、50名の消費者に対して現在利用しているスマートフォンについて5段階で評価してもらったデータを使用します。評価項目は、総合満足度、価格、重さ、デザイン、性能の5つです。

今回はこれら5つの変数について、どのような特徴をもつ消費者がいるのかを階層型クラスター分析で確認します。

サンプルデータのダウンロードはこちらから

Hierarchical-Cluster-Analysis-Sample-Dataset.xlsm

階層型クラスター分析の操作手順

XLSTAT を起動し、[発見、説明および予測] > [データをクラスタリング] > [凝集型階層クラスタリング (AHC)] を選択します。
ダイアログボックスが表示されるので、[一般] タブで以下のようにデータを選択します。
- オブザベーション/変数：評価データの変数列を列名も含めて選択
- 近接タイプ：[非類似度] を選択し、[ユークリッド距離] を選択
- 凝集法：[Ward距離] を選択
- 列ラベル：列名を含めてデータ選択している場合は、チェックを入れる
- 行ラベル：チェックを入れ、番号列を選択
[オプション] タブに切り替え、以下の項目を指定します。
- [行をクラスタ] にチェックを入れる
- [打ち切り] にチェックを入れ、[Hartigan index (adpt.)] を選択し、最適なクラスター数を自動的に決定します（クラスター数の範囲は2 から6 に設定）。
【補足】中心化 / 尺度化のオプションについて
クラスター分析で単位の異なる変数をそのまま投入すると、結果が単位の大きな変数に強く影響されてしまう可能性があるため注意が必要です。例えば、身長（cm）と年収（万円）を同時にクラスター分析に投入する場合、一般的に年収の値は身長の値よりも大きいため、年収によって結果が左右され、身長の違いがほとんど考慮されなくなってしまいます。そのため、分析対象のデータ内に単位の異なる変数が含まれている場合には、[中心化 / 尺度化] のオプションを有効にしてデータを標準化しておきます。今回のデータではすべての変数が5段階評価のため、このオプションは不要です。
[出力] タブに切り替え、以下の項目にチェックを入れます。
[チャート] タブに切り替え、以下の項目にチェックを入れます。
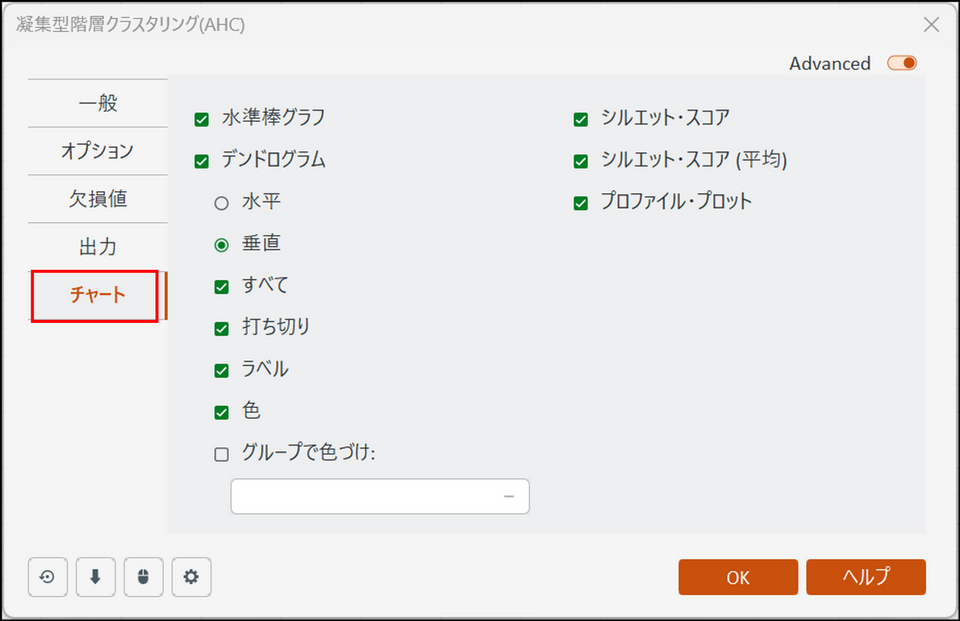
[OK] をクリックすると計算が始まり、結果が別シート（AHC）に出力されます。

階層型クラスター分析の結果の解釈

結果には複数の表やグラフが出力されますが、以下の点に着目して結果を解釈します。

記述統計

記述統計では各変数の最小値、最大値、平均、標準偏差のデータを確認することができます。平均に注目すると、「重さ」はほかの項目と比較して低く、標準偏差も小さいようです。

近接行列（親近度行列） (ユークリッド距離)

近接行列では個体間の距離を確認できます。クラスター分析では、この距離に基づいて、類似性の高い個体を同じクラスターに、類似性の低い個体を異なるクラスターに分類します。

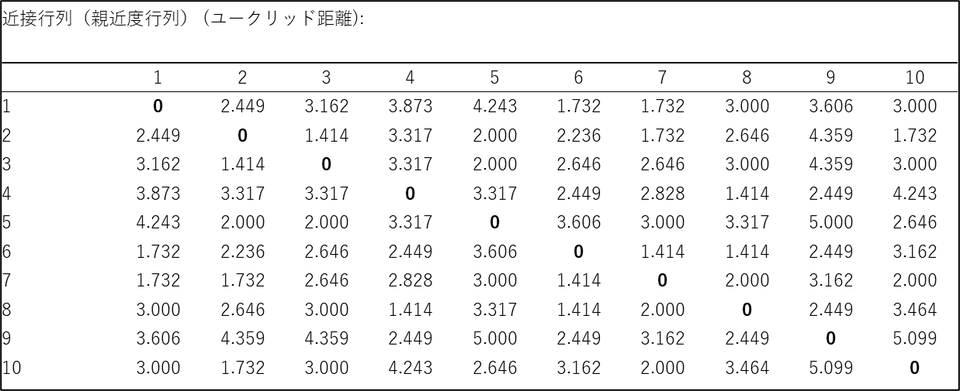
個体間の距離を測る方法はいくつかありますが、今回の結果に表示されているユークリッド距離は最も一般的な距離尺度で、2点間の直線距離を計算します。ユークリッド距離では距離が短いほど、データ間の類似性が高く、同じクラスターに分類される可能性が高いという解釈になります。

ノードの統計量

「ノードの統計量」では、デンドログラム中の連続するノードの情報を表示します。ノードとはデンドログラム上のデータの結合を示す点のことです。この表を下から見ていくことで、データまたはクラスター同士がどの距離（=水準）で結合していったのかを確認することができます。

なお、ノードのインデックス（識別子番号）は、元のデータ数に＋1 した番号から付与されていきます。今回分析対象のデータは50名分であるため、最初のデータ同士が結合した点であるノードのインデックスは51 となっています。

水準棒グラフ

水準棒グラフでは「ノードの統計量」のノードを縦軸、水準を横軸に示しています。棒の高さが急激に上昇している箇所は、異質なクラスター同士が統合されたことを意味し、クラスタリングの妥当性を判断する材料となります。適切なクラスター数をいくつにするかは続いて表示される指標も確認しながら判断します。

指標の推移

「指標の推移」ではクラスタリングの品質を評価するための各種指標がクラスター数ごとに表示されます。

クラスター分析では、この後に紹介するデンドログラムも確認して、適切なクラスター数を判断しますが、これらの指標を手がかりにすることも可能です。

シルエット指標（シルエットスコア）
シルエット指標は、-1から1までの範囲の値を取り、1に近いほど、クラスタリングが良好であることを示します。0 に近いほど、データポイントがクラスターの境界付近に位置し、どちらのクラスターに属するかが曖昧であることを示します。-1 に近いほど、クラスタリングが不適切であることを示します。

Hartigan指標 (H)
Hartigan指標（ハーティガン指数）は、クラスター内の分散とクラスター間の分散の比率に基づいて計算されます。通常クラスター数を増やしていくと、クラスター内の分散は減少し、クラスター間の分散は増加します。ハーティガン指数は、この変化の度合いを数値化し、クラスター数を増やすことによる効果がどれだけあるかを示します。ハーティガン指数の値が低いほど、クラスターがよりコンパクトで、クラスター間の分離が大きく、クラスタリングが優れていることを示します。

H(k-1) - H(k)
この指標は、クラスター数を1つ増やした際に、ハーティガン指数がどれだけ減少するかを示しています。H(k-1) はクラスター数(k-1) でのハーティガン指数、H(k) はクラスター数(k) でのハーティガン指数です。この差分が大きい場合、クラスター数を増やすことによって、クラスタリングの結果が大きく改善されたことを意味します。一方、差分が小さい場合、クラスター数を増やしても、クラスタリングの結果は有意に改善されないことを意味します。

XLSTAT では上記H(k-1) - H(k) の値が最大となるクラスター数を採用します。今回の結果ではクラスター数が2 のときに最大となるため、太字で表記されています。

凝集型階層クラスタリング(AHC)

デンドログラムでクラスタリングの結果を確認できます。縦軸は距離を表しており、低い位置で合流しているものは類似度が高く、高い位置で合流しているものは類似度が低いという解釈になります。

また、上述の指標に基づき適切なクラスター数で自動的に色分けされます。今回のデータではクラスター数を2つに分けるのが最適と判断されたため、C1 とC2 で色分けされています。

クラスタ・セントロイド

クラスターごとに各変数の平均値と分散を確認することができます。クラスタ内分散はクラスターの同質性を表し、値が小さいほどクラスター内のデータが似ていることを意味します。

オブジェクトごとの結果

各データごとにクラスターの情報とシルエットスコアが表示されます。

シルエットスコアが1 に近いほど、そのデータが属するクラスターに適合していることを意味します。値がマイナスの場合は、そのデータがクラスターにあまり適合していないことを示唆しています。

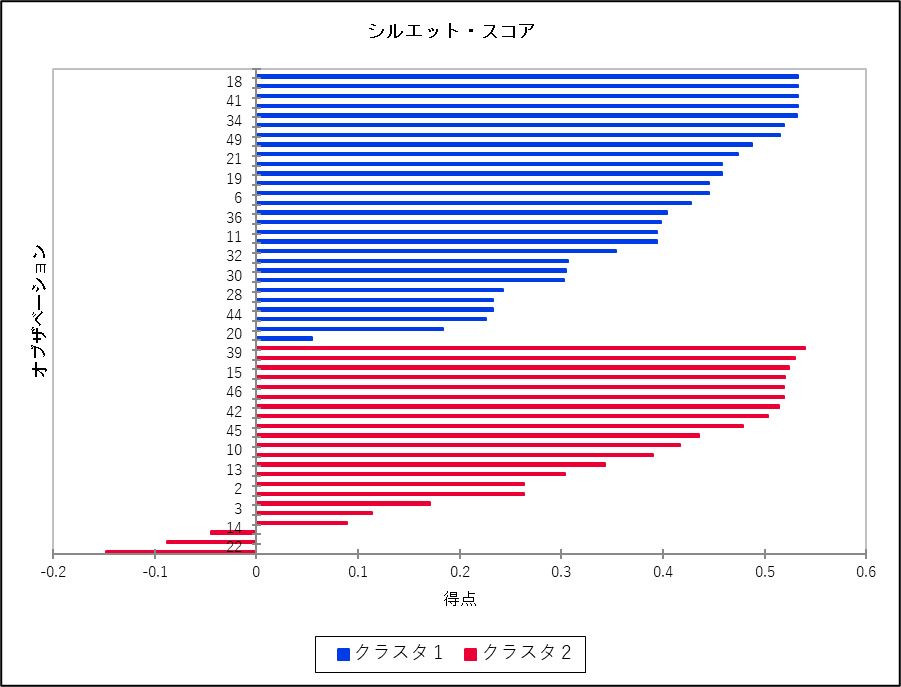
シルエット・スコア

各クラスタのシルエットスコアを降順にソートして表示しています。クラスター全体のシルエットスコアの分布を確認することで、クラスタリングの品質を評価できます。

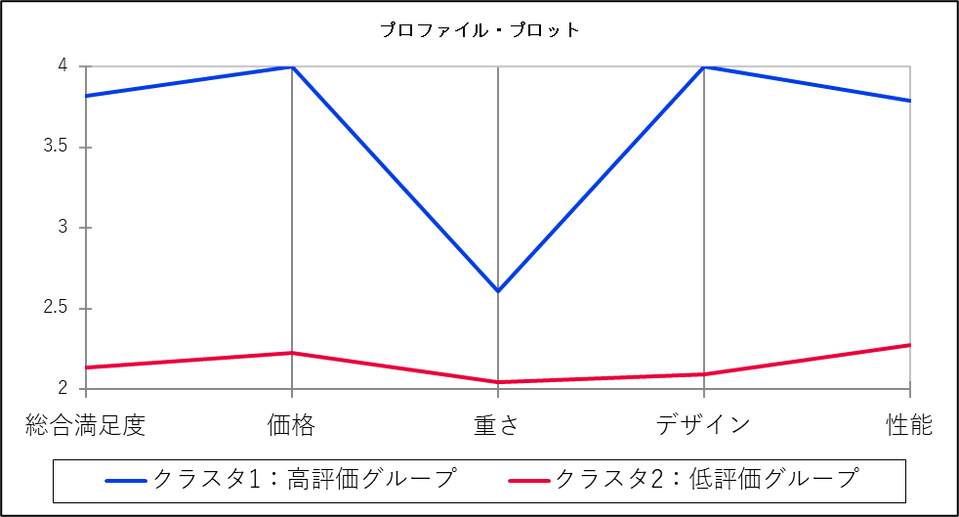
プロファイル・プロット

プロファイルプロットでは、クラスターごとに変数の平均値をグラフで表示しています。

各クラスターの線の形状を比較することで、クラスター間の特性の違いを把握できます。例えば、あるクラスターの線が特定の変数で高い値を示し、別のクラスターで低い値を示していれば、その変数において明確な違いがあると言えます。今回の事例ではいずれの変数もクラスタ1 の方が平均値が高いですが、「重さ」については両者で大きな差はないようです。

なお、クラスター分析で得られたクラスターには適切な名前を付けておくことで、クラスターの特徴が伝わりやすくなり、その後の意思決定にも役立ちます。今回の結果ではクラスタ1 は多くの側面で高い評価を得ているユーザー層と考えられるのに対し、クラスタ2 は現在のスマートフォンに対して不満を感じているユーザー層と考えられます。そのため、クラスタ1 は「高評価グループ」、クラスタ2 は「低評価グループ」と名づけることができそうです。

まとめ

階層型クラスター分析は、データ内の類似性に基づいてデータを階層的なクラスターに分類する分析手法です。この手法を用いることで、大量のデータを整理し、データに潜む構造やパターンを発見することができます。特に、顧客の購買行動分析や市場調査など、様々な分野で意思決定を支援する強力なツールとなります。XLSTAT を使用することで、階層型クラスター分析を効率的に実行し、結果を視覚的に分かりやすく表示することが可能です。ぜひXLSTAT の階層型クラスター分析機能を活用し、データ分析の幅を広げてみてください。

参考文献

Agglomerative Hierarchical Clustering (AHC) in Excel
https://help.xlstat.com/6507-agglomerative-hierarchical-clustering-ahc-excel
阿部真人: データ分析に必須の知識・考え方　統計学入門　仮説検定から統計モデリングまで重要トピックを完全網羅, ソシム, 2021.
統計Web. 7-4. 階層型クラスター分析1.
https://bellcurve.jp/statistics/course/10006.html
平井明代: 教育・心理系研究のためのデータ分析入門～理論と実践から学ぶSPSS活用法～第2版, 東京図書, 2017.
涌井良幸: ゼロからのサイエンス多変量解析がわかった！, 日本実業出版社, 2009.

XLSTAT の無料トライアル

トライアルでは、最上位グレード XLSTAT Premium に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した階層型クラスター分析はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。