• 因子分析とは？
• 因子分析を実行するためのデータセット
• 因子分析の操作手順
• 因子分析の結果の解釈
• まとめ
• 補足1：抽出法と回転法
• 補足2：用語の説明
• 補足3：主成分分析と因子分析の違い
• 参考文献
• XLSTAT の無料トライアル

因子分析とは？

因子分析とは、多くの観測データ（実際に測った項目）の背後にある、いくつかの共通した特徴や傾向（＝「因子」と呼ばれる、直接は測れない隠れた要素）を見つけ出すための統計手法です。

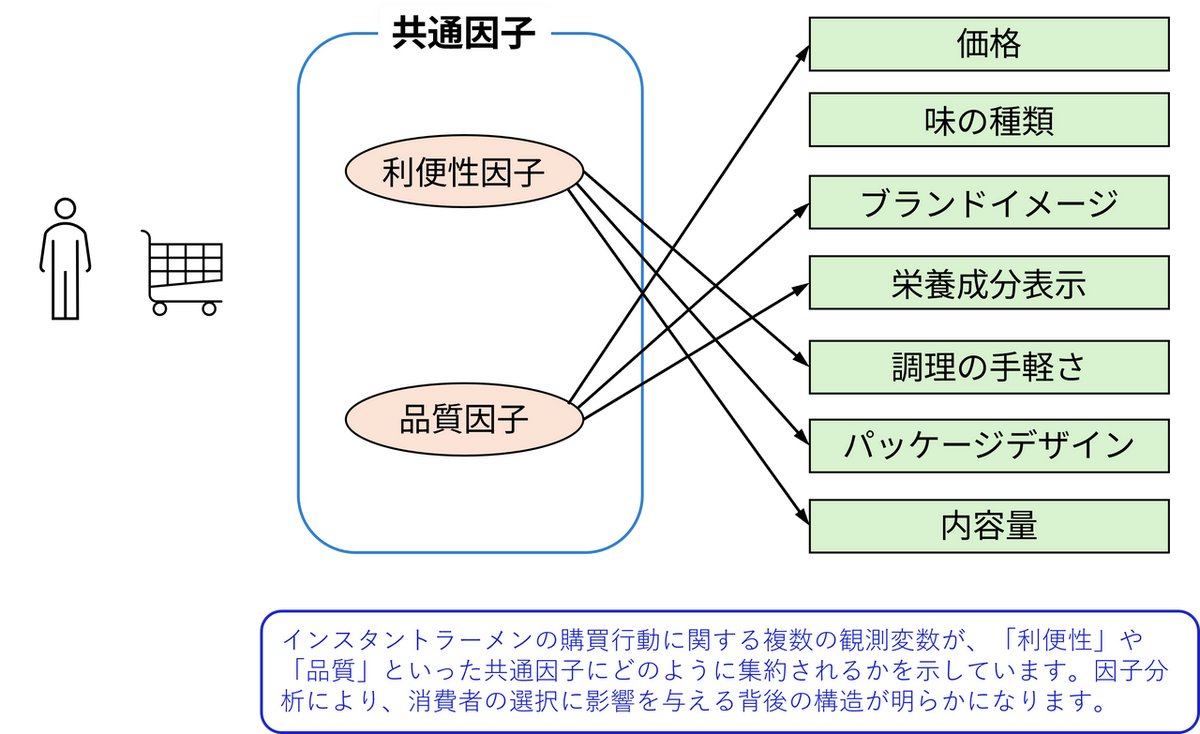
例えば、インスタントラーメンの購買行動を分析したいとします。

スーパーマーケットやコンビニのPOS データからは、「価格」や「味の種類」ごとの販売状況がわかります。さらに、消費者へのアンケート調査からは、「ブランドイメージ」「栄養成分表示」「調理の手軽さ」「パッケージデザイン」「内容量」など、購入時に重視するポイントについての情報を集めることができます。

これらの情報（観測変数）は一つひとつ見るとバラバラですが、実は「似たような理由」で選ばれている可能性があります。

たとえば、「調理の手軽さ」や「パッケージデザイン」「内容量」は、「利便性」という共通の要素でまとめられるかもしれません。また、「価格」や「ブランドイメージ」「栄養成分表示」は、「品質」への期待につながっているかもしれません。

このように、複数の項目の背後にある「共通する考え方」や「価値観」を見つけて整理するのが因子分析です。

因子分析を使えば、「なぜその商品が選ばれたのか」を、よりシンプルでわかりやすい形でとらえることができます。

因子分析を実行するためのデータセット

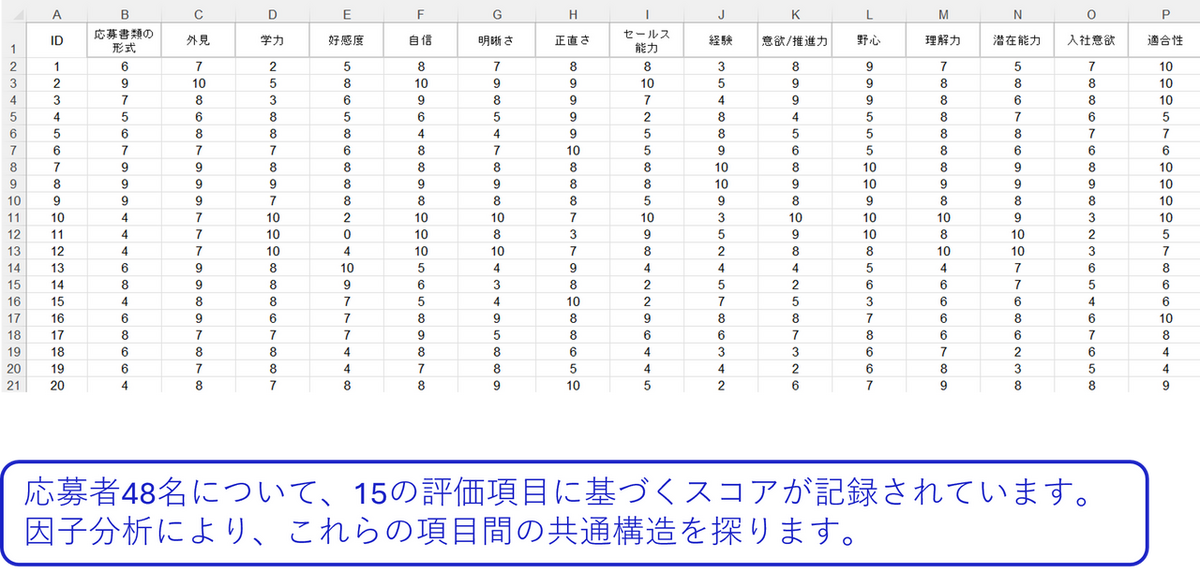
ここでは、企業の採用選考を想定したデモデータを使用します。データは、15 の評価項目に基づく48名の応募者の情報で構成されており、各項目は0～10 の11段階で評価されています。A 列には応募者のID、B～P 列には評価項目のスコアが記録されています。

このデータを用いて因子分析を行うことで、応募者の特性（能力、性格、経験など）が、どのような共通の資質や能力に集約できるのかを明らかにします。

サンプルデータのダウンロードはこちらから

Demo_FA_JP.zip

因子分析の操作手順

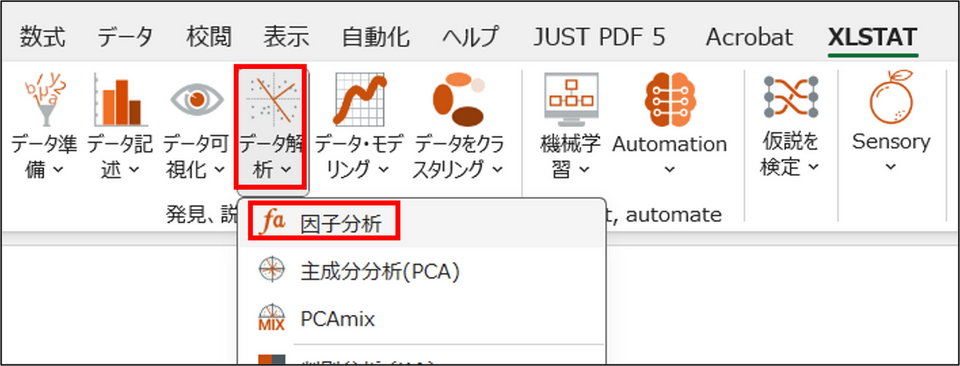
1. XLSTAT を起動し、[データ解析] > [因子分析] を選択します。

   

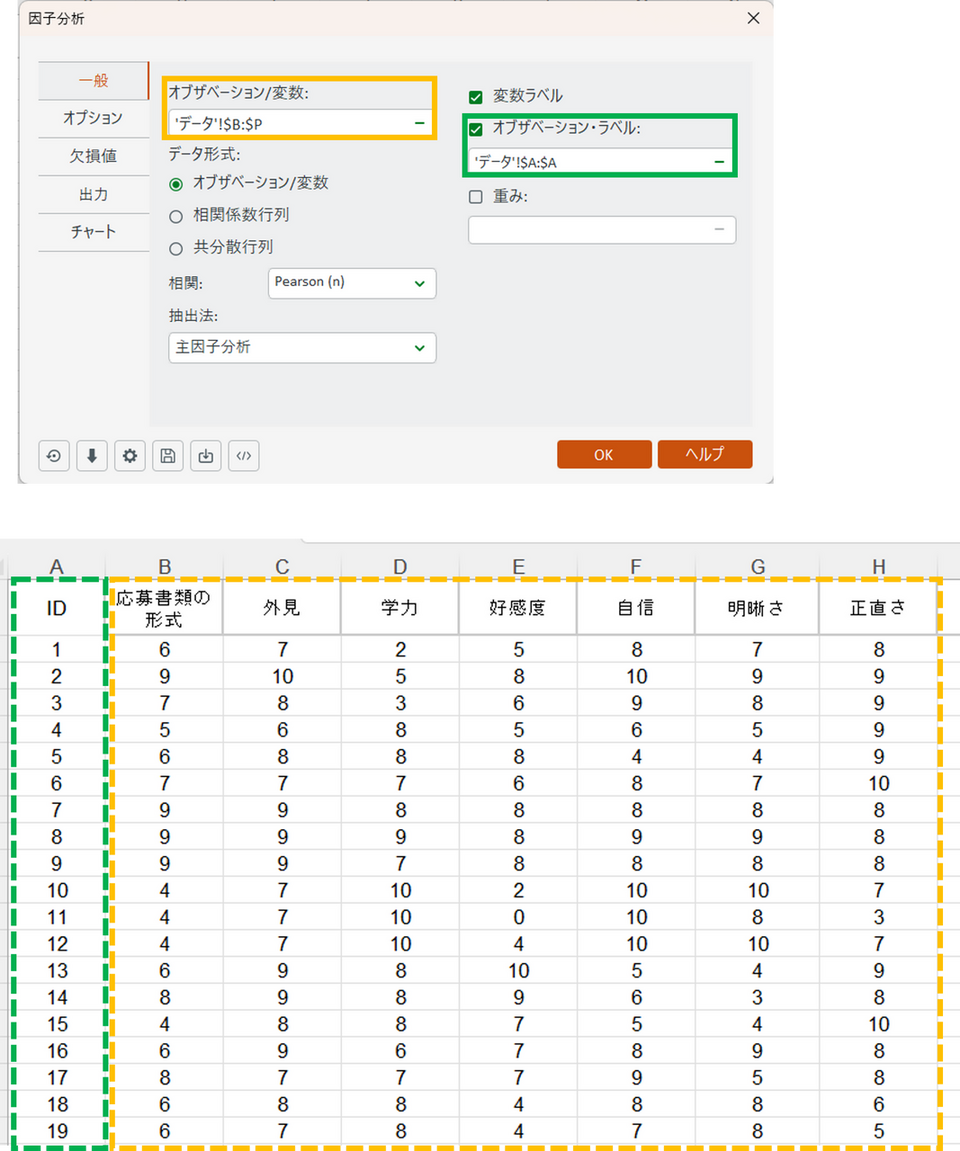
2. ダイアログボックスが表示されるので、一般タブで下記の通りデータを選択し、項目を設定します。

   

3.  [オプション] タブに切り替え、以下の項目を指定します。

   

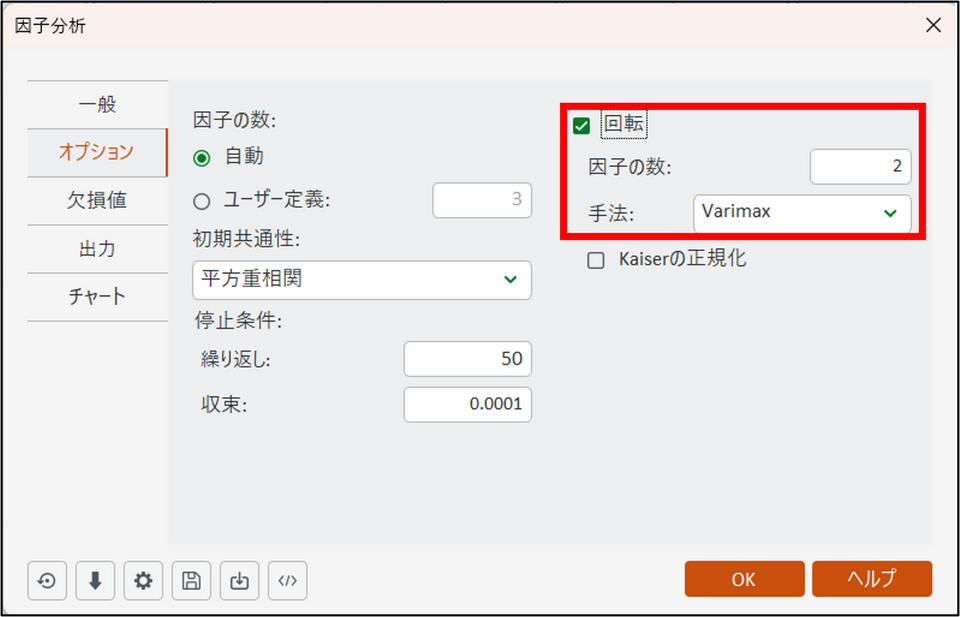
   • 回転：
     チェックを入れ、因子の数は「2」、手法は「Varimax」を選択します。

   ---

   因子分析では、共通因子をより明確に解釈できるように「軸の回転」を行います。回転によって、各変数がどの因子と強く関係しているのかがはっきりし、結果の意味がわかりやすくなります。回転方法には「直交回転」と「斜交回転」がありますが、ここでは直交回転の一種である「バリマックス回転（Varimax rotation）」を使用します。これは、因子間の独立性を保ちながら、各変数が特定の因子に強く対応するように調整する方法です。

4. [出力] タブに切り替え、[Cronbachのα係数] にチェックを入れます。

   

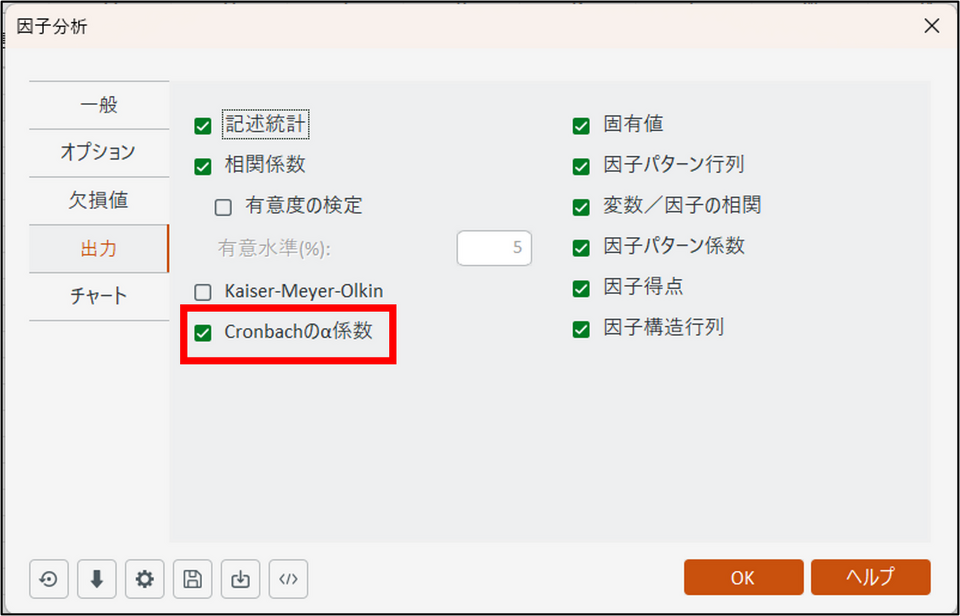
5.  [OK] をクリックすると計算が実行されます。

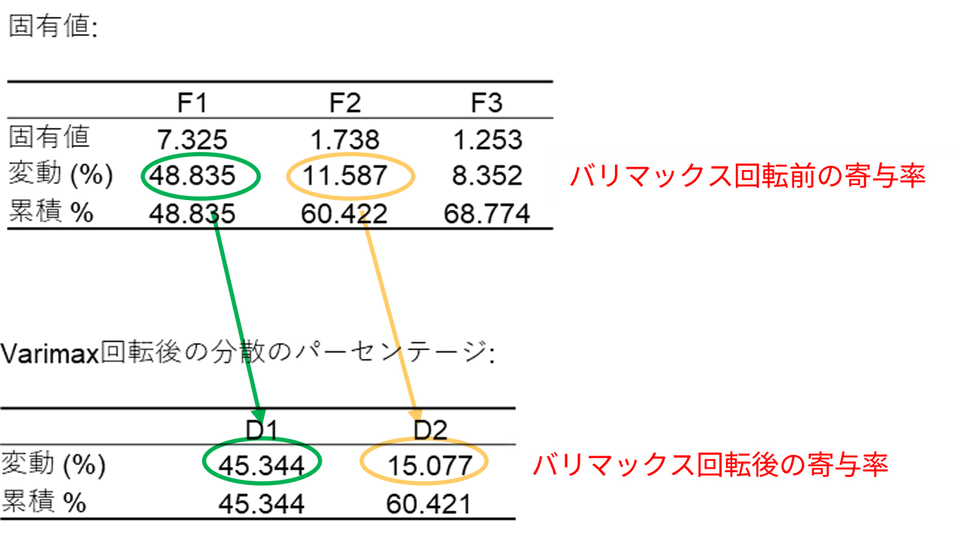
6. 計算が完了すると、各因子の寄与率（％）を示すグラフが表示されます。これは、各因子が全体の情報のうちどれだけを説明しているかを表します。ここでは、寄与率の高いF1 とF2 を選択してプロットを作成します。この2つの因子で全体の60.42% の情報をカバーしています。

   

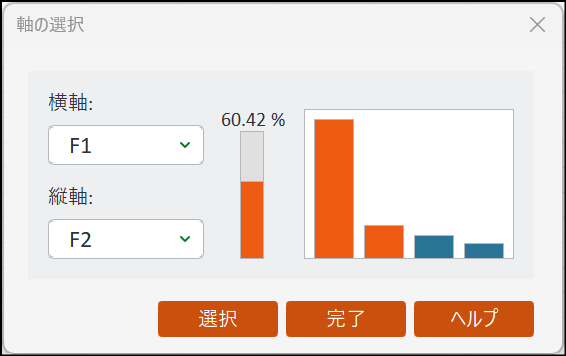
7. [完了] をクリックし、処理が完了すると結果が別シート（FAC）に出力されます。

因子分析の結果の解釈

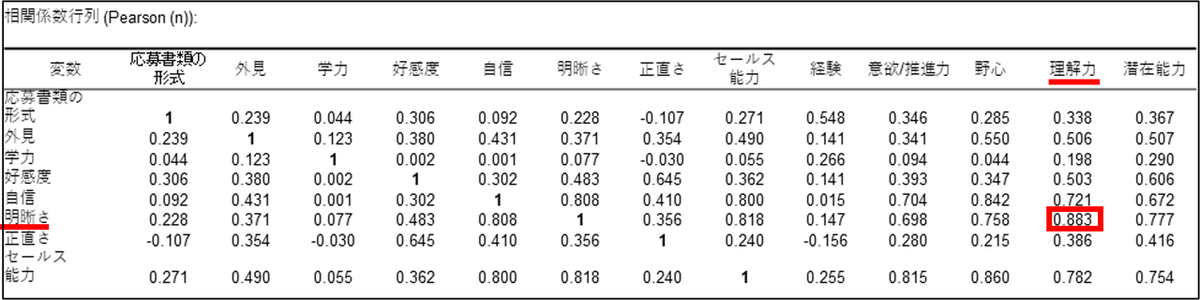
結果にはまず、各評価項目の平均値や標準偏差などの記述統計と、相関係数行列が表示されます。相関係数行列では、数値が1に近いほど2つの項目の間に強い相関があることを示します。たとえば、「明晰さ」と「理解力」の相関係数が0.883であることから、これらの項目には強い関連があることがわかります。

クロンバックのα係数

クロンバック（Cronbach）のα係数は、アンケートや評価項目（ここでは「応募書類の形式」「外見」「学力」など）が、同じ特性を測定しているかどうか、つまり一貫性があるかを確認するための指標です。この値は0から1の間をとり、一般的に0.7以上であれば信頼性が高いとされます。一方で、0.9以上と非常に高い場合は、内容が重複している、つまり似たような項目が多く含まれている可能性があります。

今回の分析では、α係数が0.914と非常に高く、評価項目の内容に冗長性がある可能性が考えられます。

固有値

固有値の結果からは、4つの因子によってデータ全体の74.5％の変動を説明できることがわかります。これは、元の複雑な情報の大部分を、4つの共通因子に集約できたことを意味します。

バリマックス回転後の結果

次に、バリマックス回転後の結果を確認します。回転を行うことで、因子の寄与率（固有値）は変化しますが、その分、因子ごとの意味が明確になり、解釈しやすくなります。

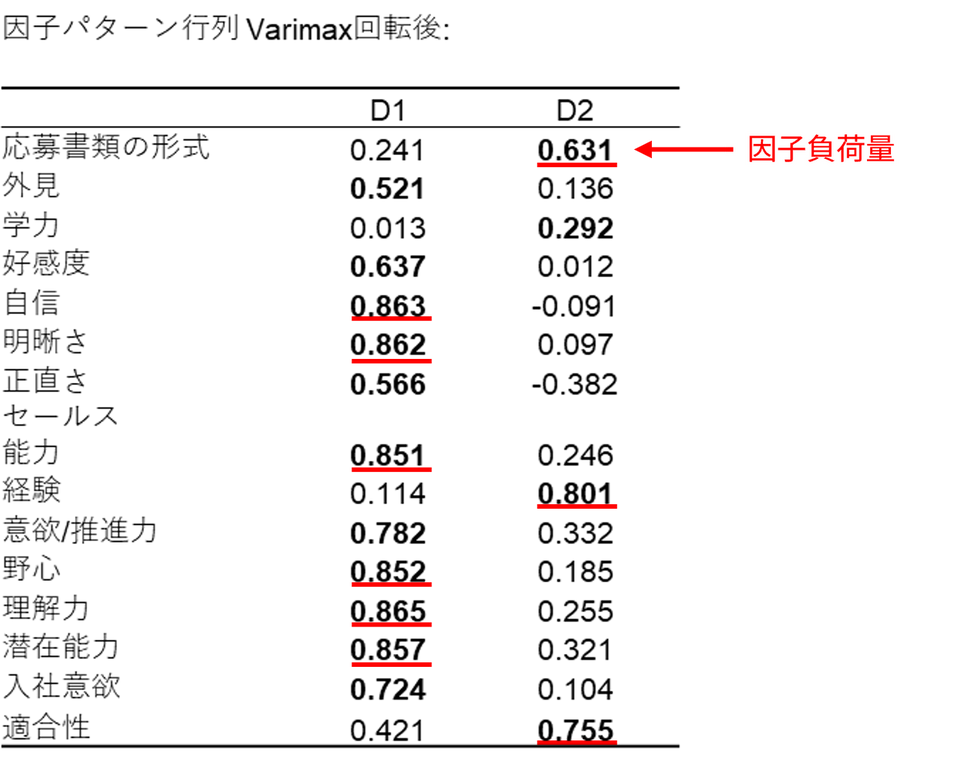
バリマックス回転後の因子パターン行列には、各評価項目がそれぞれの因子とどの程度関連しているかを示す因子負荷量が表示されます。これにより、どの変数がどの因子に強く関係しているかが一目でわかります。

例えば、第1因子（D1）は「自信」「明晰さ」「セールス能力」「野心」「理解力」といった項目と高い正の相関を持ち、これらをまとめる因子と考えられます。一方、第2因子（D2）は「応募書類の形式」「経験」「適合性」といった項目と関連しており、また異なる側面を表しています。

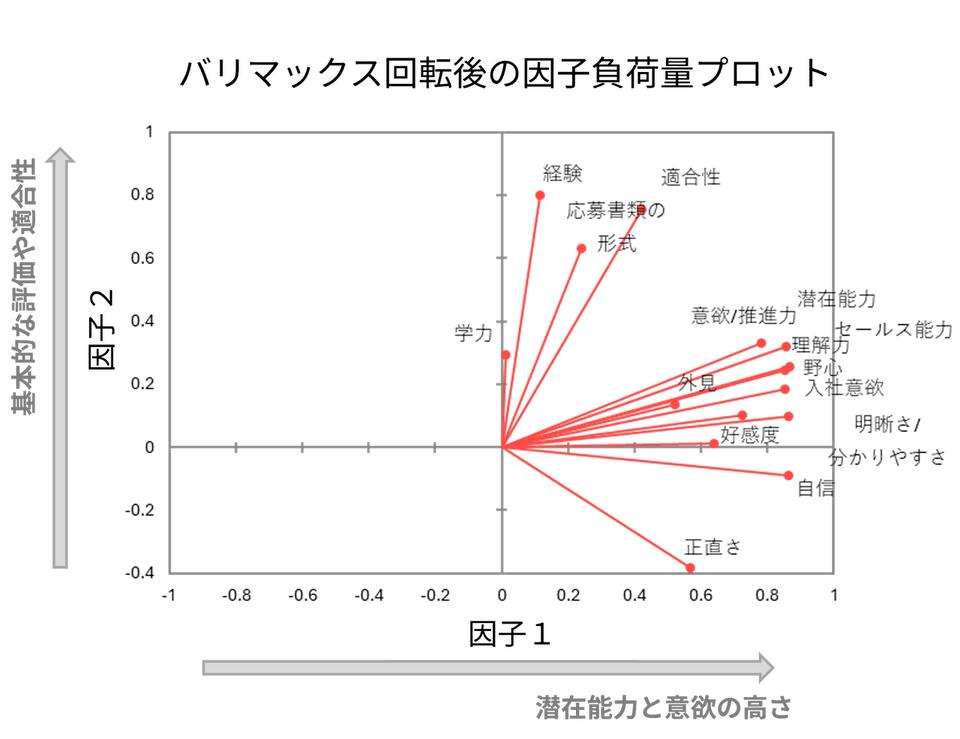
下の図は、因子分析の結果として得られた第1因子（D1）と第2因子（D2）に対する各変数の因子負荷量を二次元空間にプロットしたものです。各変数は、原点から矢印で示されており、それぞれの因子に対してどれだけ強く関係しているかが視覚的にわかります。

第1因子（D1）は、応募者の潜在的な能力や意欲の高さを表しており、この軸上で高い値を示す変数が多い応募者は、営業職などに適していると考えられます。

一方、第2因子（D2）は、基本的な評価や職務適合性に関連しており、この軸で高い値を示す応募者は、管理職などへの適性が高い可能性があります。

このように、因子軸上における変数の位置関係を確認することで、因子の性質や役割を直感的に理解することができます。

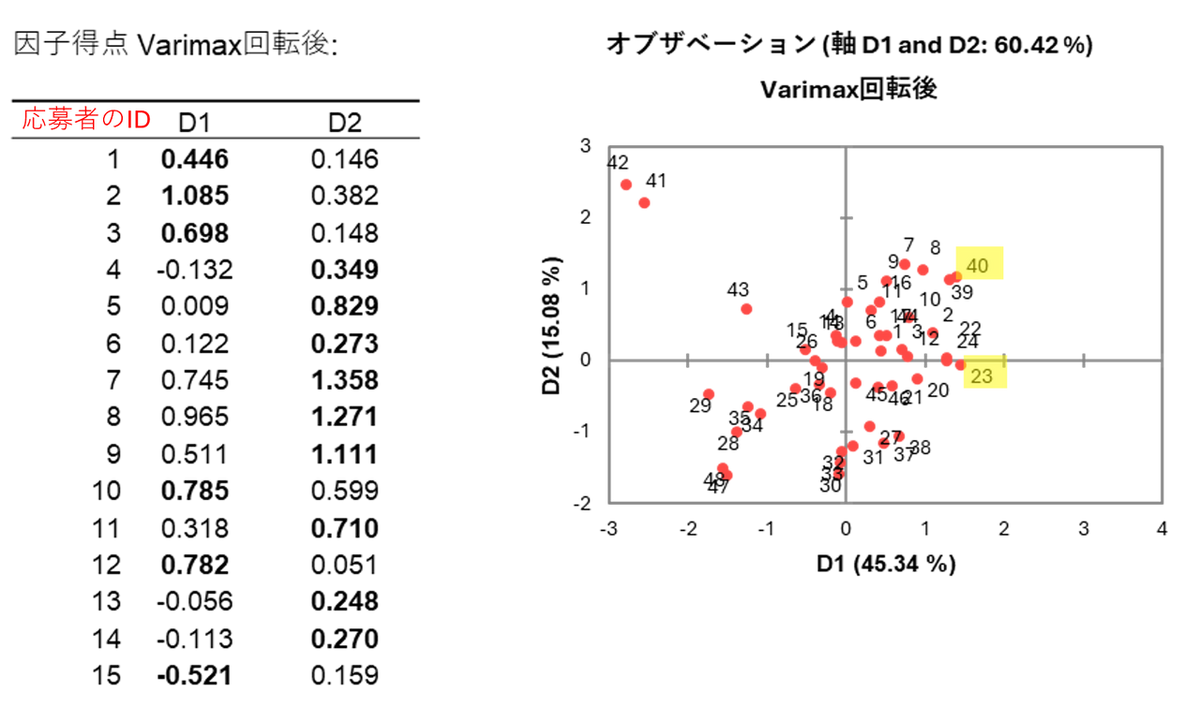
最後に、因子得点と、各個体を因子軸上に配置した2次元マップから、各個体がそれぞれの因子にどの程度関わっているかを、数値と図（グラフ）の両方で確認することができます。

例えば、グラフで見ると右上（第1象限）に位置するID40 は、第1因子・第2因子の両方の得点が高く、意欲や適合性の両面で優れていると考えられます。一方、ID23 は第1因子の得点が高く第2因子は低いため、意欲は高いものの、職務適合性の面ではやや注意が必要なタイプといえます。

まとめ

因子分析は、複雑なデータの背後にある共通の要因（因子）を明らかにするための手法です。多くの観測変数を、より少ない数の因子に整理・集約することで、データの構造をシンプルにし、全体像を把握しやすくします。これは、データに潜むパターンや傾向を見つけたいときに有効な方法であり、マーケティングや心理学、教育、品質管理など、さまざまな分野で活用されています。

補足1：抽出法と回転法

抽出法

抽出法とは、観測データからどのように因子（潜在変数）を導き出すかを決める方法です。主な手法として、主成分法、主因子法、最尤法、最小二乗法などがあります。

XLSTAT では、以下の3つの抽出法が利用可能で、主因子法がデフォルトとして設定されています：

• 主成分法：
  主成分分析でも使われる方法で、観測変数の分散を最大限に説明する主成分を抽出します。因子分析では比較用として提供されています。
  
  

• 主因子法：
  観測変数の共分散構造を説明する共通因子を抽出します。
  
  

• 最尤法：
  観測データが最もよく説明される因子構造を推定する方法です。

回転法

回転法は、抽出された因子をより解釈しやすくするために因子軸を回転させる方法です。回転には次の2種類があります：

• 直交回転：因子間の相関をゼロ（独立）と仮定して回転します。
• 斜交回転：因子間に相関があることを前提に回転します。

XLSTAT では、以下のような回転法が提供されています。

直交回転	Varimax, Quartimax, Equamax, Parsimax, Orthomax
斜交回転	Promax, Orthomax, Oblimin

一般的によく使用されるのは、直交回転のバリマックス回転（Varimax rotarion）と、斜交回転のプロマックス回転（Promax rotation）です。

回転のイメージ（単純構造）

下の図は、回転によって因子の意味が明確になる様子を表したものです。横軸に因子1、縦軸に因子2を取った2次元空間に、各変数をプロットしています。
回転前の状態では、ほとんどの変数が因子1と因子2の両方から影響を受けており、それぞれの因子の意味を解釈しにくくなっています。
しかし、因子の軸を回転させることで、因子1の影響が強い変数群と、因子2の影響が強い変数群が明確に分かれ、「単純構造」に近づくため、因子の解釈が格段にしやすくなります。

補足2：用語の説明

因子負荷量：

各変数が、因子からどの程度の影響を受けているかを示す数値です。一般的に、この数値が高い変数を手がかりにして、因子に意味づけ（命名）を行います。因子負荷量を一覧にまとめたものが「因子パターン行列」です。

独自因子：

各変数に特有のばらつきを指します。これは共通因子では説明できない部分であり、測定誤差や個別の特徴などが含まれます。

因子得点：

各個体（調査対象者）が、各因子にどの程度関わっているかを数値で表したものです。因子得点が高いほど、その因子の特徴を強く持っていると解釈されます。

補足3：主成分分析と因子分析の違い

主成分分析

• 目的：データのばらつきをできるだけ失わずに要約すること
• 元のすべての変数の情報を、少数の「主成分」に圧縮して表現します。
• 各主成分は、変数の分散を最大限に保持するように構成され、すべてのばらつきを説明することが前提です。

因子分析

• 目的：複数の変数の背後にある共通の構造（＝因子）を見つけること
• 各変数に含まれるばらつきを、「共通因子が説明する部分（共通性）」と「それ以外の部分（独自性）」に分けて考えます。
• 全てのばらつきを因子で説明する必要はなく、共通の要因だけに注目するのが特徴です。

参考文献

• XLSTAT: Factor Analysis in Excel
  https://community.lumivero.com/s/article/6608-factor-analysis-excel-tutorial?language=en_US
  
  
• 涌井良幸,  涌井貞美：多変量解析がわかる,  技術評論社, 2011.
  
  
• 日本官能評価学会 編, 必読官能評価士認定テキスト, 霞出版社, 2020.

XLSTAT の無料トライアル

トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した因子分析はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。