XLSTAT による主成分分析:アメリカ51州の人口変動から地域別の特徴と傾向を探る
記事執筆:一般社団法人学術・教育総合支援機構 倉山 太一、川﨑 洋平
一般社団法人学術・教育総合支援機構公式HP:https://iaae.jp/
- 主成分分析とは?
- 主成分分析を実行をするためのデータセット
- XLSTAT を用いた主成分分析の手順
- 主成分分析の結果の解釈
- 主成分分析の利用に関する備考
- 主成分分析への補助変数の追加
- 主成分分析実行後の凝集型階層的クラスタリング(AHC)の実行
- まとめ
- 参考文献
- XLSTAT の無料トライアル
主成分分析とは?
主成分分析は、多数の変数を持つデータを、より少ない指標や合成変数(主成分)に要約する統計学的な分析手法です。この主成分分析を歩行中の筋肉活動を例にとって考えてみましょう。人間は歩行中に全身の筋肉を使います。実際に歩行中の筋肉の活動を観察すると、それぞれの筋肉がバラバラのパターンで活動しており、一見してその特徴はわかりません。しかし、我々が知りたいのは、「歩行に特徴的な筋活動パターンは何か?」であったとします。このような場面で主成分分析は役に立ちます。実際に、主成分分析を用いた研究によると、一見複雑に見える人間の歩行筋活動はたった5つのパターンでその90%以上が説明できることが知られています。つまり、主成分分析は「ある観測値が、たくさんある変数のうちどの変数によって主に説明されるのか?」といったことを知ることができます。このページでは、XLSTAT を使用して主成分分析を行う方法と、その解釈の仕方を説明します。
主成分分析を実行をするためのデータセット
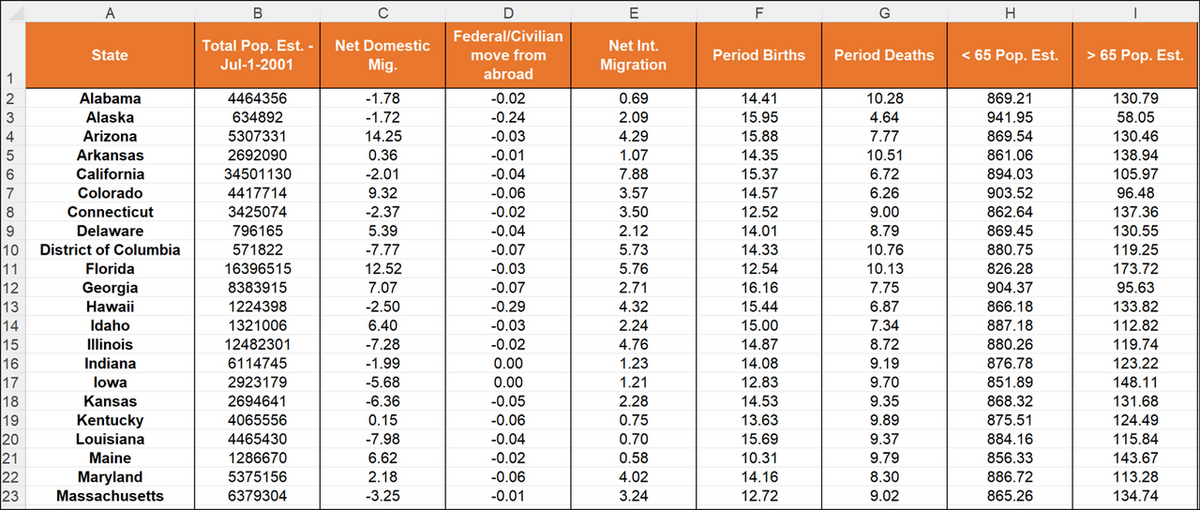
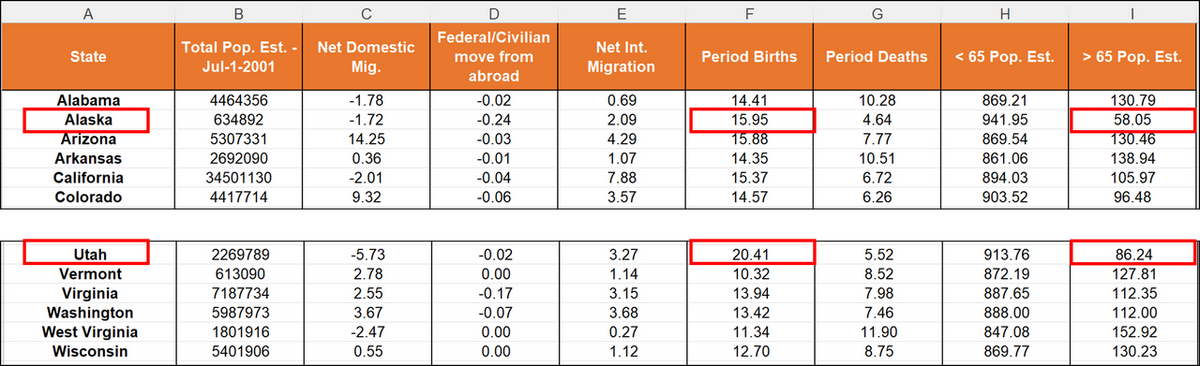
このページで使用するデータは米国国勢調査局によるもので、2000年から2001年にかけての51州の人口変化を表しています。最初のデータセットは、人口1,000人当たりの割合に変換され、2001年のデータが分析の対象となります。今回はこのデータで主成分分析を行い、変数間の相関を分析し、ある州における人口の変化が他の州における変化と大きく異なるかについて調べてみます。
サンプルデータのダウンロードはこちらから
demo_PCA_EN.xlsXLSTAT を用いた主成分分析の手順
-
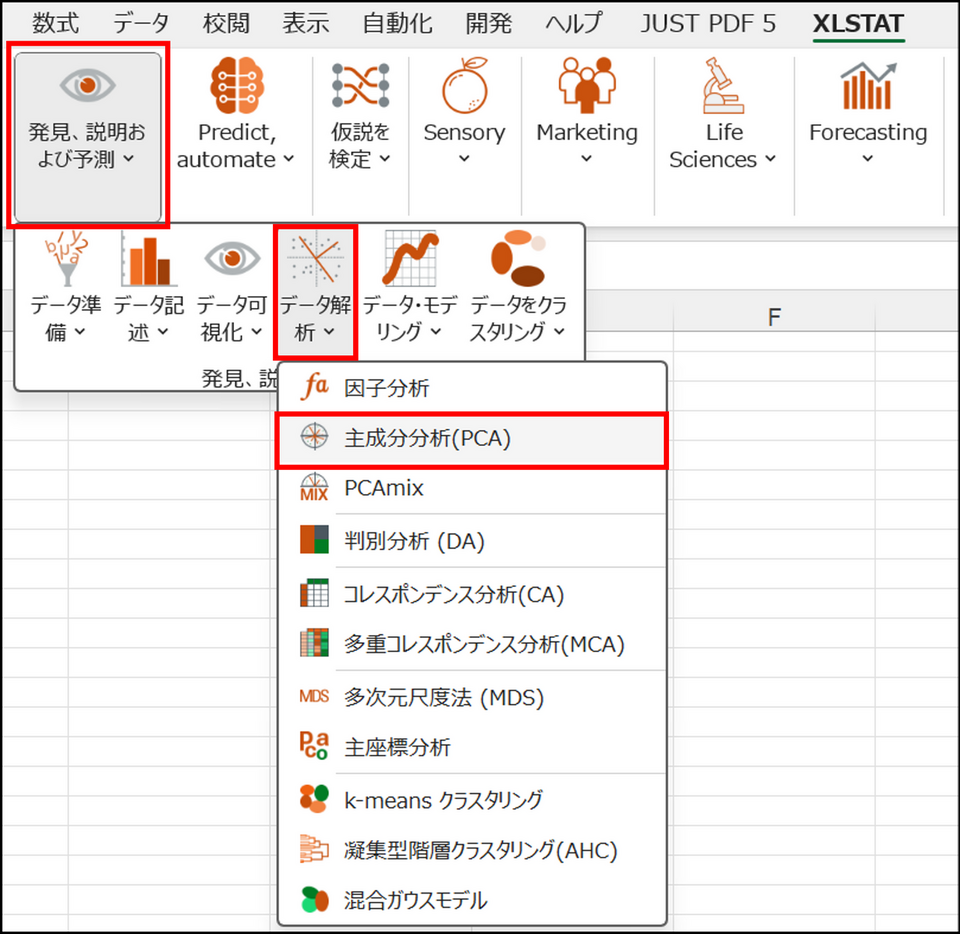
XLSTAT を起動し、[発見、説明、および予測] > [データ解析] > [主成分分析(PCA)] を選択します。
-
ダイアログボックスが表示されるので、下記項目を指定します。
- [オブザベーション/変数]:
分析対象の変数データが記録されているセルを選択します。データの選択は入力欄にカーソルを置き、その後でエクセル上のデータを直接指定することで可能です。今回は列名も含めて選択します。 - [オブザベーション・ラベル]:
分析対象の変数ラベルが記録されているセルを選択します。今回の場合は、州の名前が入力されているA列を選択します。 - [PCAタイプ]:
[相関 (Pearson)] を選択 します。これにより計算中に使用されるPCA タイプは、ピアソン相関係数に対応する相関行列になります。共分散行列は、より高い分散を持つ変数により多くの重みを割り当てます。異なる分布の変数で主成分分析を実行する場合は、[相関 (Spearman)] の相関のほうがより適切な場合があります。
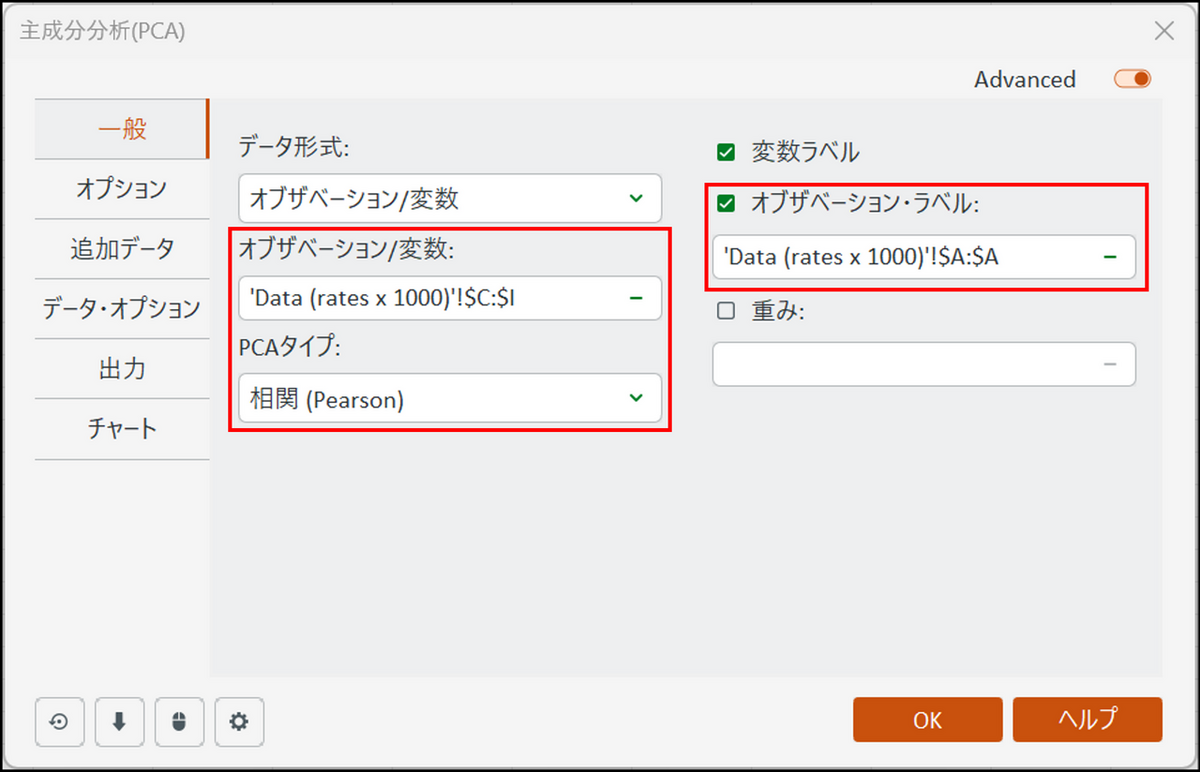
- [オブザベーション/変数]:
-
[出力] タブに切り替え、[相関係数] と [有意度の検定] にチェックを入れておきます。
[有意度の検定] にチェックを入れることにより、出力結果の相関表で有意な相関を太字で表示します。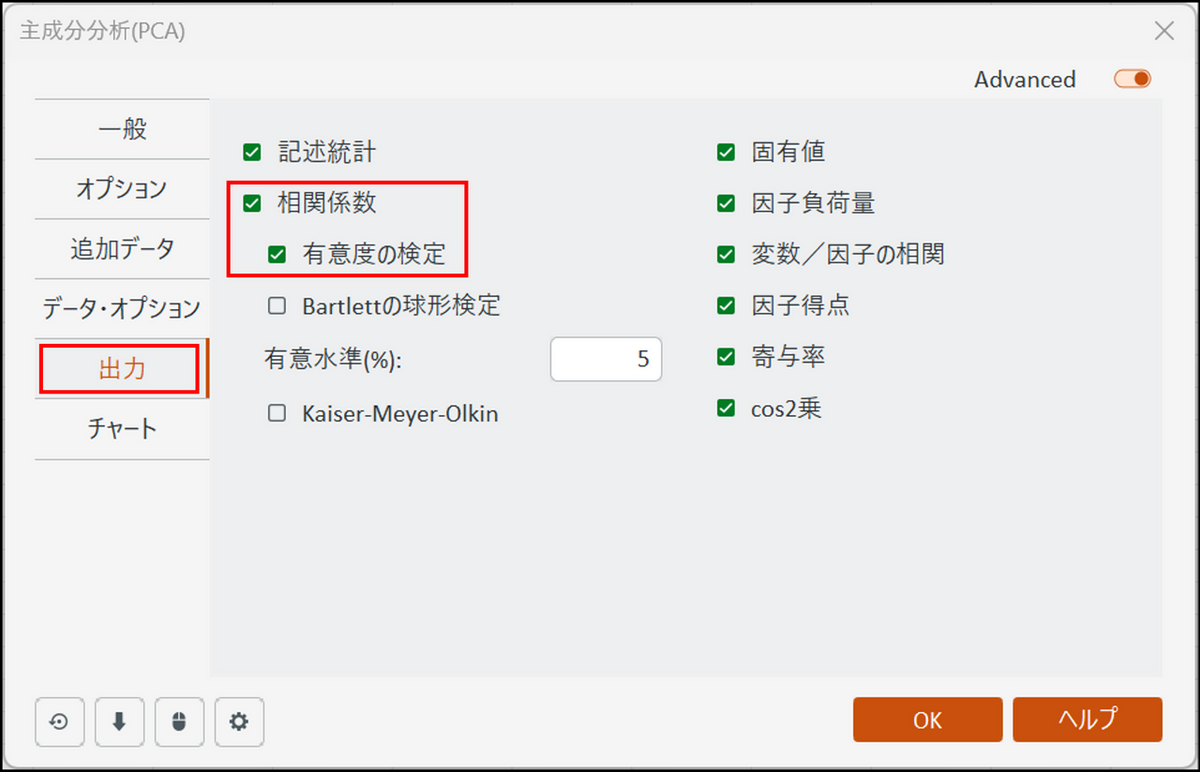
-
[OK] ボタンをクリックすると、計算が実行されます。
-
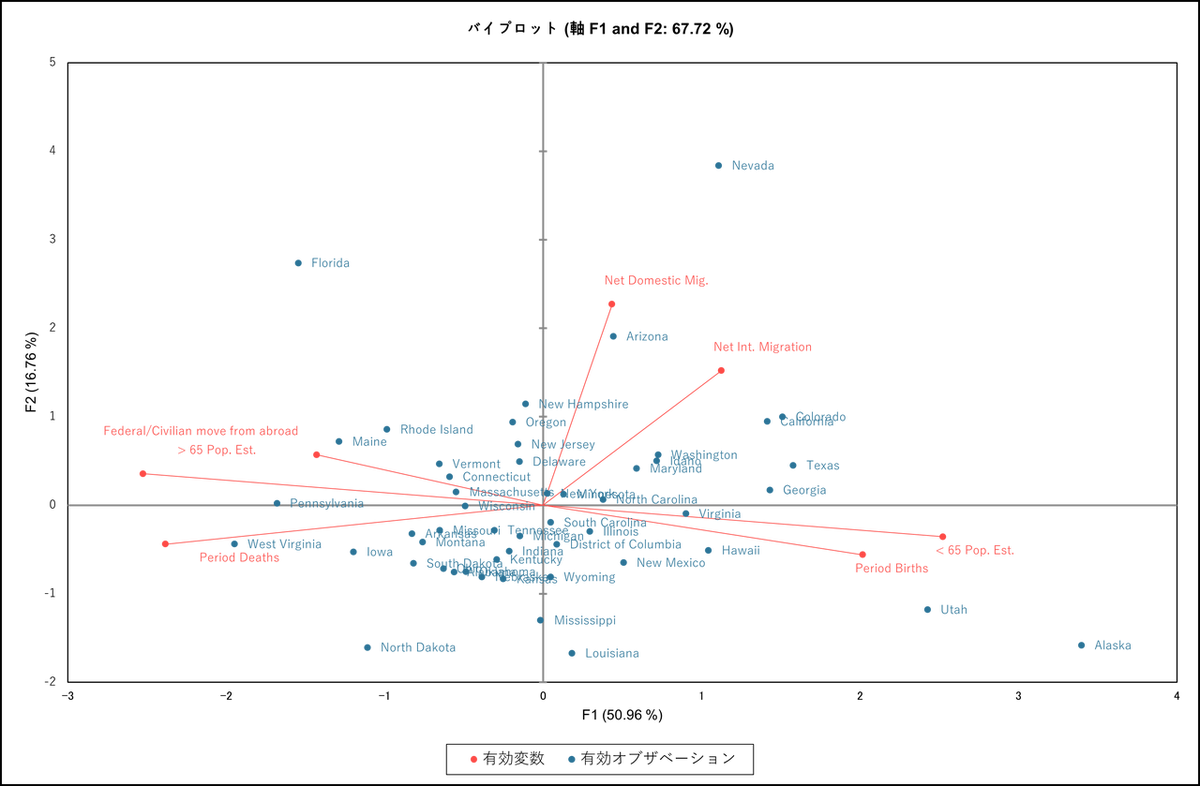
計算が終了すると変動(%)を表すグラフが表示されるので、プロット表示したい軸を選択します。変動(%)とは各主成分が持つ情報の割合を意味します。今回の事例では、最初の2つの主成分(F1 と F2)によって表現される分散の変動は67.72% です。つまり、F1 と F2 でデータセット全体の67.72% の情報を担っているということになります。
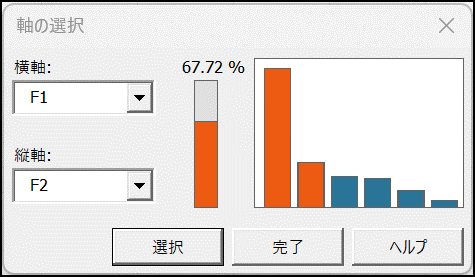
横軸または縦軸で別の主成分を選択すると、変動(%)が変化することを確認できます。
-
今回は情報が最も多く含まれるF1 と F2 を選択した状態で主成分分析を実行します。[横軸] にF1、[縦軸] にF2 を選択し、[完了] をクリックします。処理が完了すると、結果が別シート(PCA)に出力されます。
主成分分析の結果の解釈
主成分分析の結果には、様々な表やグラフが出力されますが、各項目で見るべきポイントは以下の通りです。
相関行列:
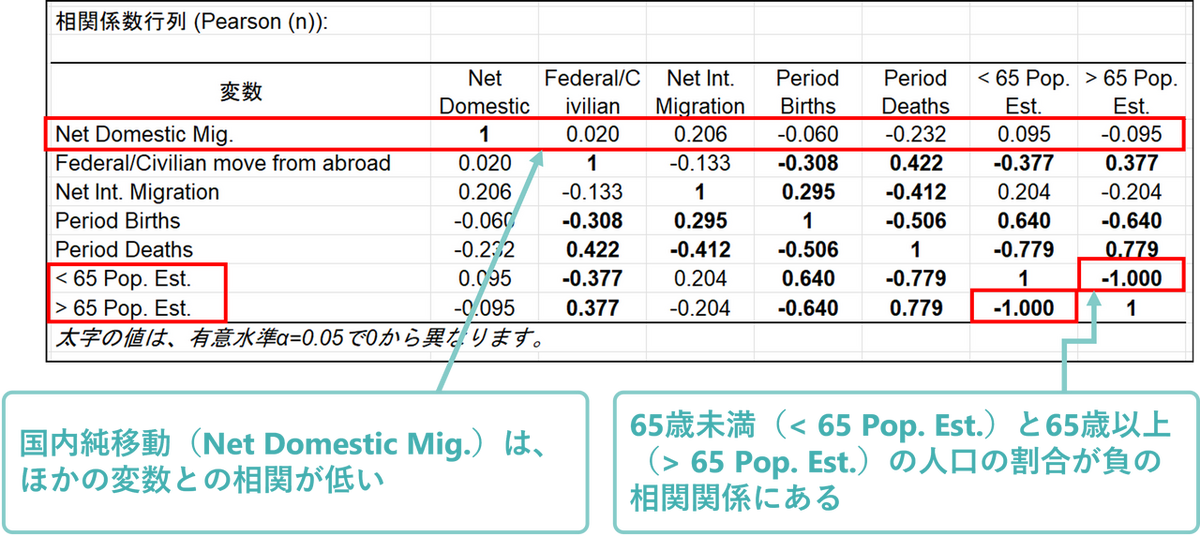
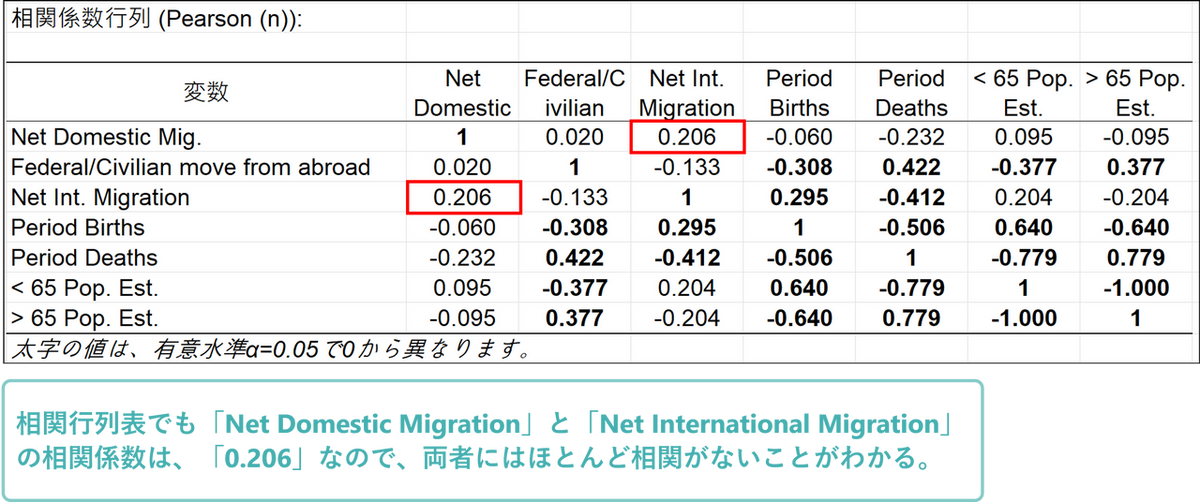
最初に見るべき結果は相関行列です。相関行列を確認すると、65歳未満(< 65 Pop. Est.)と65歳以上(> 65 Pop. Est.)の人口の割合が負の相関関係にあることがすぐにわかります(r = -1)。つまり、どちらかの変数を削除しても、分析結果に大きな影響はありません。また、国内純移動(Net Domestic Mig.)は、国際純移動(Net Int. Migration)を含む他の変数との相関が低くなっています。これは、米国人と非米国人では、移住の理由が異なる可能性を示唆しています。
固有値:
次に、固有値の表とグラフを確認します。固有値とは各主成分が含んでいる情報の大きさを示す指標です。固有値が大きいほど、その主成分は多くの情報を説明していることになります。この例では、最初の固有値(F1)が3.567 であり、全変動の約51%を表していることがわかります。つまり、この1つの軸だけでデータを表現した場合でも、データ全体の変動の51%を把握することが可能であることを意味します。
各固有値は因子に対応し、各因子は1つの次元に対応します。因子は、初期変数の線形結合で、すべての因子は互いに相関関係がありません(r=0)。固有値と対応する因子は、それらが初期変動のどれだけの量を表すか(%に変換)の降順でソートされます。大まかに言うと、因子 = PCA 次元 = PCA 軸となります。
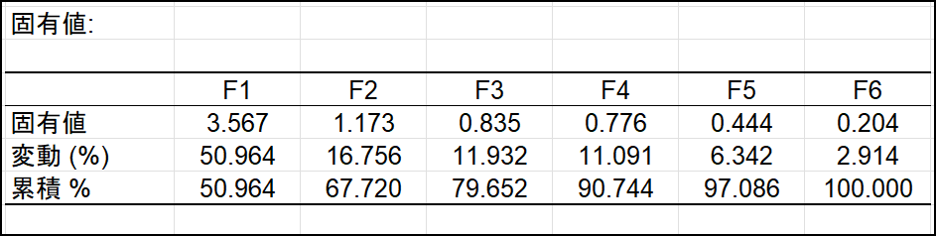
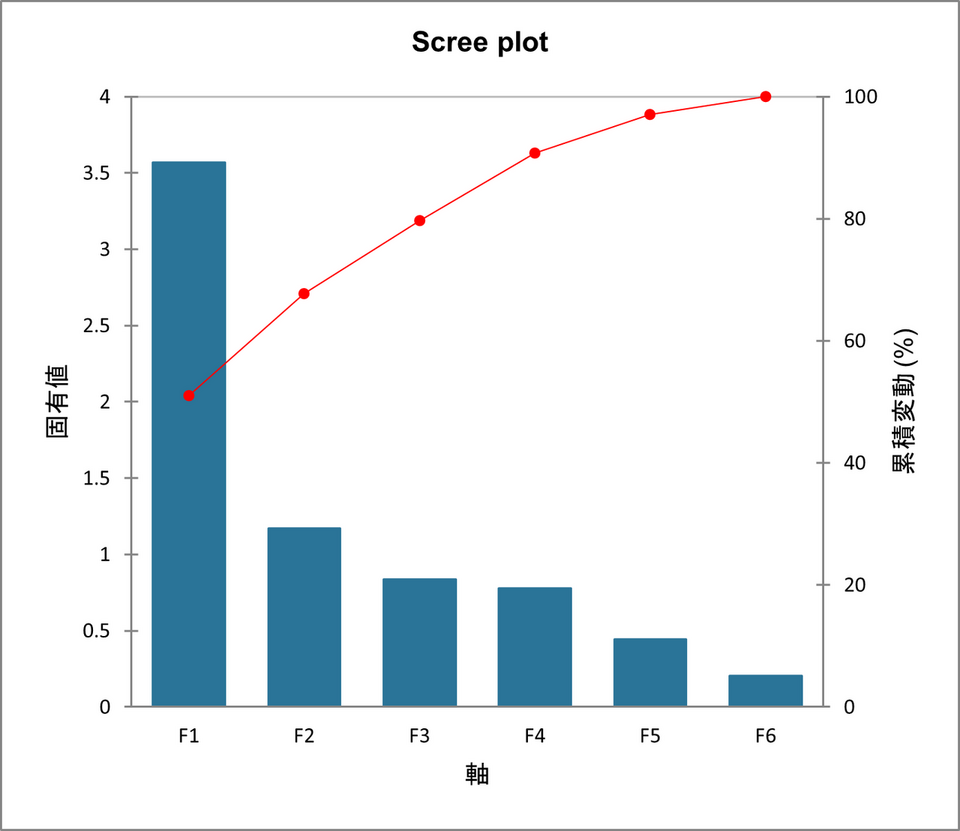
理想的には最初の2つか3つの固有値の分散の変動(%)が高ければ良質な解析結果とされています。今回の例では、最初の2つの因子によって、データの初期変動の67.72%を表現できます。これはよい結果ですが、マップを解釈するときには、次の因子に隠されている情報があるかもしれないので、注意しなければなりません。今回の例では、元のデータに7つの変数がありましたが、分析の結果、提示された因子の数は6つしかありません。これは、負の相関(r=-1)を持つ2つの年齢に関する変数によるものです。互いに逆の傾向を示す変数は、本質的には 1 つの変数で表すことができます。例えば子供の身長が伸びると、相対的な服のサイズは小さくなります。これは互いに逆の動き(r=-1)をしているように見えますが、実際は「成長」という一つの因子によって起きている事象です。このような変数は自動的にまとめられます。
相関円:
次のグラフは、「相関円」と呼ばれるもので、軸F1と軸F2上に各変数がどのように投影されているかを示しています。主成分を軸にとった座標で、第一主成分であるF1(factor 1)を横軸、第二主成分であるF2(Factor 2)を縦軸としています。この座標にそれぞれの変数(この例の場合、年齢や人口変動)を矢印でプロットし、主成分空間で見た時の、各変数の関係性を視覚化しています。
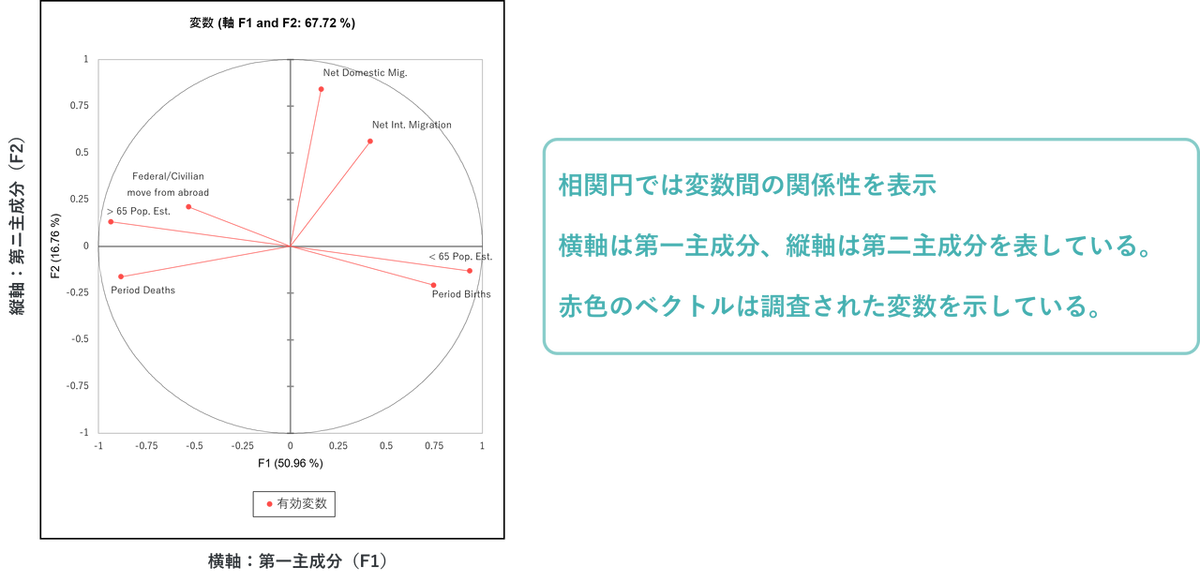
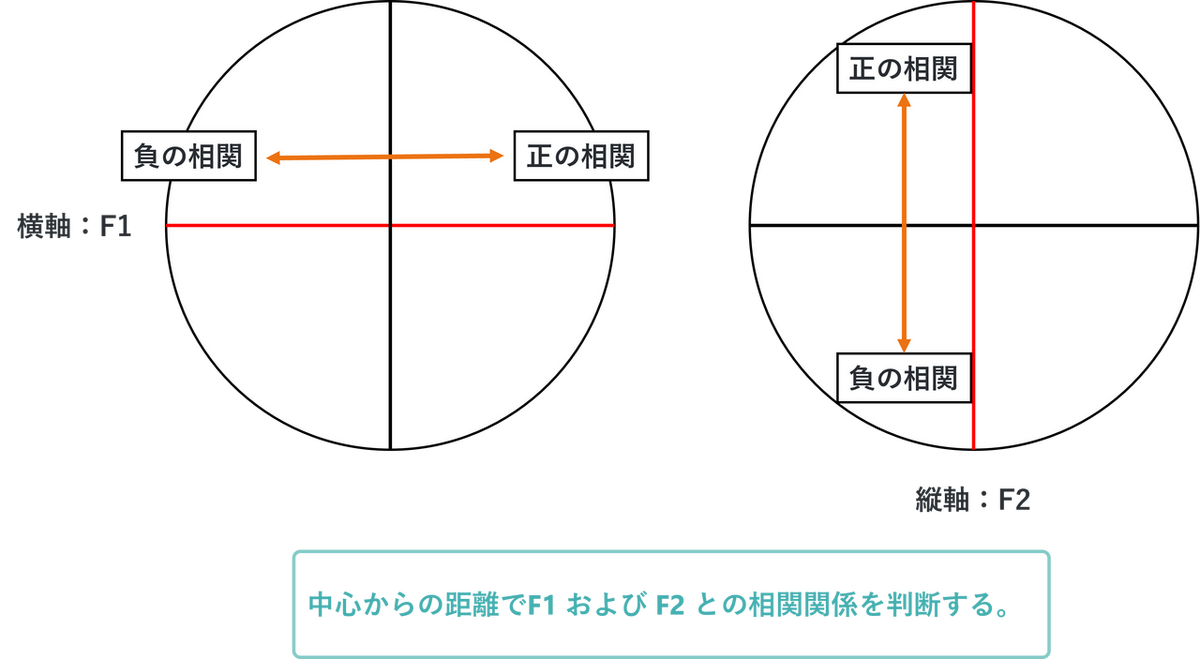
この図における解釈として、まずは矢印の距離を確認します。矢印が円の中心から遠くに伸びている場合、その変数は因子(F1/F2)と強い関連があります。左右の横軸方向に長く伸びていれば、F1 との関連が強く、上下の縦軸方向に長く伸びていればF2 との関連が強いことを示しています。また、下記の図のように伸びている方向により正負どちらの相関があるのかを判断することができます。
今回の事例で確認すると、左右の距離では下記4つの変数が中心から遠くに離れており、F1 と強い関連があることがわかります。
- < 65 Pop. Est.
- Period Births
- > 65 Pop. Est
- Period Deaths
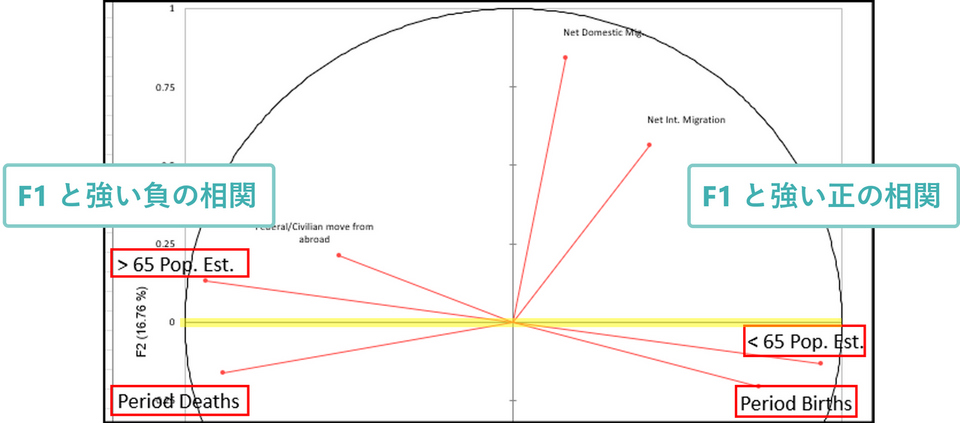
同様に上下の縦軸方向では、「Net Domestic Mig.」が上側に長く伸びているため、F2 と強い正の相関があることがわかります。
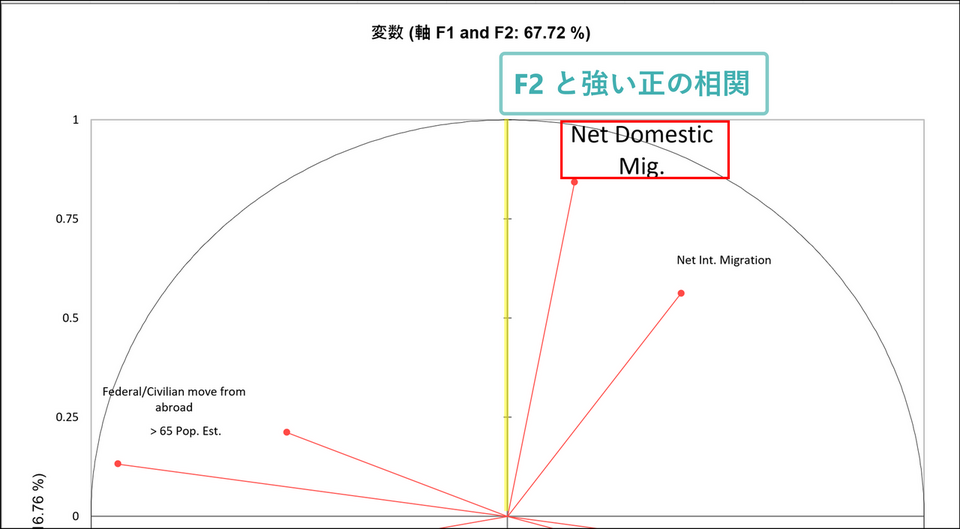
相関円は軸の意味を解釈するのにも役立ちます。今回の例では、横軸(F1)は年齢と人口変動、縦軸(F2)は国内移動と関連していると判断できます。
また、以下のようにベクトル間の角度で変数同士の相関を判断できます。
- 角度が狭い場合:変数同士に正の相関がある
- 角度が90度の場合:変数同士に相関がない
- 180度に近い場合:変数同士に負の相関がある
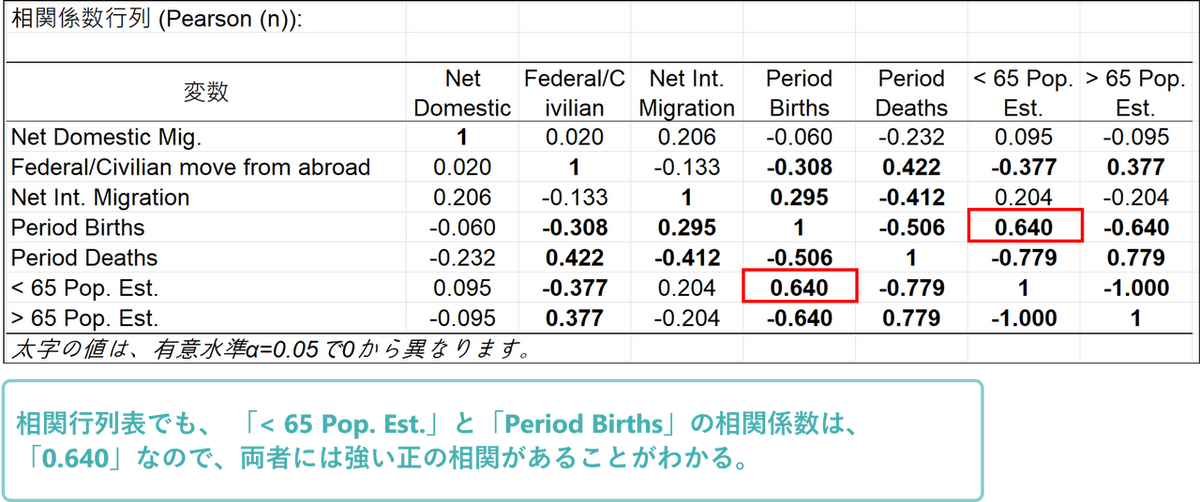
今回の例では、「< 65 Pop. Est.」と「Period Births」はベクトル間の角度が狭いので、正の相関があることが確認できます。
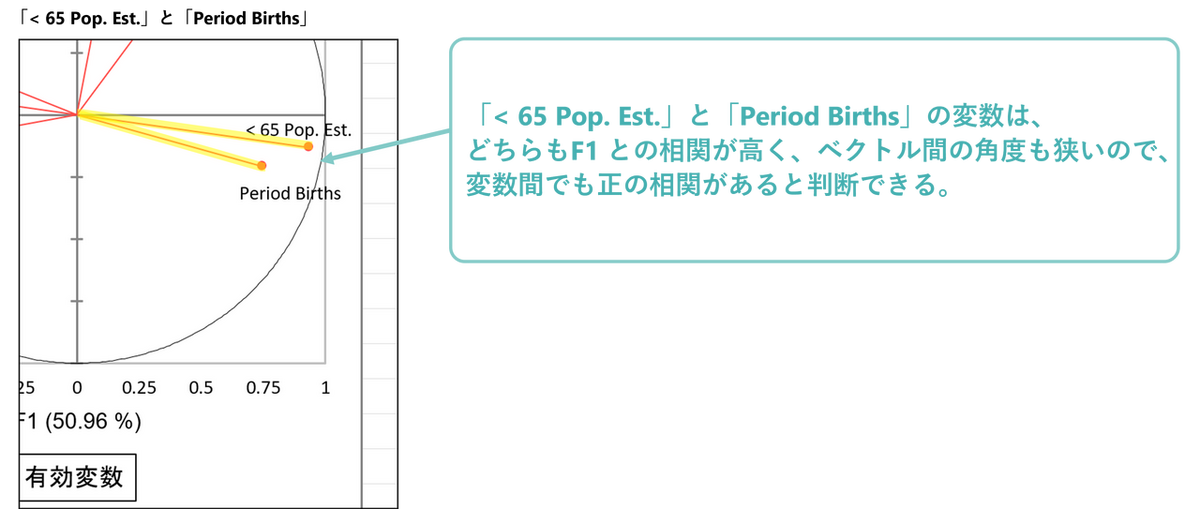
相関行列表でも両者の相関係数は「0.640」なので、強い正の相関があると判断できます。
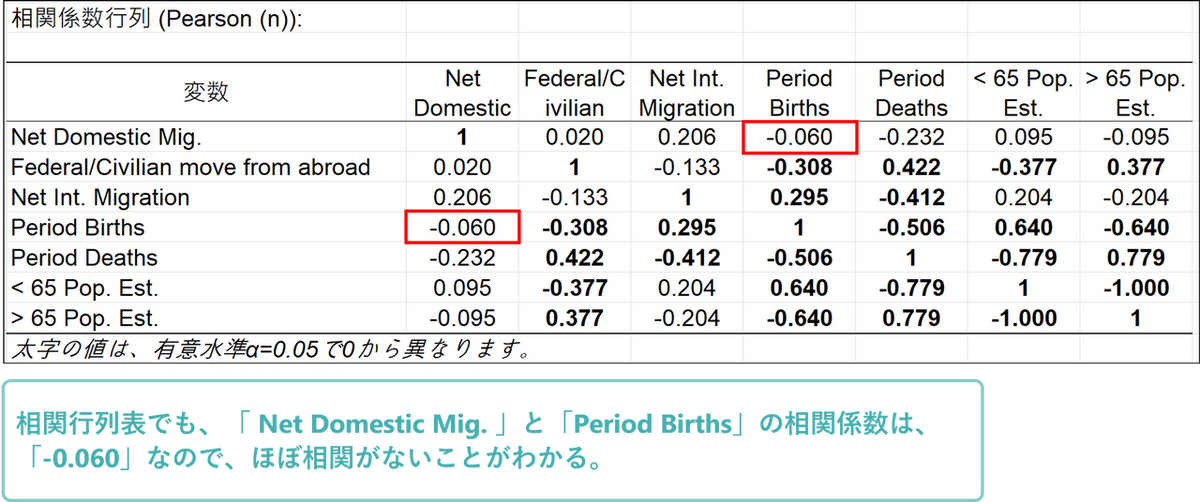
また、「Net Domestic Mig.」と「Period Biths」ではベクトル間の角度がほぼ直角なので、相関がないことが確認できます。

相関行列表でも両者の相関係数は「-0.060」なので、相関がないと判断できます。
「> 65 Pop. Est.」と「< 65 Pop. Est.」は、円上で反対の位置にあり、ベクトル間の角度が180度なので、負の相関関係にあることが確認できます。
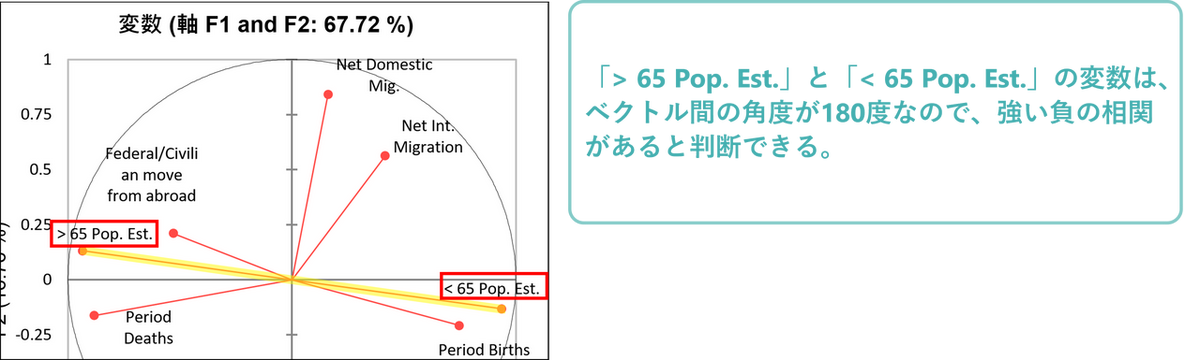
なお、変数のベクトルが短い、すなわち円の中心に近いときは、その変数は現在の空間(F1/F2)とは関連がなく、他の主成分方向に伸びている可能性があるため、解釈には注意が必要です。例えば、「Net Domestic Migration」と「Net International Migration」の矢印は同じ方向を向いており、一見すると相関関係があるように見えますが、実際には相関はありません。

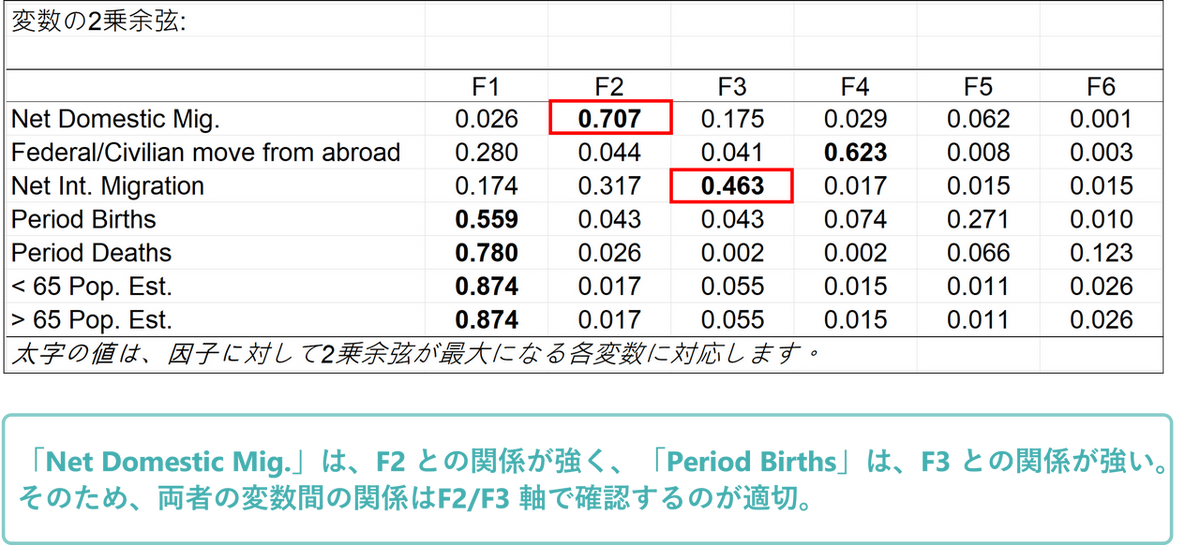
このような場合は、次の「2乗余弦」の表で各変数とより関連のある軸を確認し、別の軸で主成分分析を再実行することで適切な結果を得ることができます。
2乗余弦表:
2乗余弦の表を見ることで各変数が軸とうまくリンクしているかを確認することができます。2乗余弦が大きいほど、対応する軸との関連が大きいことを示します。与えられた変数の2乗余弦がゼロに近ければ近いほど、対応する軸の観点から結果を解釈する際は注意が必要です。この表を見ると、国際移住(「Net Domestic Migration」と「Net International Migration」)の傾向はF2/F3の軸で見るのが最適であることがわかります。
観測値:
次のグラフは、各州が2次元マップ上にどのように配置されているかを示しています。このグラフから州ごとに異なる特徴や傾向を見つけることができます。今回の例ではネバダ州とフロリダ州はほかの州とは異なる特徴を持っており、ユタ州とアラスカ州は共通の特徴を有していることがわかります。
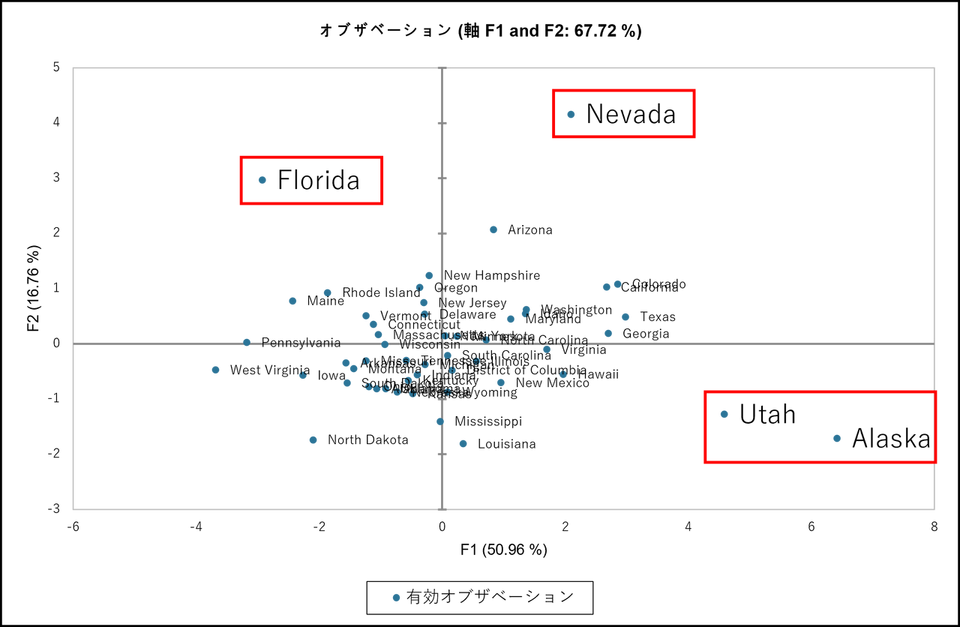
データセットによると、ユタ州とアラスカ州は65歳以上の人口比率が低いことが確認できます。また、ユタ州は全米で最も出生率が高く、アラスカ州も上位にランクされています。
バイプロット:
バイプロットでは主成分空間での変数プロットと観測値プロットを重ね合わせて表示しています。
主成分分析の利用に関する備考
主成分分析は、データ分析において様々な場面で用いられます。以下はその2つの例です。
- 回帰分析:
回帰分析では相関関係を持つ変数を使うと、分析結果が歪んでしまうおそれがあります。主成分分析を用いて変数を新しい変数に変換することで、相関の影響を排除し、より正確な分析が可能になります。 - クラスタリング:
データをいくつかのグループに分類するクラスタリングにおいては、データの次元が高いと、どの変数に基づいて分類すれば良いのか判断が難しくなります。主成分分析を用いてデータを低次元に圧縮することで、データの全体像を把握しやすくし、適切な変数を選択することができます。また、クラスタリングでは、マップ (主成分分析の結果可視化された図) を基に、単純にクラスの数を推測することもあります。
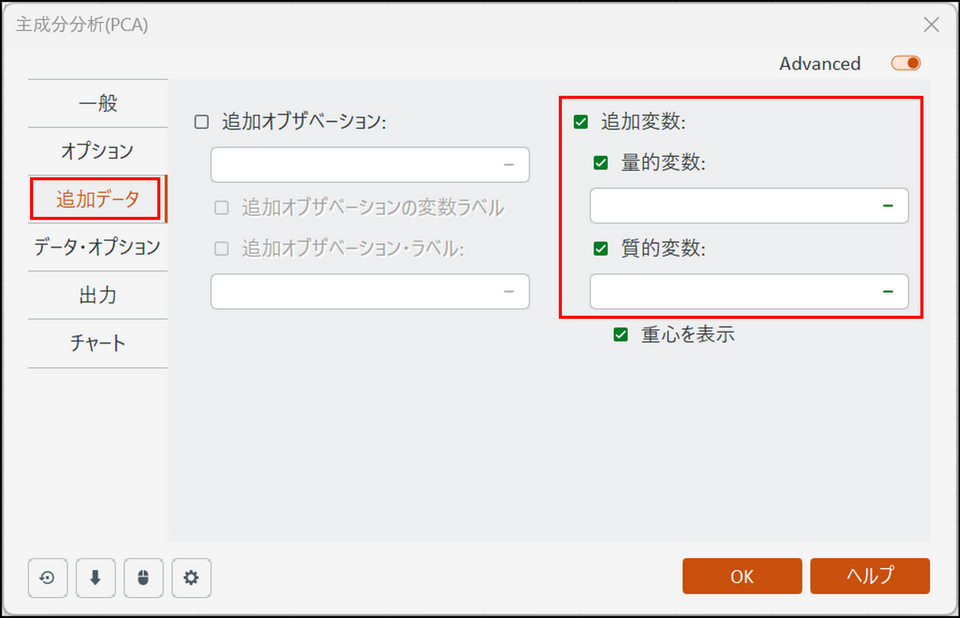
主成分分析への補助変数の追加
主成分分析を実行した後に、補助変数を追加することも可能です。これは解釈の質を高めるのに役立つ可能性があります。XLSTATでは、それらの変数は、ダイアログボックスの[追加データ] タブで選択できます。補足変数は、2つのタイプに分けられます。
- 質的補足変数:
観測値をカテゴリ別にマップ上で色分けできます。このチュートリアルの例では、各州が共和党寄りか民主党寄りかを定義する列を追加することが可能です。 - 量的補足変数:
これらの変数が主成分分析を構築するために使用された変数群とどのように相関するかについて、検討のために追加できます。主成分分析が回帰分析の前に実行される場合は、説明変数は主成分分析を構築するために使用でき、従属変数は補助変数として追加できます。これにより、どの説明変数が従属変数に最も強い影響を及ぼすのかを大まかに把握することができます。
主成分分析実行後の凝集型階層的クラスタリング(AHC)の実行
因子スコア表の下のボタンをクリックして、凝集型階層的クラスタリングを実行することもできます。オレンジ色の矢印は、多くの変数を含む場合、表の最後に直接ジャンプすることができます。
このボタンをクリックすると、ダイアログボックスが自動的に開きます。凝集型階層的クラスタリングを実行するにはOK ボタンをクリックします。
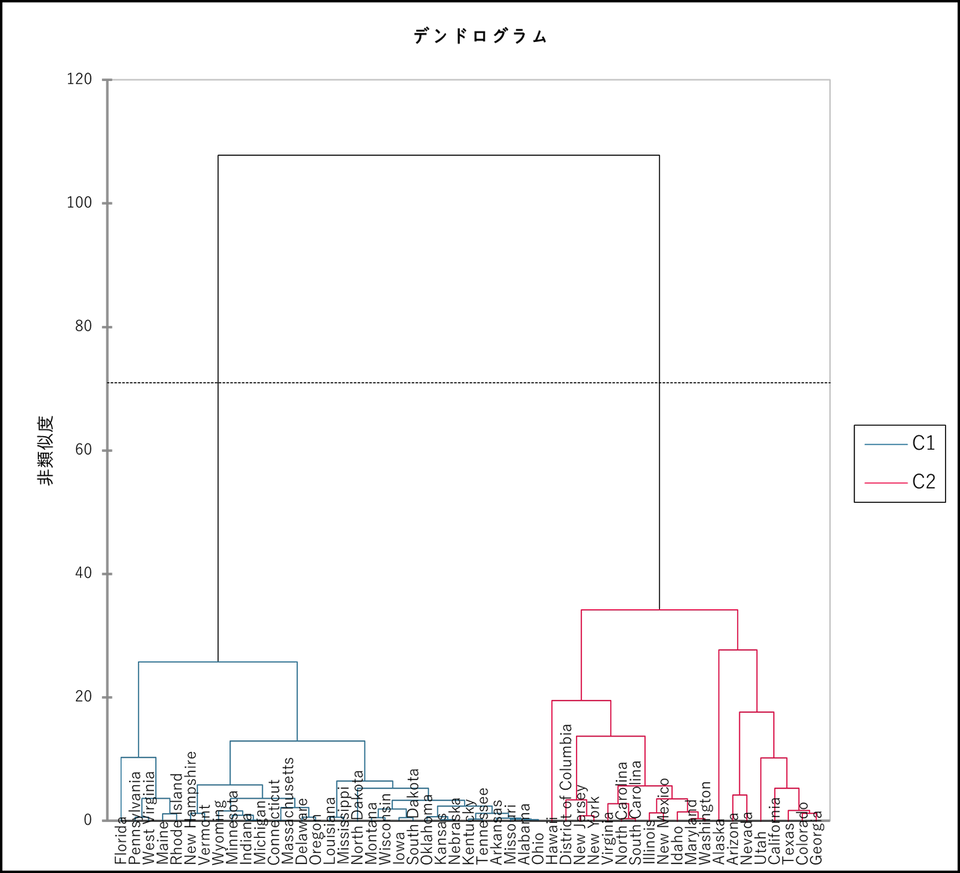
凝集型階層的クラスタリングの結果の見方については下記ページをご参照ください。
Agglomerative Hierarchical Clustering (AHC) in Excel
まとめ
主成分分析は、多数の変数をより少ない変数に置き換え要約することで、データを理解しやすくする分析手法です。XLSTAT を利用することで、簡単な操作で主成分分析を実行し、結果を得ることができます。主成分分析を用いて複数の変数を持つ顧客データを分析することで、顧客の嗜好や購買行動を理解し、より効果的なマーケティング戦略を立案したり、顧客満足度を高める施策を検討する際に役立てることも可能です。
記事執筆:一般社団法人学術・教育総合支援機構 倉山 太一、川﨑 洋平
一般社団法人学術・教育総合支援機構公式HP:https://iaae.jp/
参考文献
- 主成分分析とは
https://www.intage.co.jp/glossary/401/ - Principal Component Analysis (PCA) in Excel
https://help.xlstat.com/6776-principal-component-analysis-pca-excel
※ 本記事はこちらのチュートリアルページをもとに作成しています。記事内で紹介したサンプルデータもこちらからダウンロードすることができます。
XLSTAT の無料トライアル
トライアルでは、最上位パッケージ XLSTAT Advanced に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介した主成分分析はすべてのライセンスでご利用いただけます。
無料トライアルを申し込む*トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。



