• 独立性のカイ二乗検定とは？
• 独立性のカイ二乗検定の分析過程（理論説明）
• カイ二乗検定を実行する際の注意点
• カイ二乗検定を実行するためのデータセット
• カイ二乗検定の操作手順
• カイ二乗検定の結果の解釈
• カイ二乗検定とフィッシャーの正確確率検定の違いについて（補足）
• カイ二乗検定の活用事例
• まとめ
• 参考文献
• XLSTAT の無料トライアル

独立性のカイ二乗検定とは？

独立性のカイ二乗検定は、2つのカテゴリー変数（性別、血液型など、数値で表せない質的なデータ）に関連があると言えるのか否かを判断するために用いられる統計的な手法です。例えば、男女50名ずつに広告案A と広告案B を提示して、どちらが良いかを調査した結果をもとに、性別によって広告案の好みに差があるのかどうかを統計的に判断します。

上記のように2つのカテゴリー変数の組み合わせごとに、該当するデータの数を表形式でまとめたものをクロス集計表といいます。上記事例では男性は広告案A を好み、女性は広告案B を好む傾向があるように思われますが、今回の調査ではたまたまこのような結果が出ただけという可能性も考えられます。

このようにクロス集計表において、行（性別）と列（広告案）が関係しているのかどうかという疑問に答えるのが今回ご紹介する「カイ二乗検定」です。

独立性のカイ二乗検定の分析過程（理論説明）

独立性のカイ二乗検定は以下の手順で分析を進めます。

1. 帰無仮説と対立仮説を設定する

   カイ二乗検定では以下のように仮説を設定します。

   • 帰無仮説: 2つの変数は独立である（関連性はない）。
   • 対立仮説: 2つの変数は独立ではない（関連性がある）。

2. 期待度数を計算する

   クロス集計表における「期待度数」とは「もし2つの変数に全く関係性がなかったとしたら、このセルにはどれくらいの数がくるはずか」という理論的な数のことです。期待度数は以下の順序で求められます。

   ①. 各広告案の合計度数を計算する

   

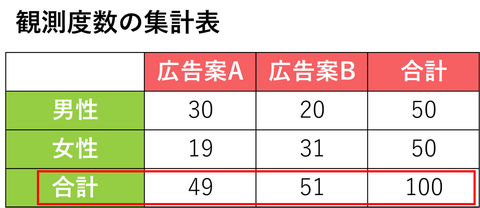
   ②. 合計での構成比率を計算する

   

   ③. 性別で広告案の好みに差がないと仮定したときの度数を合計での構成比率から計算する

   

   男性×広告案A の期待度数：50人×0.49＝24.5件
   男性×広告案B の期待度数：50人×0.51＝25.5件
   女性×広告案A の期待度数：50人×0.49＝24.5件
   女性×広告案B の期待度数：50人×0.51＝25.5件

3. カイ二乗値を計算する

   各セルの期待度数を求めたら、続いてカイ二乗値を計算します。カイ二乗値とは各セルの期待度数と実測値の差（残差）を2乗して、期待度数で割ったものをすべて合計した値のことです。

   

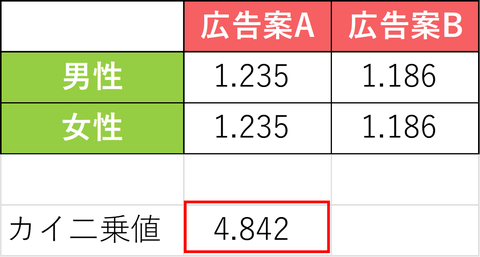
   カイ二乗値の求め方

   ①. 期待度数をもとに相対化した残差をセルごとに計算する
   計算式：(実測値－期待度数) ² ÷期待度数

   男性×広告案A ：(30－24.5) ² ÷24.5＝1.235
   男性×広告案B ：(20－25.5) ² ÷25.5＝1.186
   女性×広告案A ：(19－24.5) ² ÷24.5＝1.235
   女性×広告案B ：(31－25.5) ² ÷25.5＝1.186

   ②. 上記を合計する

   1.235＋1.186＋1.235＋1.186＝4.842

4. 自由度を計算する

   カイ二乗値は2×3 や 4×5 のようにクロス集計表が大きくなると、合計値も大きくなる傾向があります。そこで表の大きさを「自由度」で加味して、カイ二乗値を判断します。自由度は以下の式で計算します。

   自由度＝（行の選択肢の数－1）×（列の選択肢の数－1）

   今回の事例では行数が2（男性、女性）、列数が2（広告案A、広告案B）なので、自由度は (2-1) × (2-1) = 1 となります。
   

5. カイ二乗分布とカイ二乗値を比較して判定する

   カイ二乗分布表で有意水準が5% のときのカイ二乗値を確認し、計算で得られたカイ二乗値と比較します。もし計算したカイ二乗値の方が大きければ、「帰無仮説を棄却し、2つの変数間に関連性がある」と判断します。例えば今回の場合、分布表で自由度「1」、有意水準「0.05」の項目を確認すると、「3.84」となっています。それに対して今回のデータで得られたカイ二乗値は「4.842」であり、分布表のカイ二乗値よりも大きいため、性別と広告案の好みには関連性があると判断します。

   

カイ二乗検定を実行する際の注意点

カイ二乗検定を実行する際には以下の点に注意する必要があります。

• データはカテゴリー変数であること
  独立性のカイ二乗検定は、カテゴリー変数に対して実行します。連続データ（身長、体重、温度など）の場合は、適切なカテゴリー分け（身長なら低、中、高）を行う必要があります。

• 各セルの期待度数は5以上を確保する
  あるセルに含まれる度数があまりに少ないと、少しの度数の変化で比率が大きく変わるため、検定結果の信頼性が低くなることがわかっています。もし5以上の度数を確保することが難しいようであれば、セルを併合したり、フィッシャーの正確確率検定などほかの検定方法を検討する必要があります。

カイ二乗検定を実行するためのデータセット

本ページではキャンペーン中にオンラインショップで買い物をしたユーザー55名を購入金額別に3つのグループ（上位、中位、下位）に分け、購入前に見たキャンペーンの告知（メールニュース、SNS、その両方）を質問した結果をまとめたデータを使用します。

今回はこのデータに対してXLSTAT でカイ二乗検定を行い、購入前に見たキャンペーン告知と購入金額に関連があるのかどうかを確認します。

サンプルデータのダウンロードはこちらから

Chi-Square-Test-Sample-Data.xlsm

なお、XLSTAT ではクロス集計表ではなく、以下のようなリスト形式でもカイ二乗検定を実行することが可能です。

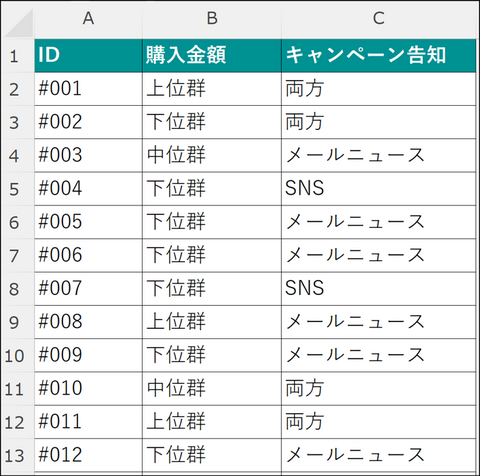
カイ二乗検定の操作手順

1. XLSTAT を起動し、[仮説を検定] > [相関/属性相関の検定] > [分割表での検定（カイ2乗...）] を選択します。

   

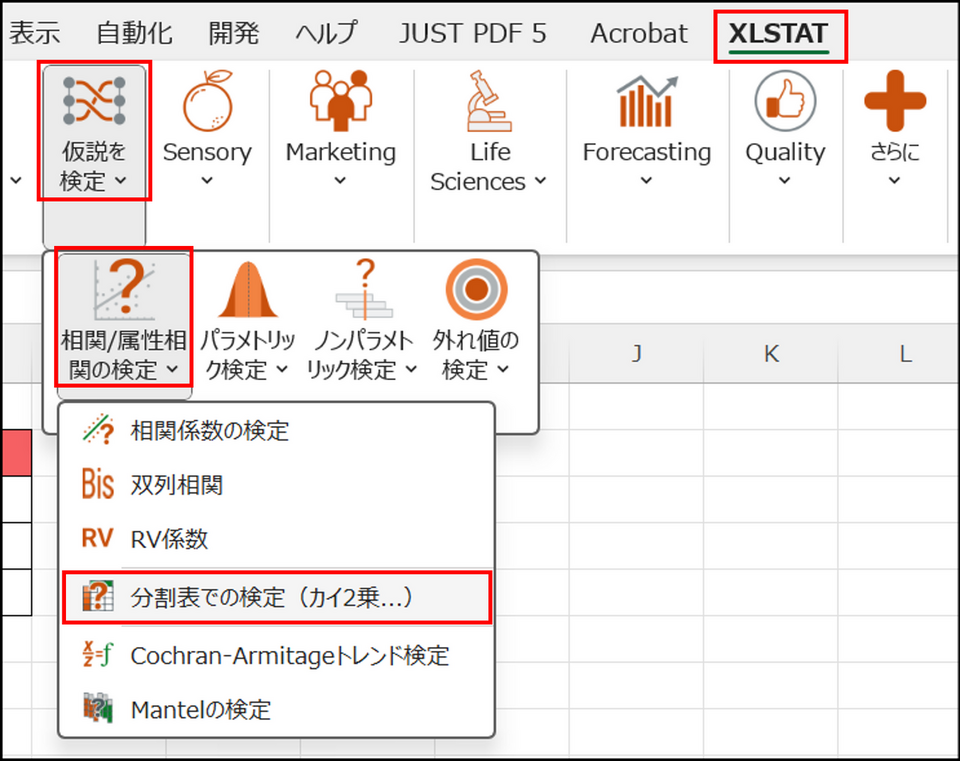
2. ダイアログボックスが表示されるので、下記項目を指定します。

   

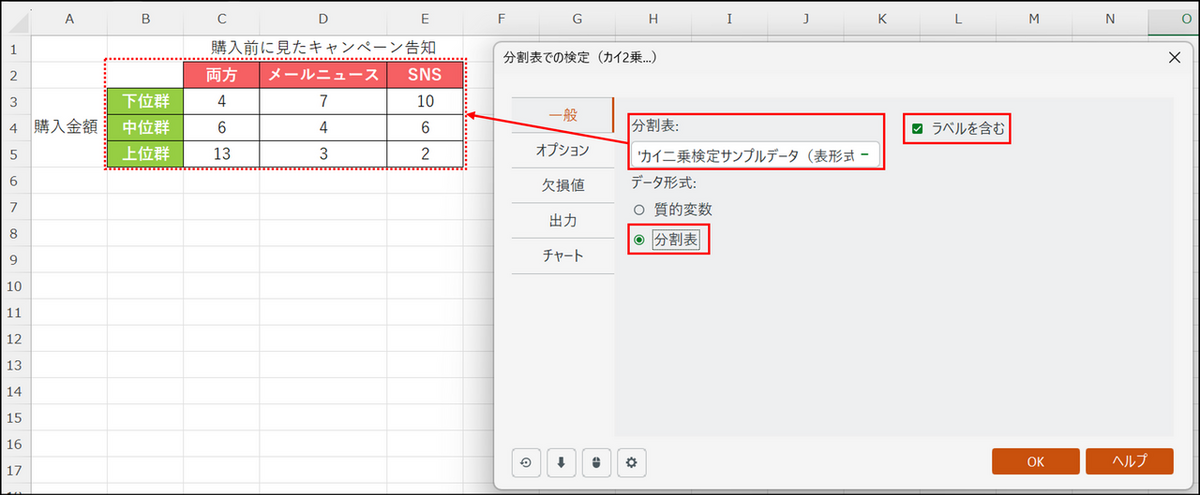
   • データ形式：[分割表] を選択。
   • 分割表：分析対象のデータセルをラベルも含めて直接選択し、[ラベルを含む] の項目にもチェックを入れる。

   ---

   【補足】

   リスト形式のデータの場合は、以下のようにデータを選択します。

   

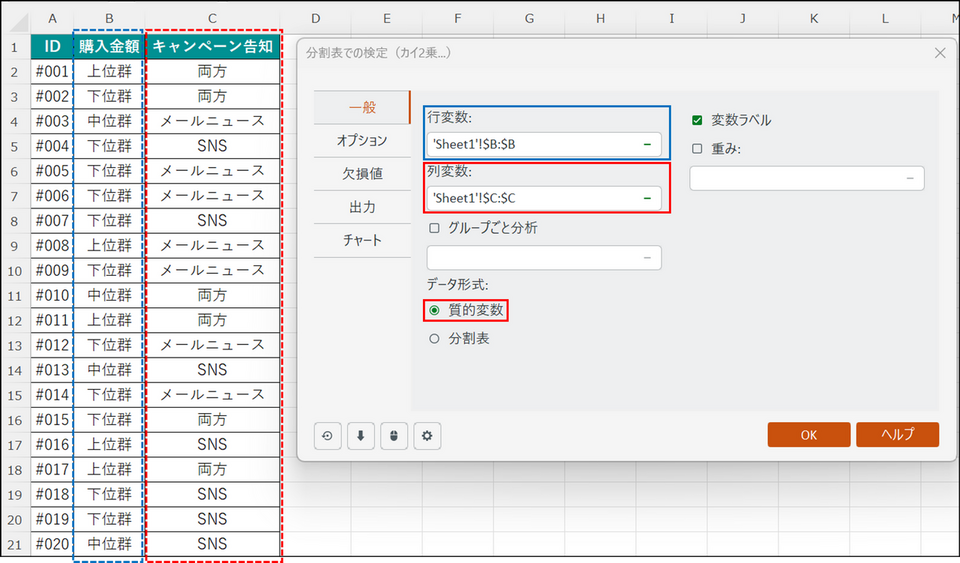
3. [オプション] タブに切り替え、[カイ2乗検定] と[Fisherの正確確率検定] にチェックを入れます。

   

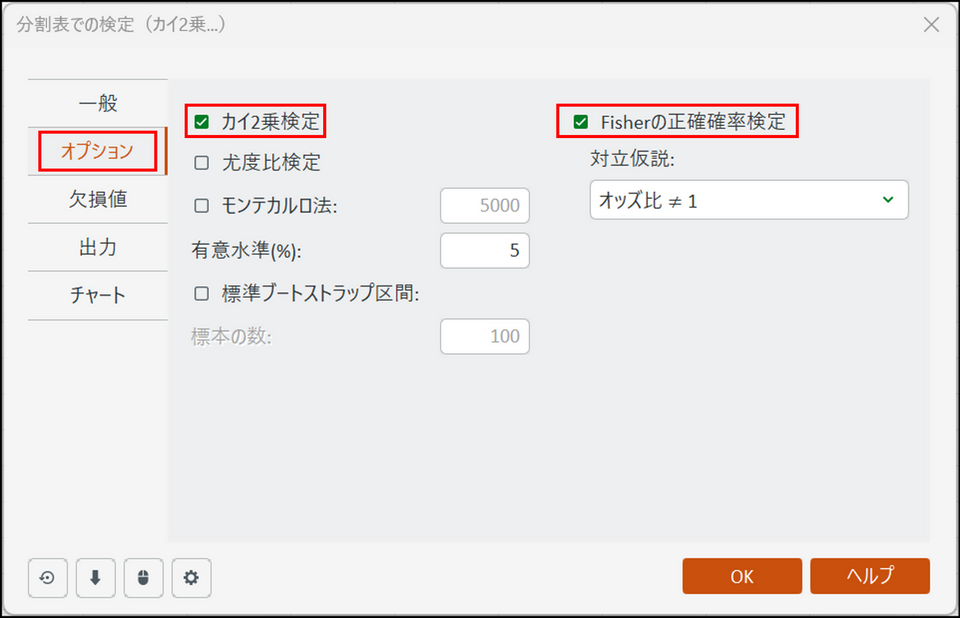
   [Fisherの正確確率検定] の項目にチェックを入れておくことで、フィッシャーの正確確率検定の結果も出力されます。

4. [出力] タブに切り替え、すべての項目にチェックを入れます。

   

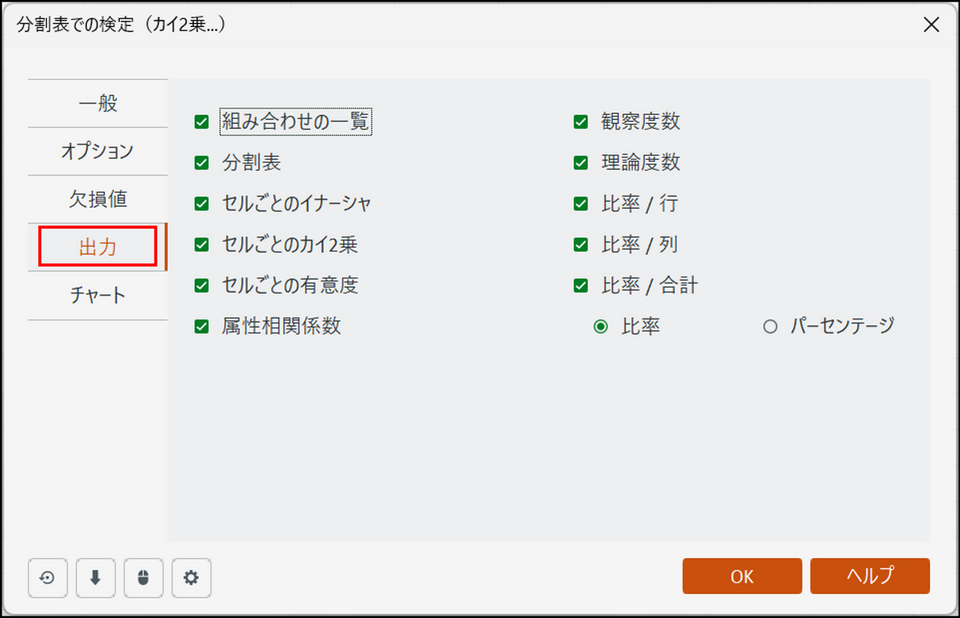
5. [OK] をクリックすると計算が始まり、結果が別シート（属性相関係数）に出力されます。

カイ二乗検定の結果の解釈

行と列の独立性の検定（カイ 2乗）

結果の最初に表示される「行と列の独立性の検定（カイ 2乗）」でp 値を確認します。今回の場合、p 値は0.019 となっています。つまり、「購入金額とキャンペーン告知方法は関連がない」という仮定で、今回のデータが偶然得られる可能性は1.9％であることを示しています。5%有意水準を採用するなら、p 値が0.05 よりも小さいため、「今回のデータから、購入前に見たキャンペーン告知と購入金額に関連がある（有意差あり）」と主張できることになります。

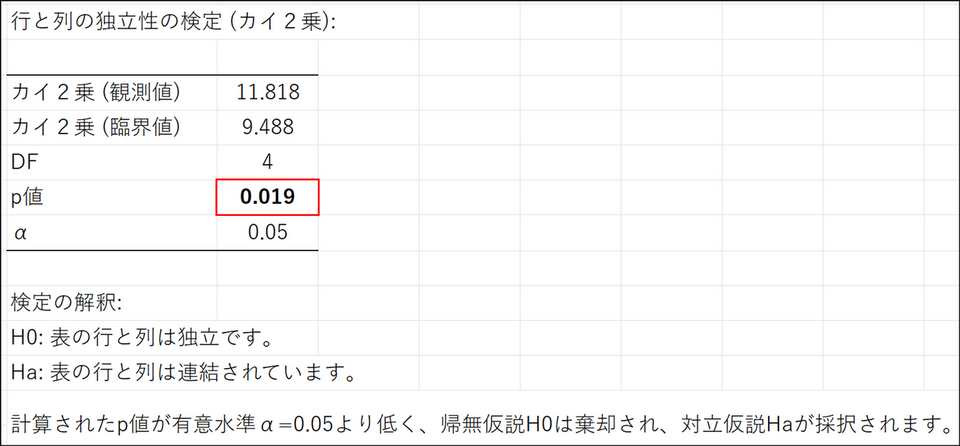
しかし、今回のデータでは期待度数が5未満のセルが2つあります。前述の注意点でも説明した通り、期待度数が5未満のセルがあると、検定結果の信頼性が低くなってしまうため、フィッシャーの正確確率検定の結果も確認します。

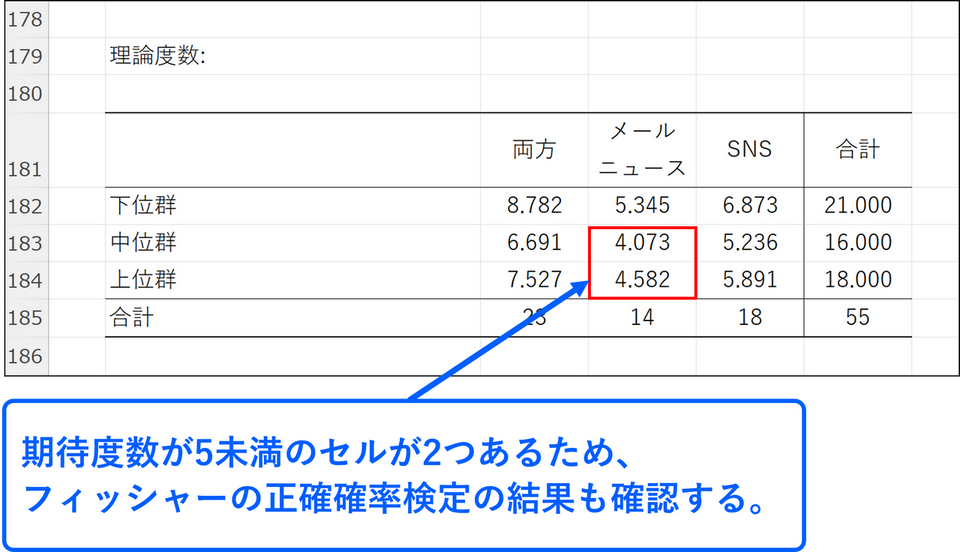
※期待度数（理論度数）の表は結果の下方に表示されます。

Fisher の正確確率検定

フィッシャーの正確確率検定の結果を確認すると、p 値は0.017 で有意水準5％より小さいため、カイ二乗検定の結果と大きな違いはないと判断できます。

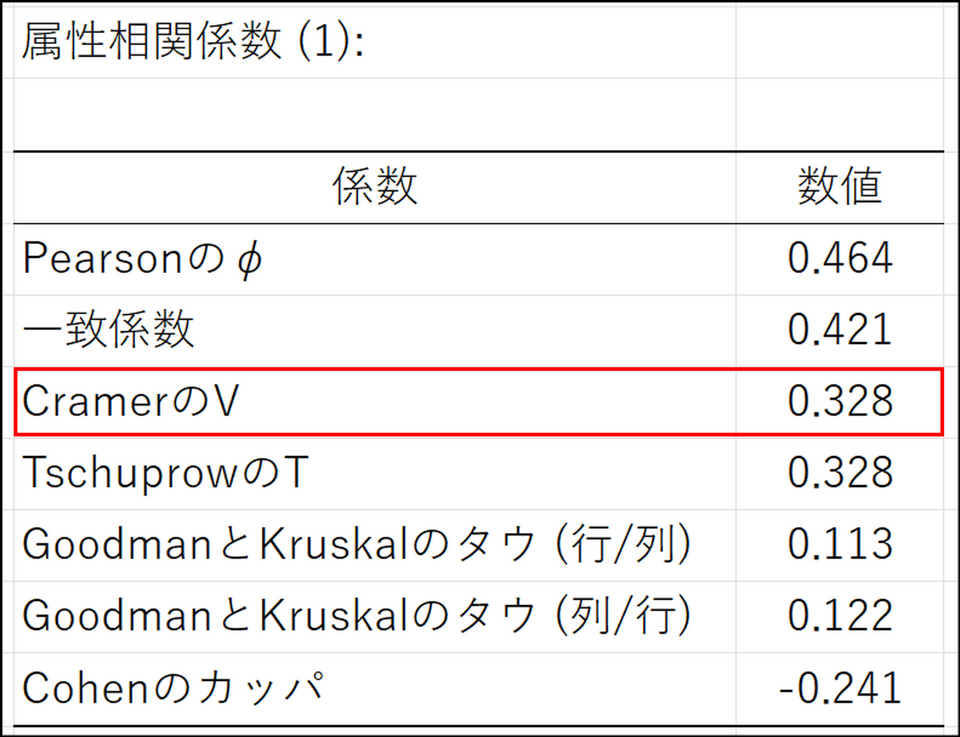
属性相関係数

属性相関係数の表では各種相関係数が表示されます。例えば、CramerのV（クラメールの連関係数）はカテゴリー変数同士の関連度合いを表しており、0～1 の値で出力されます。2変数が強く関連しているほど1に近づき、そうではないほど0 に近づきます。今回の場合、クラメールの連関係数は0.328 なので、中程度の関連がありそうです。

残差 (調整済み)

調整済み残差分析ではクロス集計表の各セルについて、どこに差があるのかを分析することができます。有意差のあるセルは太字で表記されます。

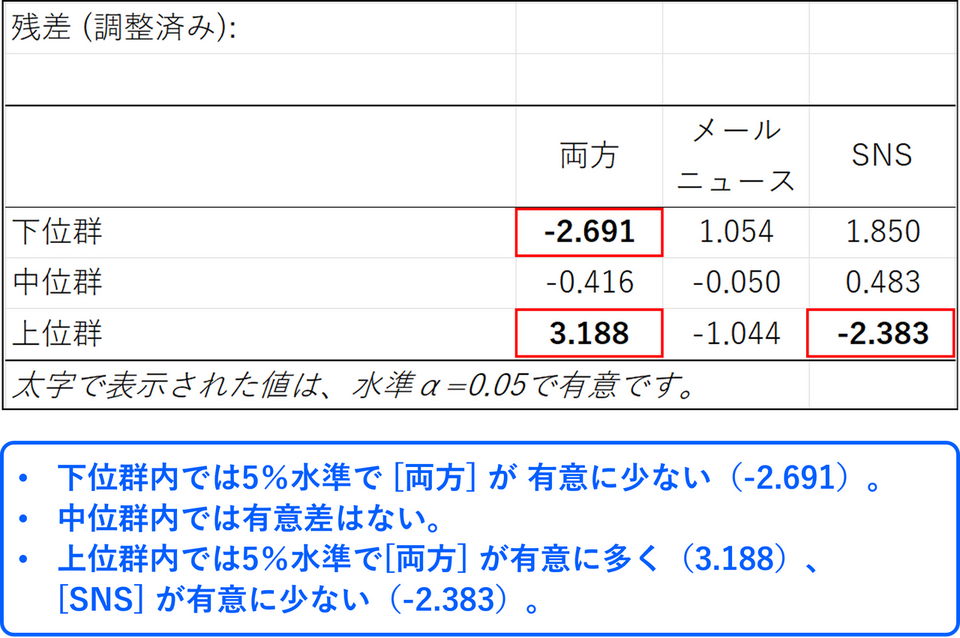
上記の結果から購入前に見たキャンペーン告知と購入金額には比較的強い有意な関連があることが示唆されました（カイ二乗検定のp 値：0.019、フィッシャーの正確確率検定のp 値：0.017、クラメールの連関係数：0.328）。また、残差分析により購入金額の上位群では購入前にSNS だけを見た人数が有意に少なく、メールニュースとSNS の両方を購入前に見た人数がより多い傾向にあることがわかりました。この結果をうまく活用すれば、一人当たりの購入金額を増やすためにどのような施策を打ち出せば良いのかといったヒントを得ることができるかもしれません。

カイ二乗検定とフィッシャーの正確確率検定の違いについて（補足）

カイ二乗検定とフィッシャーの正確確率検定は、どちらも2つのカテゴリ変数の間に関連があるかどうかを調べるために使われる統計検定ですが、以下のような違いがあります。

特徴	カイ二乗検定	フィッシャーの正確確率検定
計算方法	カイ二乗分布を用いてp 値を計算	すべての可能なデータの組み合わせを考慮してp 値を計算
サンプルサイズ	大規模	小規模でも可能
期待度数	5以上が推奨	制限なし
計算量	計算が比較的簡単	サンプルサイズが大きくなると、計算量が膨大になる可能性がある

一般的に、サンプルサイズが大きく、期待度数が十分にある場合はカイ二乗検定で十分な精度が得られます。しかし、サンプルサイズが小さかったり、期待度数が少ない場合は、フィッシャーの正確確率検定の方がより正確な検定結果を得ることができます。

カイ二乗検定の活用事例

このチュートリアルではマーケティング分野での事例をご紹介しましたが、カイ二乗検定はカテゴリー変数を扱うさまざまな分野で利用できます。最後に医学、教育学、心理学分野での活用事例を簡単にご紹介します。

事例1. 医学：新薬の副作用の分析

新薬を投与された患者と標準治療を受けた患者で分類し、副作用の有無を確認。
投与された薬の種類と副作用の有無に関連があるかどうかを検定。

事例2. 教育学：生徒の参加意欲と教授法の関連

教授法により生徒を2つのクラス（講義形式と課題解決型学習）に分け、生徒たちの授業への参加意欲を「高い」「普通」「低い」の3段階で評価。
教授法と生徒の参加意欲に関連があるのかを検定。

事例3. 心理学：色の好みと性格特性の関連性

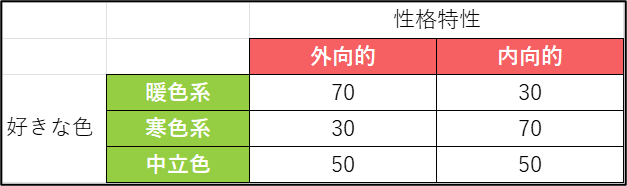
好みの色で回答者を分け、性格特性を測定する尺度を用いてデータを収集。
人が好む色と性格特性（外向的、内向的）に関連性があるのかを検定。

まとめ

カイ二乗検定は、2つのカテゴリー変数間の関係を分析するために使用され、非常に汎用性の高い統計手法です。Excel 単体でも関数を利用することで、カイ二乗検定を実行することはできますが、データ形式をクロス集計表に変更し、期待度数の集計表も自分で作成する必要があるため、少し手間がかかります。XLSTAT を使うと簡単な操作でカイ二乗検定を実行することができ、残差分析の結果も得ることができます。

参考文献

• Run Chi-square and Fisher’s exact tests in Excel
  https://help.xlstat.com/6647-run-chi-square-and-fishers-exact-tests-excel
  
  
• いちばんやさしい、医療統計. フィッシャーの正確確率検定とは？カイ二乗検定との違いをわかりやすく
  https://best-biostatistics.com/contingency/fisher-exact.html
  
  
• 豊田 裕貴: Excelで学ぶ 実践ビジネスデータ分析, オデッセイ コミュニケーションズ, 2023.
  
  
• 平井明代：教育・心理・言語系研究のためのデータ分析　研究の幅を広げる統計手法, 東京図書, 2021.

XLSTAT の無料トライアル

トライアルでは、最上位グレード XLSTAT Premium に加え、3D Plot と LatentClass のオプションもご利用いただけます。本記事で紹介したカイ二乗検定はすべてのライセンスでご利用いただけます。

無料トライアルを申し込む

＊トライアルは登録完了日に開始され、有効期間は14日間です。トライアルを更新または延長することはできません。